-
Raúl RC
el 4/8/17Mediante la relacion de dispersion k=mω2obtienes la frecuencia angular =>180=1,2ω2=>ω=12,25 rad/s
Como la ecuación del MAS tiene esta forma:
x=Asen(ωt+φ0)
En este caso viendo las condiciones iniciales te dicen que en t=0 el sistemas parte de x=0.15, con lo cual parte del extremo superior, lo cual nos indica que tu expresión es coseno, con lo cual:
0,15=0,15cos(ω0+φ0)=>φ0=π/2 rad con lo cual tu expresión quedará como:
x(t)=0,15cos(12,25t+π/2) m
Raúl RC
el 5/8/17Si perdon, no me di cuenta de ese dato, con la velocidad que te dan en t=0,16s sacarias la fase inicial:
con lo cual:
v(t)=Aωsen(ωt+φ0) => -0,8=0,15·12,15sen(12,15·0,16+φ0)
Despejas y obtienes la fase, que será distinta a la que yo te puse en el comentario anterior, sorry
Victor
el 6/8/17El problema no dice que 0,15 metros sea la amplitud.De hecho es imposible que sea la amplitud ya que entonces la velocidad sería cero. El problema da en el momento t = 0,16s tanto la posición como la velocidad. Puedes plantear un sistema de 2 ec. con 2 incognitas para hallar la amplitud A y la fase δ. Con esos 2 datos ya puedes hacer la ec. de la posición.

-
Raúl RC
el 4/8/17Hola! Me encantaría ayudarte, pero no respondemos dudas universitarias que no tengan que ver específicamente con los videos que ya ha grabado como excepcion erl profe. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
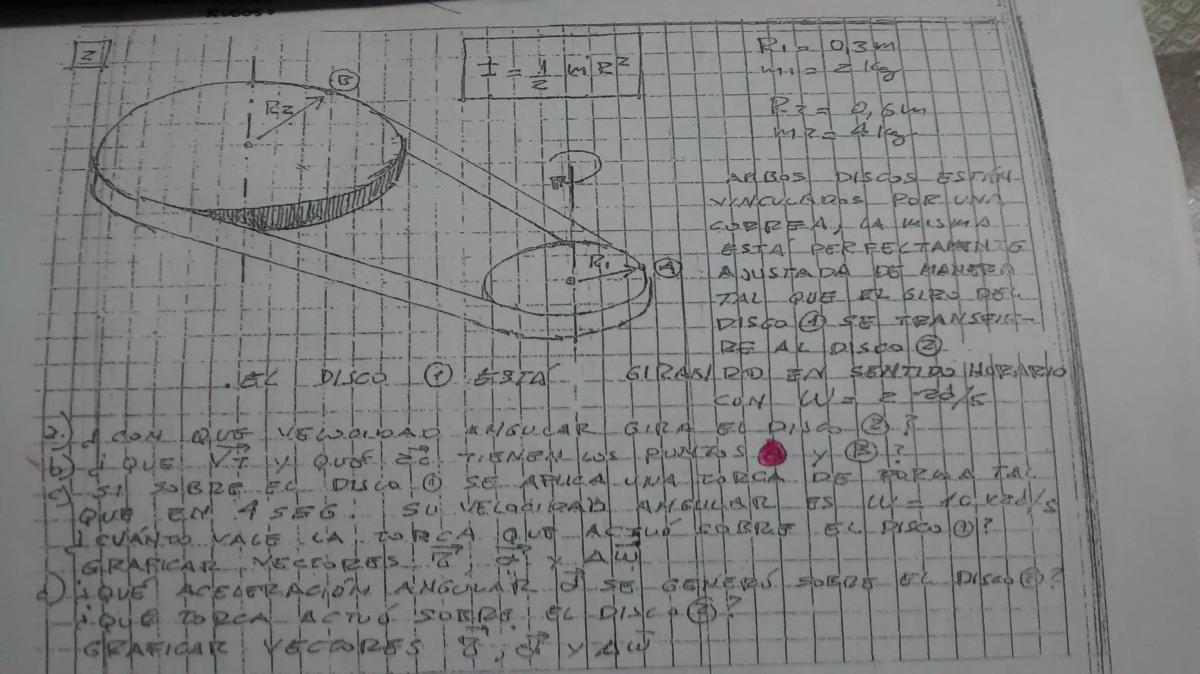
Holaaa!!!, Me pueden ayudar con este problema porque no me da la masa y no logro darme cuenta como plantearlo.
Mediante una soga José arrastra 10 m ( desde una situación A a una situación B) un tronco por el suelo horizontal de un bosque a una velocidad constante de 2.3 m/s. Determine:
a) realice el diagrama de cuerpo libre para el tronco, identificando fuerzas conservativas y no conservativas.
b) ¿cual es el modulo de la tensión de la cuerda?, ¿y el de la fuerza de rozamiento?, ¿ cual es el valor de la aceleración del tronco durante el recorrido?
c) determine el tipo e movimiento realizado por el tronco durante los 10 m de recorrido. Escriba las ecuaciones y graficas del movimiento.
d) variación de energia cinética, variación de energía potencial gravitatoria y variacion de energía mecánica entre A y B. ¿ cual es el valor del trabajo realizado por las fuerzas aplicadas sobre el tronco? ¿ puede estimar el valor de la fuerza resultante sobre el tronco?
e) calcule el trabajo de cada una de las fuerzas no conservativas del ejercicio, si se conoce que el valor absoluto del trabajo realizado por jose es de 589 J.
Raúl RC
el 4/8/17 -
Buenas tardes :) ¿Podéis ayudarme a resolver este problema? Es que no sé cómo plantearlo, muchísimas gracias.
Raúl RC
el 4/8/17Al ser un ejercicio bastante largo te ayudaré con el apartado a)
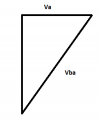
Supongamos que el agua del rio fluye hacia la derecha, con lo cual la barca se verá empujada formando un triángulo rectángulo
El cateto que falta (cuya anchura es D, la correspondiente al río) sería la velocidad obtenida mediante el teorema de pitágoras:
√(vBA2-vA2)
Con lo cual aplicando la expresión de la fórmula del MRU:
v=d/t y teniendo en cuenta que el tiempo que se pide es el de ida y vuelta te quedará que:
t=2D/√(vBA2-vA2)
Espero lo entiendas
-
Podríais ayudarme con este problema? es que me sale un resultado incoherente. Gracias por adelantado!!
-
Antonio Silvio Palmitano
el 3/8/17Puedes plantear que la expresión de la función velocidad es polinómica cuadrática, ya que su gráfica es una parábola:
v(t) = a*t2 + b*t + c, donde tienes que determinar los valores de los coeficientes a, b y c.
Luego, observa que tienes tres valores de la función velocidad en tu enunciado:
v(0) = 0, ya que para t = 0 tienes que la velocidad es nula;
v(-10) = 1000, ya que para t = - 10 s tienes que la velocidad es 1000 cm/s;
v(10) = 1000, ya que para t = 10 s tienes que la velocidad es 1000 cm/s.
Luego, reemplazas valores en la expresión de la función velocidad, y queda el sistema de ecuaciones:
v(0) = 0
v(-10) = 1000
v(10) = 1000;
sustituyess las expresiones de la función velocidad evaluada en los primeros miembros de todas las ecuaciones y queda:
a*02 + b*0 + c = 0
a*(-10)2 + b*(-10) + c = 1000
a*102 + b*10 + c = 1000
resuelves coeficientes, cancelas términos nulos y queda:
c = 0
100*a - 10*b + c = 1000
100*a + 10*b + c = 1000;
reemplazas el valor remarcado en las dos últimas ecuaciones, divides por 10 en todos los términos de dichas ecuaciones y queda:
10*a - b = 100
10*a + b = 100, aquí haces pasaje de término y queda: b = 100 - 10*a (1);
sustituyes la expresión señalada (1) en la primera ecuación y queda:
10*a - (100 - 10*a) = 100, distribuyes en el segundo término y queda:
10*a - 100 + 10*a = 100, haces pasaje de término, reduces términos semejantes y queda:
20*a = 200, haces pasaje de factor como divisor y queda: a = 10;
luego reemplazas en la ecuación señalada (1) y queda: b =100 - 10*10 = 100 - 100 = 0.
Luego, reemplazas los valores de los coeficientes en la expresión de la función velocidad y queda:
v(t) = 10*t2 + 0*t + 0,
cancelas términos nulos y queda:
v(t) = 10*t2.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
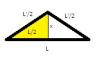
el 3/8/17Observa que el triángulo sombreado en amarillo tiene catetos cuyas longitudes son:
L0/2 y x, y la longitud de su hipotenusa es L'/2;
luego tienes, a partir del Teorema de Pitágoras:
(L0/2)2 + x2 = L'2/2 (1).
Luego, puedes plantear la relación entre la longitud final L' y la longitud inicial L0:
L' = L0*(1 + αΔt),
donde tienes: α = 30*10-6 1/°C, y Δt = 30 °C,
luego reemplazas valores y queda:
L' = L0*(1 + 30*10-6*30),
resuelves el argumento del agrupamiento y queda:
L' = 1,0009*L0 (2).
Luego, solo queda que sustituyas la expresión señalada (2) en la ecuación señalada (1) y despejes la longitud x que te pide el enunciado.
Espero haberte ayudado.