-
 alguien me puede ayudar con el siguiente ejercicios lo he resuelto de la siguiente manera pero aun no sé si lo he hecho bien. muchas gracias
alguien me puede ayudar con el siguiente ejercicios lo he resuelto de la siguiente manera pero aun no sé si lo he hecho bien. muchas gracias Francisco Javier
el 12/8/17Te piden ET/ER:
Como ya mencionas: ET = EL + ER (1)
Dónde:
EL = 0.5*m*v^2
ER = 0.5*I*ω^2
Además:
v= R*ω
I = 0.5*m*R^2
Dividiendo la ecuación (1) entre "ER" quedaría:
ET/ER = EL/ER + 1
Reemplazando para cada energía:
ET/ER = (0.5*m*v^2)/(0.5*I*ω^2) + 1
Y para cada la velocidad y el momento de inercia:
ET/ER = [0.5*m*(R*ω)^2]/[0.5*0.5*m*R^(2)*ω^2] + 1
ET/ER = [0.5]/[0.25] + 1
ET/ER = 2 + 1
ET/ER = 3
-
Antonio Silvio Palmitano
el 11/8/17Observa que tienes tres instantes importantes:
A: la bala está a punto de incrustarse en el cuerpo,
B: la bala recién se incrustó en el cuerpo,
C: el conjunto bala-cuerpo se detiene.
Luego, para cada instante, plantea la cantidad de movimiento (iimpulso) del sistema, y la energía cinética del sistema, con los siguientes datos:
Mb = 100 g = 0,1 Kg, Mc = 38 Kg, μ = 0,12, dBC = 4,2 m.
A)
Observa que el cuerpo está en reposo:
pA = Mb*vb = 0,1*vb;
ECA = (1/2)*Mb*vb2 = (1/2)*0,1*vb2 = 0,05*vb2.
B)
Observa que el conjunto bala-cuerpo se desplaza con rapidez vB.
pB = (Mb + Mc)*vB = (0,1 + 38)*vB = 38,1*vB;
ECB = (1/2)*(Mb + Mc)*vB2 = (1/2)*38,1*vB2 = 19,05*vB2.
C)
El conjunto bala-cuerpo está en reposo.
pC = 0;
ECC = 0.
Luego, observa que entre el instante A y el instante B no actúan fuerzas exteriores al sistema bala-cuerpo en la dirección de movimiento, por lo que puedes plantear que el impulso se conserva:
pA = pB, sustituyes expresiones y queda:
0,1*vb = 38,1*vB, multiplicas por 10 en ambos miembros de la ecuación y queda:
vb = 381*vB (1).
Luego, observa que entre los instantes B y C actúa la fuerza de rozamiento,
cuyo módulo es: fr = μ*(Mb + Mc)*g = 0,12*38,1*9,8 = 44,8056,
y cuyo trabajo queda:
Wfr = - fr*dBC = - 44,8056*4,2 = - 188,18352 J.
Luego, plantea que la variación de energía cinética es igual al trabajo de la fuerza de rozamiento
ECC - ECB = Wfr, sustituyes expresiones y valores y queda:
0 - 19,05*vB2 = - 188,18352, cancelas el término nulo, multiplicas por - 1 en ambos miembros y queda:
19,05*vB2 = 188,18352, haces pasaje de factor como divisor y queda:
vB2 = 9,8784, haces pasaje de potencia como raíz y queda:
vB ≅ 3,1530 m/s, que es la rapidez del conjunto bala-cuerpo en el instante B;
luego reemplazas en le ecuación señalada (1) y queda:
vb ≅ 381*3,1530 ≅ 1197,480 m/s, que es la rapidez de la bala en el instante A.
Observa que entre los instantes A y B no se conserva la energía cinética, porque durante la incrustación de la bala en el cuerpo actúa una fuerza interna de fricción entre la bala y el cuerpo.
Observa que entre los instantes B y C no se conserva el impulso, porque actúa la fuerza de rozamiento ejercida por el piso en la dirección de movimiento, y es una fuerza exterior al sistema bala-cuerpo.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 11/8/17Comienza por establecer un sistema de referencia con eje OX horizontal, con origen en la posición inicial de Romeo, y con sentido positivo hacia la posición inicial de Julieta.
a)
Plantea la ecuación de posición de Movimiento Rectilíneo Uniforme para Romeo, con los datos iniciales:
ti = 0, xi = 0, v = 5 m/s, y queda:
x = 0 + 5*t, cancelas el término nulo y queda:
x = 5*t (1).
Plantea la ecuación de posición de Movimiento Rectilíneo Uniformemente Acelerado para Julieta, con los datos iniciales:
ti = 0, xi = 6 m , vi = 0, a = - 2 m/s2, y queda:
x = 6 + 0*t + (1/2)*(- 2)*t2, cancelas el término nulo, resuelves el coeficiente en el último término y queda:
x = 6 - t2 (2).
Luego, para plantear la condición de encuentro, igualas las expresiones señaladas (1) (2) y queda la ecuación:
5*t = 6 - t2, haces pasajes de términos y queda
t2 + 5*t - 6 = 0, que es una ecuación polinómica cuadrática cuyas soluciones son:
1)
t = - 6 s, que no tiene sentido para este problema;
2)
t = 1 s, que es el instante en que se encuentran Romeo y Julieta,
luego reemplazas en las ecuaciones señaladas (1) (2) y queda:
x = 5*1 = 5 m,
x = 6 - 12 = 6 - 1 = 5 m,
por lo que puedes concluir que la posición de encuentro es x = 5 m.
Espero haberte ayudado.
Antonio Silvio Palmitano
el 11/8/17b)
Observa que las ecuaciones de movimiento para Romeo y para Julieta, respectivamente, son:
x = 5*t
x = 6 + (1/2)*a*t2,
luego igualas expresiones y queda:
6 + (1/2)*a*t2 = 5*t, multiplicas por 2 en todos los términos de la ecuación y queda:
12 + a*t2 = 10*t, haces pasaje de término, ordenas términos y queda:
a*t2 - 10*t + 12 = 0, que es una ecuación polinómica cuadrática, en la que falta determinar el coeficiente a.
Luego, aplicas la fórmula resolvente y tienes las soluciones:
t = ( 10 ± √( (- 10)2 - 4*a*12 ) ) / 2*a = ( 10 ± √( 100 - 48*a) / 2*a,
y recuerda que para que Romeo alcance a Julieta exactamente una vez debe cumplirse que la ecuación tenga una única solución, por lo que el argumento de la raíz cuadrada en la expresión (discriminante) debe ser igual a cero, por lo que plantea:
100 - 48*a = 0, haces pasaje de término y queda:
- 48*a = - 100, haces pasaje de factor como divisor y queda:
a = 25/12 m/s2 ≅ 2,083 m/s2, que es la aceleración máxima que debe tener Julieta para que Romeo la alcance al menos una vez.
Luego, reemplazas en la expresión de las soluciones de la ecuación cuadrática y queda:
t = ( 10 ± √(0) ) / 2*(25/12) = 10 / (25/6) = 60/25 = 12/5 = 2,4 s, que es el instante de encuentro para el caso en que Julieta se desplace con la aceleración máxima cuyo valor hemos remarcado.
Espero haberte ayudado.
Antonio Silvio Palmitano
el 11/8/17c)
Puedes reconstruir el discriminante de la ecuación polinómica cuadrática a partir de la inecuación:
a < 25/12, multiplicas en ambos miembros de la inecuación por - 48 (observa que cambia la desigualdad) y queda:
- 48*a > - 100, sumas 100 en ambos miembros de la inecuación y queda:
100 - 48*a > 0,
por lo que tienes que el discriminante es mayor que cero, y la ecuación cuadrática tiene dos soluciones reales distintas.
Luego, extraes factor común en el primer miembro y queda:
100*(1 - 12*a/25) > 0,
y observa que en el primer miembro tienes que el discriminante es menor que 100,
por lo que su raíz cuadrada es menor que 10, y tienes que las dos soluciones de la ecuación cuadrática son positivas,
y corresponden a dos instantes de encuentro diferentes.
Espero haberte ayudado.
-
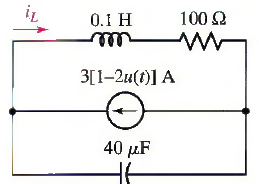
En caso de que alguien sepa. ¿Cómo se calcularía la expresion de corriente en el inductor para todo t? (No tengo problema si usan ecuaciones diferenciales o integrodiferenciales)
Francisco Javier
el 11/8/17Por algún método en específico?
Se puede resolver con un análisis en AC común, frecuencia compleja, Laplace, Fourier, Convolución..
El método más corto y por consiguiente más eficiente, es Laplace. Sin embargo no sé si posees dichos conocimientos.
Cada método tiene una forma bastante diferente de resolución lo cual conlleva a saber conceptos característicos de cada uno.
Por lo tanto, antes de empezar a resolver tendría que saber que tanto sabes, para yo hacerme una idea de con que método entenderías mejor.
Josue Mosh
el 11/8/17Francisco Javier
el 12/8/17Aplicare Laplace.
Se empieza con un análisis para tiempos menores que cero, ya que para este intervalo solo actúa una parte de la fuente de corriente.
Además se debe saber las condiciones del inductor cuando se cambia de intervalo, ya que este no soporta cambios bruscos de corriente, por lo que se puede decir que la corriente del inductor para t- (justo antes del cambio) es igual a la corriente del inductor para t+ (justo después del cambio). Lo mismo para el capacitor; este no soporta cambios bruscos de voltaje, y por lo tanto el voltaje en el capacitor para t- (justo antes del cambio) es igual al voltaje en el capacitor para t+ (justo después del cambio). Además serán necesarios para conocer las fuentes producidas por el inductor y el capacitor en el dominio de Laplace.
Análisis para t<0:
Resulta el siguiente circuito (ver imagen #1).
La fuente de corriente vale 3 A. Como se trata de una fuente DC, el capacitor se vuelve un circuito abierto y el inductor se vuelve un corto circuito.
Primero hallamos la corriente iL. Resulta sencillo, ya que debido a que la rama donde está el capacitor está abierta, no puede circular corriente por allí. Por lo tanto cuando la corriente en la rama donde está la fuente llega al nodo, esta se va toda por la rama donde está la resistencia. Por esta razón:
iL = 3 A
Y por lo tanto: iL(0-) = 3 A = iL(0+)
Y: iL(t) = 3 A
Para el voltaje vc hacemos un recorrido empezando desde el polo positivo, en sentido horario. Resulta:
vc = 100*iL = 100*3 = 300 V
Por lo tanto: vc(0-) = 300 V = vc(0+)
Análisis para t>0:
La fuente de corriente ahora es la suma de dos. La fuente de 3 A más la de 6 A.
Pero ojo con el signo delante de la función escalón. Este signo nos indica que para tiempos mayores a cero la fuente vale - 6 A.
Al ser las dos del mismo tipo (fuentes DC) podemos sumarlas y convertirla en una sola.
Por lo tanto la fuente valdrá 3 - 6 = - 3 A. Este signo negativo implicara la inversión de la fuente de corriente en el circuito.
Entonces resulta el siguiente circuito (ver figura #2). Este circuito está en el dominio del tiempo. Pero resulta que lo queremos en el dominio de Laplace.
Para pasar este circuito al dominio de Laplace, debemos hacer lo siguiente:
- Reemplazar la fuente por su Transformada de Laplace.
- Reemplazar la resistencia por una impedancia que tendrá el valor de R.
- Reemplazar el inductor por una impedancia de valor L*s en serie con una fuente de voltaje o una fuente de corriente en paralelo.
- Reemplazar el capacitor por una impedancia de valor 1/C*s en serie con una fuente de voltaje o una fuente de corriente en paralelo.
Se reemplaza con una fuente de voltaje o corriente dependiendo de cómo te quede después el circuito.
Obviamente se reemplaza para que te quede algo no tan complicado de analizar.
En nuestro caso resulta más conveniente reemplazar el inductor y el capacitor por fuentes de voltajes en serie respectivamente con sus impedancias.
Además, la polaridad de la fuente de voltaje que se reemplaza con el inductor lleva el (-) donde entra la corriente iL. Y para la polaridad de la fuente de voltaje que se reemplaza con el capacitor, esta lleva el (-) en concordancia con el (-) de vc.
El valor de la fuente de voltaje que aparece por el inductor tiene un valor de L*iL(0+). Y el de la fuente que aparece por el capacitor vale vc(0+)/s.
Dicho esto, resulta el siguiente circuito (ver imagen #3). Este circuito está en el dominio de Laplace.
Recuerda que la Transformada de Laplace de una constante "c" es igual a "c/s". Por lo tanto: ℒ{3} = 3/s. Que es lo que aparece en el circuito como fuente.
Ahora nuestro objetivo sera determinar la corriente iL.
Aplicando una ecuación de nodo en "A" nos resulta (repasar Método de Nodos y Transformación de Fuente):
3/250 = (s/25000)*VA + [10/(s+1000)]*VA + 3/(s+1000) + 3/s → VA = [300*(s^2+500*s-250000)]/[s*(s+500)^2]
Por lo tanto: VA = 0.1s*iL - 0.3 → [300*(s^2+500*s-250000)]/[s*(s+500)^2] = 0.1s*iL - 0.3 → iL = [3*(s^2+1000s-250000)]/[s*(s+500)^2]
Hemos encontrado la corriente que deseamos. Sin embargo, esta en el dominio de Laplace. Ahora debemos pasarla al dominio del tiempo.
Aplicamos ahora Transformada Inversa de Laplace. Si expandimos la expresión de la corriente nos queda lo siguiente:
iL = - 3/s + 3000/(s+500)^2 + 6/(s+500)
Para el primer término aplicamos: ℒ-1{c/s} = c.
Dicho esto: - ℒ-1{3/s} = -3.
Para el segundo termino aplicamos: ℒ-1{1/(s-a)^n} = [t^(n-1)*e^(at)]/[(n-1)!]
Dicho esto: 3000*ℒ-1{1/(s+500)^2} = [3000*t^(2-1)*e^(-500*t)]/[(2-1)!] = 3000*t*e^(-500t).
Para el tercer termino aplicamos: ℒ-1{1/(s-a)} = e^(at)
Dicho esto: 6*ℒ-1{1/(s+500)} = 6*e^(-500*t) = 6*e^(-500t).
Finalmente: ℒ-1{iL} = -3 + 3000*t*e^(-500t) + 6*e^(-500t) A = iL(t)
Donde el termino constante es producto de la respuesta forzada y lo demás de la respuesta natural.
iL(t) vale 3 A para t<0 y -3 + 3000*t*e^(-500t) + 6*e^(-500t) A para t>0.
Josue Mosh
el 12/8/17Francisco Javier
el 12/8/17 -
Antonio Silvio Palmitano
el 11/8/17Puedes designar con y0 a la longitud de la barra de aluminio a 0 °C, z0 a la longitud de la barra de hierro a 0 ° C,
yt a la longitud de la barra de aluminio para una temperatura genérica t (distinta de cero), y zt a la longitud de la barra de hierro para una temperatura genérica t (distinta de cero).
Luego, observa que la viga permanece siempre en posición horizontal, por lo que debe cumplirse:
y0 + h = z0, de aquí despejas: y0 = z0 - h (1)
yt + h = zt, de aquí despejas: yt = zt - h (2).
Luego, de acuerdo con la ley de dilatación longitudinal, tienes para cada barra (observa que la variación de temperatura queda: Δt = t -0 °C = t):
yt = y0*(1 + αAl*t) (3)
zt = z0*(1 + αFe*t) (4).
Luego, sustituyes las expresiones señaladas (1) (2) en la ecuación señalada (3) y queda:
zt - h = (z0 - h)*(1 + αAl*t) (5).
Luego sustituyes la expresión señalada (4) en la ecuación señalada (5) y queda:
z0*(1 + αFe*t) - h = (z0 - h)*(1 + αAl*t), distribuyes y queda:
z0 + z0*αFe*t - h = z0 + z0*αAl*t - h - h*αAl*t, haces pasajes de términos y queda:
z0 + z0*αFe*t - h - z0 - z0*αAl*t + h + h*αAl*t = 0, cancelas términos opuestos y queda:
z0*αFe*t - z0*αAl*t + h*αAl*t = 0, divides por t en todos los términos de la ecuación (recuerda que t es distinta de cero) y queda:
z0*αFe - z0*αAl + h*αAl = 0, haces pasajes de términos y queda:
h*αAl = z0*αAl - z0*αFe, extraes factor común en el segundo miembro y queda:
h*αAl = z0*(αAl - αFe), haces pasaje de factor como divisor y queda:
h = z0*(αAl - αFe)/αAl,
luego reemplazas valores y queda:
h = 3,3*(2,2*10-5 - 1,2*10-5) / 2,2*10-5,
resuelves el agrupamiento en el numerador y queda:
h = 3,3*1*10-5 / 2,2*10-5,
simplificas factores, resuelves el numerador y queda:
h = 3,3/2,2 = 3/2 = 1,5 m.
Espero haberte ayudado.
-
En el problema siguiente cómo puedo calcular la energía disipada? Yo creía que era la diferencia entre potencial y cinética pero al ver la solución me he dado cuenta que no es así
Antonio Silvio Palmitano
el 10/8/17Considera un sistema de referencia con un eje de posiciones (alturas) OY vertical, con origen al nivel inicial del tren, y sentido positivo hacia arriba.
a)
Observa que tienes dos instantes importantes:
1) en el nivel más bajo, tienes los datos:
y1 = 0, por lo que la energía potencial inicial queda: EP1 = M*g*y1 = 0,
v1 = 15 Km/h = 15*1000/3600 ≅ 4,167 m/s, por lo que la energía cinética inicial queda: EC1 = (1/2)*M*v12 ≅ (1/2)*2*106*4,1672 = 17361111,111 J;
luego, la energía mecánica inicial queda: EM1 = EP1 + EC1 ≅ 0 + 17361111,111 = 17361111,111 J;
2) en el nivel más alto, tienes los datos:
y2 = 707 m, por lo que la energía potencial final queda: EP2 = M*g*y2 ≅ 2*106*9,8*707 = 13857200000 J,
v2 = 15 Km/h = 15*1000/3600 ≅ 4,167 m/s, por lo que la energía cinética final queda: EC2 = (1/2)*M*v12 ≅ (1/2)*2*106*4,1672 = 17361111,111 J;
luego, la energía mecánica final queda: EM2 = EP2 + EC2 ≅ 13857200000 + 17361111,111 = 13874561111,111 J;
luego, tienes para las variaciones de energía:
ΔEP = EP2 - EP1 ≅ 13857200000 - 0 = 13857200000 J = 1,38572*1010 J;
ΔEC = EC2 - EC1 ≅ 17361111,111 - 17361111,111 = 0;
ΔEM = EM2 - EM1 ≅ 13874561111,111 - 17361111,111 = 13857200000 = 1,38572*1010 J.
b)
Comienza por plantear el módulo de la fuerza de rozamiento: fr = 0,8*M*g = 0,8*2*106*9,8 = 15680000 N,
y luego el trabajo de la fuerza de rozamiento, pero observa que su sentido es opuesto al sentido del movimiento,
y que el tren recorre una distancia d = 62 Km = 62000 m:
Wfr = - fr*d = - 15680000*62000 = - 972160000000 J,
luego, plantea para la energía disipada por acción de la fuerza de rozamiento:
H = - Wfr = - (- 972160000000) = 972160000000 = 9,7216*1011 J.
c)
Comienza por calcular el tiempo que tarda el tren en recorrer la distancia d, y para ello plantea:
v*t = d, haces pasaje de factor como divisor y queda:
t = d/v ≅ 62000/4,167 = 14880 s,
luego plantea para el trabajo realizado por la locomotora (observa que se invierte en variar la energía mecánica del tren y en la energía disipada):
WL = ΔEM + H ≅ 13857200000 + 972160000000 = 986017200000 J,
luego, para la potencia desarrollada por la locomotora tienes:
PotL= WL/t = 986017200000 / 14880 ≅ 66264596,774 W = 66,264596774*106= 66,264596774 MW.
Espero haberte ayudado.
-
¿Me podéis ayudar? La densidad de un líquido desconocido es de 880 Kg/m^3. Expresa el resultado en g/cm^3. ¿Flotará en el agua este líquido? Justifique tu respuesta.
¿Sería (880)(1000)/(1000000) y si es menor a 1g/cm3 flotará en el agua?
Antonio Silvio Palmitano
el 10/8/17Recuerda las equivalencias:
1 Kg =1000 g,
1 m3 = (100 cm)3 = 1000000 cm3.
Luego, tienes para la densidad de masa del líquido:
δ = 880 Kg/m3 = 880 * 1000 g / 1000000 cm3 = 880000/1000000 g/cm3 = 88/100 g/cm3 = 0,88 g/cm3.
Y como el líquido tiene densidad menor que la densidad del agua, flotará sobre ella tal como afirmas.
Espero haberte ayudado.
-
Hola,hay un apartado de un ejercicio de electrónica secuencial que no entiendo, agradecería vuestra ayuda, este es el enunciado:

Mi duda es con el apartado b), yo lo hice de esa manera, pero me da que lo tengo mal, en vez de ZA debería ser QA
También agradecería que me explicárais el tema de set y preset, que quiere decir preset asíncrono?, está bien el circuito?
Gracias
Raúl RC
el 11/8/17Hola! Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya ha grabado como excepcion el profe. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-







































