-
 alguien me podria ayudar con el siguiente problema????????????????????????????? lo necesito porque estoy casi seguro que caerá en mi examen de septiembre . gracias de antemano señores :)
alguien me podria ayudar con el siguiente problema????????????????????????????? lo necesito porque estoy casi seguro que caerá en mi examen de septiembre . gracias de antemano señores :)Antonio Silvio Palmitano
el 8/8/17Recuerda las expresiones para las energías cinéticas, y la relación entre velocidad lineal y velocidad angular:
ECT = (1/2)*M*v2,
ECR = (1/2)*I*ω2,
v = ω*R,
I = (1/2)*M*R2.
Luego sustituyes la tercera expresión en la primera ecuación, y la cuarta expresión en la segunda ecuación, y quedan:
ECT = (1/2)*M*(ω*R)2 = (1/2)*M*ω2*R2,
ECR = (1/2)*(1/2)*M*R2*ω2 = (1/4)*M*R2*ω2,
luego, la energía cinética total queda:
EC = ECR + ECT =(1/2)*M*ω2*R2 + (1/4)*M*R2*ω2 = (3/4)*M*R2*ω2,
luego, la razón entre la energía cinética de rotación y la energía cinética total queda
ECR / EC = ECR / EC = (1/4)*M*R2*ω2 / (3/4)*M*R2*ω2 = simplificas factores = (1/4) / (3/4) = 1/3,
y, recíprocamente, la razón entre la energía cinética total y la energía cinética de rotación queda:
EC / ECR = 3/1 = 3.
Espero haberte ayudado.
-
Ariadna Santana
el 8/8/17
Antonio Silvio Palmitano
el 9/8/171)
Tienes un problema de Movimiento Circular Uniforme.
a)
Tienes la velocidad angular:
ω = 3 rev/s = 3 rev / 1 s = 3 rev / (1/60) min = 3*60 rev/min = 180 rev/min;
ω = 3 rev/s = 3 rev / 1 s = 3*2π rad / 1s = 6π rad/s ≅ 18,8496 rad/s.
b)
θ = ω*t = reemplazas = 6π rad/s * (1/10) s = (6π/10) rad = (3π/5) rad ≅ 1,8850 rad.
c)
v = R*ω = reemplazas = 1 m * 6π rad/s = 6π m/s ≅ 18,8496 m/s (recuerda que el radián es una unidad abstracta).
d)
s = v*t = 6π m/s * (1/10) s = (3π/5) m/s ≅ 1,8850 m.
Espero haberte ayudado.
-
Holaa, necesito ayuda con estos ejercicios profesor, estoy estudiando para el examen de septiembre y se me da muy mal la física, se los agradecería muchisimo!


-
Hola como están? estoy haciendo este ejercicio y no entiendo que es lo que me pide exactamente. pensé que me pedía hallar la identidad , pero en el ejercicio i) me da directamente una identidad fundamental. Si alguien me puede orientar se lo agradecería muchisimo.
Ángel
el 8/8/17Pon tu duda en https://www.unicoos.com/foro/matematicas
Un saludo.
-
Hola! Me podrían dar una mano con este ejercicio?
Dos piraguas parten del reposo y siguen el mismo trazado de competición. La piragua A alcanza la linea de meta en la mitad de tiempo que la B. Suponiendo aceleración constante para ambas embarcaciones, encontrar el cociente entre las aceleraciones de las piraguas A y B.
Debe dar aA/aB =4
No me sale, me esta volviendo loca :(
Gracias..Francisco Javier
el 8/8/17Tomamos origen el lugar de partida.
Ecuación de posición para A: x = xo + vot + 0.5aAtA2
Como parte del reposo, vo = 0.
Como completa la carrera a la mitad del tiempo que B, tA = 0.5tB
Parte del origen, xo = 0.
Aplicando todo esto a la ecuacion planteada nos queda: x = 0 + 0*t + 0.5*aA*(0.5tB)2 → x = 0.125aAtB2
Despejando para "aA" obtenemos: aA = 8x/tB2
Ecuación de posición para B: x = xo + vot + 0.5aBtB2
Como parte del reposo, vo = 0.
Parte del origen, xo = 0.
Aplicando todo esto a la ecuacion planteada nos queda: x = 0 + 0*t + 0.5*aB*tB2 → x = 0.5aBtB2
Despejando para "aB" obtenemos: aB = 2x/tB2Y realizando la division nos queda:aA/aB = 8x/tB2 / 2x/tB2 = 4 -
Hola, recién he comenzado a aprender acerca de la ecuación de la relatividad especial de Einstein, sin embargo, aún me quedan dudas. La masa que está en e=mc2 es la masa invariante o es la masa relativista? En el mundo macroscópico ésto es igualmente aplicable? En una combstión hay pérdida de materia que se convierte en energía? Por último, tengo entendido que la masa inercial es la resistencia a ser movido o a deternerse que aumenta con la masa, pero si un cuerpo lleva velocidad ésta aumenta, no es contradictorio( pues parte de la masa se convertitira en energía)?
-
 Hola profesor, me podrías ayudar a hacer este ejercicio paso a paso? No lo doy entendido 🤦🏻♂️Gracias!!
Hola profesor, me podrías ayudar a hacer este ejercicio paso a paso? No lo doy entendido 🤦🏻♂️Gracias!!Antonio Silvio Palmitano
el 8/8/17Establece un sistema de referencia OXY con eje OX horizontal y sentido positivo acorde al movimiento del cuerpo, y eje OY vertical con sentido positivo hacia arriba.
Luego, observa que sobre el cuerpo actúan cuatro fuerzas, de las que indicamos módulos, direcciones y sentidos:
Fuerza exterior: F = 60 N, con ángulo de inclinación α = 30°, cuyas componentes son: Fx = 60*cos30°, Fy = 60*sen30°,
Rozamiento: fr = μ*N = 0,2*N, horizontal con sentido negativo,
Peso: P = M*g = 20*9,8 = 196 N, vertical hacia abajo,
Acción normal del suelo N, vertical hacia arriba.
Luego, aplicas la Segunda Ley de Newton y tienes el sistema de ecuaciones
Fx - fr = M*a
Fy + N - P = 0,
sustituyes expresiones y valores y queda:
60*cos30° - 0,2*N = 20*a
60*sen30° + N - 196 = 0, de aquí despejas:
N = 196 - 60*sen30° = 196 - 60*0,5 = 196 - 30 = 166 N,
luego sustituyes en la primera ecuación y queda:
60*cos30° - 0,2*166 = 20*a, resuelves el primer miembro y queda:
18,7615 = 20*a, y de aquí despejas: 0,9381 m/s2≅ a,
luego reemplazas en la expresión del módulo de la fuerza de rozamiento y queda:
fr = 0,2*166 = 33,2 N.
Espero haberte ayudado.
-
Un bloque de 200 g se mueve sobre un plano horizontal sin rozamiento con una velocidad de
10 m s-1 y choca con el extremo libre de un resorte de masa despreciable y constante
elástica k = 1500 N m-1, comprimiéndolo.
a) Haga un análisis energético del problema y calcule la compresión máxima del resorte.
b) Determine la velocidad del bloque cuando el muelle se ha comprimido 6 cm. ayudame con este es que no se como hacerlo bien o por lo menos guiarme porfa Antonio o Raul Gracias de antemano.
Antonio Silvio Palmitano
el 7/8/17Tienes los datos iniciales
M = 200 g = 0,2 Kg,
vi = 10 m/s,
k = 1500 N/m,
Δsi = 0 (el resorte está relajado);
y observa que al finalizar tienes:
vf = a determinar,
Δsf = a determinar (el resorte se comprime).
Luego, observa que el movimiento es horizontal, por lo que no tienes variación de energía potencial gravitatoria,
y las energías cinética de traslación y potencial elástica quedan:
a)
ECi = (1/2)*M*vi2 = (1/2)*0,2*102 = 10 J,
EPei = 0,
ECf = 0 (el bloque se detiene),
EPef = (1/2)*k*Δsf2 = (1/2)*1500*Δsf2 = 750*Δsf2.
Luego, por conservación de la energía, plantea
ECf + EPef = ECi + EPei, cancelas términos nulos, sustituyes expresiones y valores, y queda:
750*Δsf2 = 10, haces pasaje de factor como divisor y queda
Δsf2 = 1/75, haces pasaje de potencia como raíz y queda
Δsf = √(1/75) ≅ 0,115470 m = 11,547 cm, que es la máxima compresión que alcanza el resorte.
b)
ECi = (1/2)*M*vi2 = (1/2)*0,2*102 = 10 J,
EPei = 0,
ECf = (1/2)*M*vf2 = (1/2)*0,2*vf2 = 0,1*vf2 a determinar,
EPef = (1/2)*k*Δsf2 = (1/2)*1500*0,062 = 2,7 J.
Luego, por conservación de la energía, plantea
ECf + EPef = ECi + EPei, cancelas términos nulos, sustituyes expresiones y valores, y queda:
0,1*vf2 + 2,7 = 10, haces pasaje de término y queda:
0,1*vf2 = 7,3 J, haces pasaje de factor como divisor y queda:
vf2 = 73, haces pasaje de potencia como raíz y queda
vf = √(73) ≅ 8,544 m/s.
Espero haberte ayudado.
-
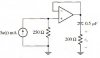
Esta pregunta solo es en caso de que alguien sepa como resolverlo , ¿cómo se sacaría la resistencia equivalente de Thévenin vista desde el capacitor?
Francisco Javier
el 8/8/17Primero debes apagar todas las fuentes independientes presentes en el circuito. Como puedes ver, aquí hay solo una fuente de corriente, por lo tanto la apagamos reemplazándola por un circuito abierto, que es la manera de apagar estas fuentes. Luego, evidentemente la patita (+) del amplificador operacional tendrá un voltaje de cero voltios, debido a que no circula ninguna corriente por la resistencia de 250 Ω. Al tratarse de un amplificador operacional ideal, podemos decir que las patitas de entrada tienen igual voltaje. Quiere decir que la patita (-) también tiene un voltaje de cero voltios. Ahora si quitamos el capacitor y colocamos en su lugar una fuente de prueba "Vp" con el polo (+) mirando al nodo (donde se unen la patita de salida del amplificador con la patita (-) del mismo amplificador y el cable que contiene a la mencionada fuente de prueba y la resistencia de 200 Ω) podremos saber la resistencia que ve esta fuente calculando la relación Vp/Ip, donde "Ip" es la corriente que entrega dicha fuente de prueba. Recuerda que esta corriente debemos colocarla saliendo del polo positivo de la fuente de prueba. Si realizamos un recorrido partiendo del mismo nodo (donde ya dijimos que el voltaje es cero) recorriendo el cable que contiene la fuente de prueba y la resistencia de 200 Ω nos queda lo siguiente (recuerda Kirchhoff):
0 = Vp - 200*Ip
Vp = 200*Ip
Vp/Ip = 200 Ω
La resistencia equivalente de Thevenin vista por el capacitor sería de 200 Ω.
Este análisis se puede omitir casi por completo si conoces el circuito equivalente de un amplificador operacional y sus caracteristicas. Pero como desconozco si posee esos conocimientos pues no enrollo más las cosas.