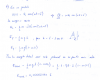-
hola, estoy estudiando fisica para las recuperaciones, y tengo una duda. No entiendo el impulso mecanico, y en uno de los problemas que tengo que hacer dice: "Una pelota de golf de 30 gramos que esta inicialmente en reposo es impulsada por un jugador y coge una velocidad de 104km/h. Aplicando el teorema mecanico estimad cual ha estado la fuerza mediana efectuada sobre la pelota, suponiendo que ha actuado en intervalo de tiempo de 0'07 segundos" y el resultado que me ha dado en el libro es 12'4N
Antonio Silvio Palmitano
el 20/8/17Recuerda las definiciones:
Impulso = (Fuerza aplicada)*(intervalo de tiempo), es una magnitud vectorial, y su ecuación es: J = F*Δt.
Cantidad de movimiento = (Masa)*(velocidad), es una magnitud vectorial, y su ecuación es: p = M*v.
Luego, recuerda la relación entre impulso y cantidad de movimiento:
Impulso = variación de la cantidad de movimiento, y la ecuación correspondiente es:
J = pf - pi (1).
Observa que tienes en tu enunciado:
vi = 0 (la pelota está inicialmente en reposo),
vf = 104 Km/h = 104*1000/3600 ≅ 28,889 m/s (la pelota sale impulsada por el golpe del palo de golf),
M = 30 g = 0,03 Kg (masa de la pelota),
Δt = 0,07 s (intervalo de tiempo en que el palo de golf estuvo en contacto con la pelota),
Fm = a determinar (fuerza media ejercida por el palo de golf sobre la pelota).
Luego, plantea la ecuación señalada (1):
J = pf - pi, sustituyes expresiones y queda:
Fm*Δt = M*vf - M*vi, extraes factor común en el segundo miembro y queda:
Fm*Δt = M*(vf - vi), haces pasaje de factor como divisor y queda:
Fm = M*(vf - vi)/Δt,
y solo queda que reemplaces valores y hagas el cálculo del módulo de la fuerza media aplicada sobre la pelota.
Espero haberte ayudado.
-
hola, tengo una duda, en el ejercicio me pone: un astronauta de 80 kg queda aparado en el espacio a 30 m de su nave. A fin de retornar a ella, lanza una llave de 0.5 kg con una rapidez de 20 m-s en sentido opuesto a donde se encuentra la nave. ¿Con que velocidad(vectorial) volverá a la nave? ¿cuanto tiempo tardará en llegar a ella, suponiendo movimiento uniforme?. He visto los videos pero no me sale ninguno de este tipo. no se como calcular lo que me pide y tampoco como poder hacer un dibujo aclarativo. un saludo
Joan Carricondo
el 20/8/17Hola clara, me da esto de resultado:
Velocidad con la que vuelve a la nave= 0,125m/s
Tiempo que tarda en llegar a la nave= 240s
Para resolverlo he usado las formulas: m1×v1+m2×v2=m1×v1'+m2×v2'
Sustituyo: 80×v1+0,5×20=80×0+0,5×0
Aislas la v1 y te da la velocidad del astronauta.
Despues sustituyes en la formula: x=x'+v×t que seria 30=0+0,125×t aislas la t y da el tiempo que tarda.
Las que lleban el simbolo ' es porque son los iniciales.
Espero haberte ayudado, creo que esta bien resuelto.
-
hola buenas noches ,es que calcule cuanto se desintegraria un 90% de 28 mg de yodo l-131 y me dio que 26,7 dias. pero la vida media de ese isotopo es de 8,0197 dias alguien me hace el favor de aclararme esa duda.
Antonio Silvio Palmitano
el 20/8/17Puedes plantear una tabla de valores tiempo (t) - masa remanente (y):
t y
0 28
8,0197 14
a determinar 2,8
Luego, plantea el modelo exponencial:
y = 28*ek*t (1),
luego sustituyes los dato correspondientes al tiempo de vida media y queda la ecuación:
14 = 28*ek*8,0197, haces pasaje de factor como divisor y queda:
0,5 = ek*8,0197, compones en ambos miembros con la función inversa de la función exponencial natural y queda:
ln(0,5) = k*8,0197, haces pasaje de factor como divisor y queda:
ln(0,5)/8,0197 ≅ -0,0864 ≅ k;
luego reemplazas en la ecuación señalada (1) y queda:
y = 28*e-0,0864*t.
Luego sustituyes la expresión de la masa remanente y queda:
2,8 = 28*e-0,0864*t, haces pasaje de factor como divisor y queda:
0,1 = e-0,0864*t, compones en ambos miembros con la función inversa de la función exponencial natural y queda:
ln(0,1) = - 0,0864*t, haces pasaje de factor como divisor y queda.
- ln(0,1)/0,0864 ≅ 26,6409 días = t.
Por lo que veo, has obtenido la respuesta correcta.
Espero haberte ayudado.
-
Buenos días, ¿alguien puede ayudarme a plantear este ejercicio? Gracias de antemano y saludos desde Madrid.
Determine la cantidad de agua a 20 o C que se necesita echar en una olla para conseguir que rompa a hervir exactamente en 5 minutos, si empleamos una cocina que tiene 2 kW de potencia calorífica y el rendimiento de la cocina es del 40 %
Antonio Silvio Palmitano
el 20/8/17Observa que empleamos el Sistema Internacional de Unidades de Medida (recuerda el equivalente mecánico del calor: 1cal ≅ 4,184 J).
Comienza por plantear la cantidad de calor que se debe entregar a la masa de agua para que alcance su temperatura de ebullición:
ΔQ = M*ce*ΔT = M*( 1000 cal/(Kg*°C) )*(100 °C - 20°C) = M*1000*80 cal/Kg = M*80000 cal/Kg ≅ M*80000*4,184 J/Kg = M*334720 J/Kg.
Luego,calcula la potencia efectiva:
Potef = 0,40*2 KW = 0,8*1000 W = 800 W.
Luego, plantea la relación entre potencia y energía entregada en forma de calor:
ΔQ/Δt = Potef, haces pasaje de divisor como factor y queda (observa que expresamos el intervalo de tiempo en segundos):
ΔQ = Potef*Δt, sustituyes expresiones y queda:
M*334720 J/Kg = 800 W * 300 s, haces pasaje de factor como divisor y queda:
M = 240000/334720 Kg ≅ 0,717 Kg.
Espero haberte ayudado.
-
Hola, tengo el siguiente enunciado.
Una bala de 15 g que va a una velocidad de 450m/s atraviesa un tablón de 7cm de amplio, suponiendo que el tablón tiene una fuerza resistente de 1800N.
Calcula a que velocidad sale la bala del tablón.Si alguien me puede ayudar a resolverlo, muchas gracias.
Antonio Silvio Palmitano
el 20/8/17Tienes que la bala recorre una longitud L = 7 cm = 0,07 m dentro del tablón, que ejerce sobre ella una fuerza de rozamiento opuesta a la dirección de movimiento, cuyo módulo es fr = 1800 N.
Luego, establece un sistema de referencia con un eje de posiciones OX con dirección y sentido positivo acordes al movimiento de la bala,
luego planteas la relación entre el trabajo de la fuerza de rozamiento y la variación de la energía cinética de la bala:
ECf - ECi = Wfr, sustituyes expresiones y queda:
(1/2)*Mb*vf2 - (1/2)*Mb*vi2 = - fr*L,
multiplicas en todos los términos por 2/Mb y queda:
vf2 - vi2 = - 2*fr*L/Mb, haces pasaje de término y queda:
vf2 = vi2 = - 2*fr*L/Mb,
luego, solo queda que reemplaces valores y despejes el módulo de la velocidad de la bala al salir del tablón.
Espero haberte ayudado.
-
Raúl RC
el 21/8/17Hola! Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Necesito ayuda con un problema de solido-rigido relacionado con el momento de inercia e velocidad angular,les dejo el enunciado.Dos niños de 25 kg cada uno están en los extremos opuestos de una plancha cuadrada horizontal de 2.6 m de largo y 10 kg de masa, y rotan a 5 rpm con respecto a un eje que pasa por su centro. a) ¿Cuál sería la velocidad angular si cada niño se acerca al centro 60 cm? b) ¿Cuál será el cambio en la energía cinética? Dato Iplaca=mpL/6
Antonio Silvio Palmitano
el 19/8/17Puedes plantear el impulso angular inicial:
Mi = Ip*ωi + 2*In*ωi = (Mp*L2/6 + 2*Mn*(L/2)2)*ωi = (Mp*L2/6 + 2*Mn*L2/4)*ωi = (L2/2)*(Mp/3 + Mn)*ωi (1).
Tienes los datos:
L = 2,6 m, Mp = 10 Kg, Mn = 25 Kg, ωi = 5 rev/min = 5*2π rad / 60 s = (π/6) rad/s,
por lo que puedes calcular el módulo del impulso angular inicial.
Puedes plantear el impulso angular final:
Mf = Ip*ωf + 2*In*ωf = (Mp*L2/6 + 2*Mn*x2)*ωf (2).
Tienes los datos:
L = 2,6 m, Mp = 10 Kg, Mn = 25 Kg, ωi = 5 rev/min = 5*2π rad / 60 s = (π/6) rad/s, x = L/2 - 60 cm = 1,3 m - 0,6 m = 0,7 m, ωf = a determinar.
por lo que puedes plantear el módulo del impulso angular final.
Luego, como no actúan momentos de fuerzas exteriores al sistema plancha-niños, puedes plantear conservación del impulso angular, igualas las expresiones señaladas (1) (2) y queda la euación:
Mf = Mi, sustituyes expresiones y queda la ecuación:
(Mp*L2/6 + 2*Mn*x2)*ωf = (L2/2)*(Mp/3 + Mn)*ωi,
y solo queda que reemplaces valores numéricos y despejes la incógnita remarcada.
Luego, puedes plantear las energías cinéticas de rotación inicial y final:
ECRi = (1/2)*Ip*ωi2 + 2*(1/2)*In*ωi2 = (1/2)*(Mp*L2/6 + 2*Mn*L2/4)*ωi2 (3),
ECRf = (1/2)*Ip*ωf2 + 2*(1/2)*In*ωf2 = (1/2)*(Mp*L2/6 + 2*Mn*x2)*ωf (4),
observa que tienes todos los datos necesarios para calcular las energías, para luego plantear la variación:
ΔECR = ECRf - ECRi.
y solo queda que hagas los cálculos.
Espero haberte ayudado.