-
Se tienen dos cargas Q2= +Q y Q1= -3Q ¿Cual es la nueva magnitud de la carga Q1 si se le agrega la mitad de la carga de Q2?
Q1= -3Q
Q2=Q
Luego, se extrae la mitad de Q2, entonces:
Q1´= -3Q+Q/2
Q2´= Q/2
Alguien me dice si el razonamiento es correcto
-
Hola! Disculpen la molestia quería consultar el punto 1 como resolverlo ya que es un ejercicio de Arquímedes pero se resuelve mediante dinámica, la respuesta final es 60 kg de concreto.
Desde ya muchas gracias y saludos.
-
Hola!
Disculpe, estoy perdido en tema muy fácil, mire quisiera saber como se podía hacer para pasar un numero que digamos puede ser 6,66666 a que pase a 7.
Me perdí en eso ya que lo vi hace mucho y me confundí demasiado.
Muchas Gracias!
Gonzalo Blanc
el 24/8/17Ese tema creo que se llama truncado
6,0≅ 6
6,1≅ 6
6,2≅ 6
6,3≅ 6
6,4≅ 6
6,5≅ 6
6,6≅ 7
6,7≅ 7
6,8≅ 7
6,9≅ 7
Cuando tenes un 0, 1, 2, 3, 4 y 5 después de la coma el número se mantiene y cuando tenes un 6, 7, 8, 9 después de la coma el número se puede redondear a 7, espero haberte ayudado según recuerdo es así. Si estoy equivocado corrijanmen !
Gonzalo Blanc
el 24/8/17Sol
el 24/8/17Ángel
el 24/8/17Gonzalo Blanc, corregimos:
Cuando tenes un 0, 1, 2, 3, 4
y 5después de la coma el número se mantiene y cuando tenes un 5,6, 7, 8, 9 después de la coma el número se puede redondear a 7Por lo tanto:
6,0≅ 6
6,1≅ 6
6,2≅ 6
6,3≅ 6
6,4≅ 6
6,5≅
6----- lo correcto es ----> 6,5≅ 76,6≅ 7
6,7≅ 7
6,8≅ 7
6,9≅ 7
-
Hola me podriais ayudar con el siguiente ejercicio:
Una vagoneta de una montaña rusa lleva una velocidad de 4 m/s cuando inicia la bajada por una rampa de 15m de altura. A continuacion, entra en un circulo vertical (loop) de 4m de radio. Calcula la velocidad en el punto pas alto de el "loop", considerando que no hay friccion.
Gracias.Antonio Silvio Palmitano
el 23/8/17Establece un sistema de referencia con un eje de posiciones (alturas) OY con sentido positivo hacia arriba y origen al nivel del punto más bajo del "loop".
Luego, tienes dos instantes importantes: cuando la vagoneta se encuentra en el punto de partida (A), y cuando la vagoneta alcanza el punto más alto del "loop" (B), y observa que indicamos alturas y velocidades para ambos puntos, para luego calcular sus energías potencial gravitatoria y cinética de traslación:
A)
yA = 15 m, vA = 4 m/s;
EPA = M*g*yA,
ECA = (1/2)*M*vA2;
B)
yB = 8 m (dos radios del "loop" por encima del suelo), vB = a determinar;
EPB = M*g*yB,
ECB = (1/2)*M*vB2.
Luego, como tienes en el enunciado que no hay fricción, puedes plantear conservación de la energía mecánica:
EPB + ECB = EPA + ECA, sustituyes expresiones y queda:
M*g*yB + (1/2)*M*vB2 = M*g*yA + (1/2)*M*vA2, multiplicas en todos los términos de la ecuación por 2/M y queda:
2*g*yB + vB2 = 2*g*yA + vA2, haces pasaje de término y queda:
vB2 = 2*g*yA + vA2 - 2*g*yB,
y solo queda que reemplaces valores y despejes el módulo de la velocidad en el punto más alto del "loop".
Espero haberte ayudado.
-
Buenos días les quiero consultar si me pueden ayudar con el punto C del siguiente ejercicio:

Haber, para hacerlo más sencillo, lo que tendría que hacer es: ¿ sacar por separado las resultantes de las dos fuerzas y restarlas ?
Si esto se resolvería como dije en la pregunta así tengo que aplicar esta formula:
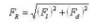 , tomando de referencia las componentes en X y en Y de cada vector para poder hallar las resultantes de cada fuerza.
, tomando de referencia las componentes en X y en Y de cada vector para poder hallar las resultantes de cada fuerza.Antonio Silvio Palmitano
el 23/8/17Comienza por plantear las componentes de cada fuerza:
F1x = F1*cosα1 = 8*cos(60°) = 4 Kgf,
F1y = F1*senα1 = 8*sen(60°) ≅ 6,928 Kgf,
luego, el vector F1 queda expresado:
F1 ≅ < 4 , 6,928 >;
F2x = F2*cosα2 = 5*cos(-53°) ≅ 3,009 Kgf,
F2y = F2*senα2 = 5*sen(-53°) ≅ -3,993 Kgf,
luego, el vector F1 queda expresado:
F2 ≅ < 3,009 , -3,993 >.
a)
Plantea para la fuerza resultante de sumar ambas fuerzas:
Rs = F1 + F2 ≅ < 4 , 6,928 > + < 3,009 , -3,993 > = < 7,009 , 2,935 >,
por lo tanto sus componentes son:
Rsx ≅ 7,009 Kgf, Rsy ≅ 2,935 Kgf.
b)
El módulo de la fuerza resultante de la suma queda:
|Rs| ≅ √(Rsx2 + Rsy2) = √(7,0092 + 2,9352) = √(57,740) = 7,599 Kgf.
c)
Plantea para la fuerza resultante de la diferencia entre ambas fuerzas:
Rd = F1 - F2 ≅ < 4 , 6,928 > - < 3,009 , -3,993 > = < 0,991 , 10,921 >,
por lo tanto sus componentes son:
Rdx ≅ 0,991 Kgf, Rdy ≅ 10,921 Kgf.
El módulo de la fuerza resultante de la diferencia queda:
|Rd| ≅ √(Rdx2 + Rdy2) = √(0,9912 + 10,9212) = √(120,250) = 10,966 Kgf.
Espero haberte ayudado.
-
¿Me podéis ayudar con este ejercicio? Solo tengo una duda....
¿Qué fuerza hay que ejercer para levantar una piedra de 150 Kg con una palanca de 3 m de largo, cuyo fulcro está a 50 cm de la piedra?
Mi problema es, ¿Los 150 Kg lo tendría que pasar a N con la fórmula P=m*g?
Lo otro entiendo que 2,5 será Br y 0,05 será Bp y que habrá que calcular la potencia.
Antonio Silvio Palmitano
el 23/8/17Si trabajas con el Sistema Internacional de Unidades de Medida, tienes los datos:
R = 150*9,8 = 1470 N (resistencia a equilibrar),
bR = 50 cm = 0,5 m (brazo de resistencia),
bP = L - bR = 3 - 0,5 = 2,5 m (brazo de potencia),
P = a determinar (fuerza equilibrante).
Luego, plantea la condición de equilibrio:
P*bP = R*bR, haces pasaje de factor como divisor y queda:
P = R*bR/bP = 1470*0,5/2,5 = 294 N.
Espero haberte ayudado.
-
Buenos días, quisiera saber si me pueden dar una mano con el problema 11. Muchas gracias! Y disculpen las molestias

Guillermo Suárez
el 24/8/17Hola Albano. Este ejercicio va sobre la ley de Snell.
Suponemos que el rayo luminoso entra desde el vacío ( n1 = 1 ) en el plástico, con índice de refracción desconocido n2.
Teniendo en cuenta que:
y que n2 = c / v, siendo v la velocidad con la que se propaga la luz en el plástico, ya sólo te queda hacer el cálculo como un movimiento rectilíneo uniforme: velocidad = espacio recorrido (por trigonometría) / tiempo.
El cálculo es bastante sencillo a partir de aquí, y te agradecería que lo compartieras con el resto de compañeros tú mismo.
Muchas gracias!!
Un saludo,
Guillermo
-
Hola!!
Me podéis decir si este ejercicio está bien resuelto?
Un muelle con una constante de elasticidad de 75 N/m se ha alargado 4 cm.
a) ¿Qué fuerza hemos ejercido para estirarlo?
b) Si lo estiramos con una fuerza de 6 N, ¿Cuántos centímetros se alargará?
Antonio Silvio Palmitano
el 23/8/17Recuerda la ecuación correspondiente a la Ley de Hooke (indicamos los módulos de la fuerza aplicada y del estiramiento o compresión del muelle):
F = k*Δs.
Luego, tienes los datos:
k = 75 N/m (constante elástica del muelle),
a)
Δs = 4 cm = 0,04 m (estiramiento),
luego reemplazas en la ecuación y queda:
F = 75*0,04 = 3 N;
b)
F = 6 N (fuerza aplicada),
luego reemplazas en la ecuación y queda:
6 = 75*Δs, haces pasaje de factor como divisor y queda
0,08 m = Δs.
Espero haberte ayudado.
Carmen
el 23/8/17Antonio Silvio Palmitano
el 23/8/17La ecuación que empleamos es: F = k*Δs porque indicamos solo los módulos, tanto de la fuerza como del estiramiento.
La ecuación de la Ley de Hooke es tal como dices: F = - k*Δs,
y el signo indica que el sentido del vector fuerza es opuesto al sentido del vector estiramiento,
pero los módulos son tales como los hemos calculado.
Espero haberte ayudado.
-
¡Hola unicoos!
Espero me puedan ayudar con un consejo para poder realizar lo siguiente:
Me solicitaron que hiciera una maqueta con el círculo unitario y con este tengo que graficar el seno, coseno y tangente. No tiene que ocupar mucho espacio, algo pequeño.
Ojalá me puedan dar algunas ideas, muchas gracias y saludos. -
HOLA, NECESITO AYUDA URGENTE !!!!! SOBRE FISICA CUANTICA ...LOS PUNTOS SON LOS SIGUIENTES: (DESDE YA MUCHAS GRACIAS)
c.- Así como el límite clásico de la relatividad se puede lograr dejando c → ∞, el límite clásico del comportamiento cuántico
se logra dejando h → 0. Considere lo siguiente ( en el límite h → 0) y explique cómo se comportan clásicamente:
el tamaño del cuanto de energía de una onda electromagnética, la longitud de onda de Broglie de un electrón, las relaciones de incertidumbre de Heisenberg.
d.- Supongamos que una partícula está en el estado fundamental (n = 1) de un pozo de energía potencial finito. La energía es ()2/2mL2 = K + U =K; por lo tanto (
)2/2mL2 =K (Lo que no se nota es ¿Cuánto vale K en función de px?De este valor de K, despejar px.Así si px es exactamente conocido, entonces Δpx = 0. Para este problema, Δx = L (la partícula se sabe que está en algún lugar de ese intervalo). Entonces obtenemos Δ px Δx = = (L) (0) = 0, en violación del principio de incertidumbre. ¿QUÉ ES INCORRECTO CON ESTE CÁLCULO ?




























