-
-
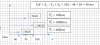
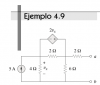
Hola Unicoos me podrian ayudar con el ejercicio xfa , me piden calcular sus voltajes y corrientes por el metodo de mallas , gracias
Raúl RC
el 10/7/17Sorry! Lamento de todo corazon no poder ayudarte, pero unicoos (por ahora) solo llega hasta bachiller con matemáticas, física y química. Tu duda se da en la "uni". Espero lo entiendas...
Aunque a veces el profe hace alguna excepción como con este vídeo que seguro que te servirá mucho, lamento no poder ayudarte más.
Francisco Javier
el 10/7/17Hola.
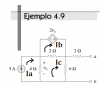
Malla b: - 2 vx + 2 (Ib - Ic) = 0
Pero: vx = 4 (Ia - Ic) → - 2 [ 4 (Ia - Ic) ] + 2 (Ib - Ic) = 0 (1)
Malla c: 2 (Ic - Ib) + 6 Ic + 4 (Ic - Ia) = 0 (2)
Ecuación Auxiliar: Ia = 5 (3)
Tenemos 3 ecuaciones con tres incógnitas. Resolviendo este sistema obtenemos:
Ia = 5 A ; Ib = 10 A ; Ic = 10/3 A
Para resistencia de 2 Ω más a la derecha: No tiene corriente ni voltaje.
Para resistencia de 6 Ω: Pasa una corriente de Ic = 10/3 A (aproximadamente 3.33 A). Y tendrá un voltaje de 6 Ic = 6 (10/3) = 20 V.
Para resistencia de 2 Ω abajo de la fuente dependiente: Pasa una corriente de Ib - Ic = 10 - (10/3) = 20/3 A (aproximadamente 6.67 A). Y tendrá un voltaje de 2 (Ib - Ic) = 2 (20/3) = 40/3 V (aproximadamente 13.33 V).
Para resistencia de 4 Ω: Pasa una corriente de Ia - Ic = 5 - (10/3) = 5/3 A (aproximadamente 1.67 A). Y tendrá un voltaje de 4 (Ia - Ic) = 4 (5/3) = 20/3 V (aproximadamente 6.67 V).
Para fuente independiente de corriente: Tiene una magnitud de 5 A. Tendrá el mismo voltaje que la resistencia de 4 Ω al estar en paralelo, osea 20/3 V (aproximadamente 6.67 V).
Para fuente dependiente de voltaje: Pasa una corriente de Ib = 10 A. Y tendrá un voltaje de 2 vx = 2 [ 4 (Ia - Ic) ] = 2{ 4 [5 - (10/3)] } = 40/3 V (aproximadamente 13.33 V).
Realizando el balance de potencia te puedes dar cuenta que lo que se consume (en resistencias) es igual a lo que se aporta (fuentes), demostrando la correcta resolución del problema.
Para dudas, házmelo saber.
-
Me ayudarian con este ejercicio?
M y m estan unidos por un hilo y el resorte esta comprimido x, cuando el hilo se corta m se dispara al circulo horizontal
Me pide el máximo valor de m para que este no deje ma pista.
Tambien (lo que no eh podido hacer) analice limite cuando M tiende a infinito.

Raúl RC
el 10/7/17Hola! Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya ha grabado como excepcion el profe. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Raúl RC
el 10/7/17Te recomiendo le eches un vistazo a los vídeos de planos inclinados con cuerdas:
https://www.youtube.com/watch?v=iq2EmDjbgHQ
https://www.youtube.com/watch?v=ufoZ1Xva2ns
A partir de ahí, se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok?
-
Buenas! Hace mucho que no paso por el foro, pero tengo una duda hace varios dìas sobre un ejercicio de termodinámica ya lo e avanzado una parte pero me falta otra:
Una mezcla de dióxido de carbono y vapor de agua contienie 0.05 kmol de vapor de agua por kmol de CO2 seco a una temperatura de 40ºC y una presión total de 100 kpa . Determine:
a)Humedad especifica(KgH2O/KgCo2 seco)
b) Humedad relativa
c) La temperatura a que se debe calentarse la mezcla par que la humedad relativa sea del 35%.
Yo e podido hallar ya el inciso a) el valor de la humedad especifica es 0.020454545 KgH2O/KgCo2seco , para esto hice un procedimiento análogo que con una mezcla de vapor de agua y aire seco.
Luego para humedad relativa yo e hallado un valor de 43.11% pero me dicen que este no es el valor correcto entonces no se como podria hallarse o en que me estoy equivocando:
-¿ Esta mezcla de vapor de agua y CO2 seco se puede tratar igual que una mezcla de vapor de agua y aire seco?
Alguna ayuda o sugerencia porfavor??
-
Profe como seria el diagrama de fuerza ( o los diagramas de fuerza), si un caballo ( el caballo pesa mas) arrastra a un carreta (La fuerza de fricción está en la ruedas). Si me ayuda se lo agradeceria mucho.
Jorge
el 8/7/17La FR (que se halla como: FR = μ · N) es siempre contraria al movimiento, es una fuerza que reduce nuestra rapidez. En el ejercicio que propones, con esos datos, no se podría conocer el sentido del movimiento, dado que el peso del caballo no nos dice nada, de hecho, aumenta aún más la FR (del propio caballo con el suelo). Lo que determinará el diagrama de fuerzas será conocer el impulso o la fuerza que ejerce el caballo para moverse, y en caso de superar ésta a la fuerza de rozamiento, quedará así:
LEYENDA y aclaraciones:
FR = Fuerza de rozamiento
μ = Coeficiente de rozamiento (Puede ser estático si el objeto está parado, o dinámico si el objeto ya se encontraba en movimiento)
N = Normal (Es una fuerza perpendicular al plano. Es aquella que evita que nos hundamos en el suelo o salgamos volando. Por ello, se cumple que el Peso es igual a la Normal (Ojo, se cumple P = N en un plano completamente horizontal, en uno inclinado correspondería a la componente Y del peso, es decir, PY = N.
T = Tensión de la cuerda que une al caballo y la carreta.
Posdata.: No uséis animales como transportes :)
-
Raúl RC
el 8/7/17Se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok?
Antonio Silvio Palmitano
el 8/7/17Observa que tienes composición entre Movimiento Vertical y Movimiento Horizontal, ambos uniformemente variados.
Establece un sistema de referencia con eje OX al nivel del suelo con sentido positivo acorde al movimiento de la pelota, eje OY vertical y positivo hacia arriba, con origen en el pie del edificio, y considera como instante inicial (t = 0) al momento de lanzamiento.
Luego, tienes los datos iniciales:
xi = 0, yi = 50 m,
vix = 0, viy = 20 m/s,
ax = 5 m/s2, ay = - g = - 9,8 m/s2.
Luego, plantea las ecuaciones de posición y de velocidad del Movimiento Rectilíneo Uniformemente Variado (te dejo la tarea) y quedan:
x = 2,5*t2
y = 50 + 20*t - 4,9*t2,
vx = 5*t
vy = 20 - 9,8*t.
a)
Plantea la condición de altura al nivel del suelo:
y = 0, sustituyes y queda:
50 + 20*t - 4,9*t2 = 0, divides en todos los términos por -1, ordenas términos y queda:
4,9*t2 - 20*t - 50 = 0, que es una ecuación polinómica cuadrática cuyas soluciones son:
t1 ≅ - 1,750 s, que no tiene sentido para este problema,
t2 ≅ 5,831 s,
luego reemplazas en las ecuaciones de posición (te dejo los cálculos) y queda:
x ≅ 85,015 m, y = 0.
Luego plantea la condición de altura máxima:
vy = 0, sustituyes y queda:
20 - 9,8*t = 0, haces pasaje de término y queda:
- 9,8*t = - 20, haces pasaje de factor como divisor y queda:
t ≅ 2,041 s,
luego reemplazas en las ecuaciones de posición (te dejo los cálculos) y queda:
x ≅ 10,412 m, y ≅ 70,408 m (observa que es aproximadamente 20,408 m por encima del nivel de la azotea).
Luego, plantea la condición de altura al nivel de la azotea:
y = 50, sustituyes y queda:
50 + 20*t - 4,9*t2 = 50, haces pasaje de término (observa que tienes cancelaciones) y queda:
20*t - 4,9*t2 = 0, ordenas términos, multiplicas en todos los términos de la ecuación por -1 y queda:
4,9*t2 - 20*t = 0, que es una ecuación polinómica cuadrática cuyas soluciones son:
t = 0, que es el instante de lanzamiento,
t ≅ 4,082 s, luego reemplazas en las ecuaciones de velocidad y queda:
vx ≅ 20,408 m/s,
vy ≅ - 20 m/s.
Luego, plantea el vector velocidad:
v = < vx , vy > ≅ < 20,408 , - 20 >, cuyo módulo queda: |v| ≅ √( 20,4082 + (- 20)2 ) ≅ √(816,486) ≅ 28,574 m/s,
luego, expresa las componentes del vector unitario que indica la dirección de la velocidad, que es tangente a la trayectoria:
u = v/|v| ≅ < 0,714 , - 0,700 >;
luego plantea la expresión del vector aceleración:
a = < ax , ay > = < 5 , - 9,8 >;
luego plantea para su componente tangencial a la trayectoria (observa que planteamos un producto escalar entre vectores):
aT = a ∗ u ≅ < 5 , - 9,8 > ∗ < 0,714 , - 0,700 > ≅ 5*0,714 - 9,8*(- 0,700) ≅ 10,430 m/s2;
luego plantea el módulo de la aceleración:
|a| = √(ax2 + ay2) ≅ √(52 + (- 9,8)2) = √(121,04) ≅ 11,002 m/s2,
luego, a partir del Teorema de Pitágoras, plantea la expresión para la componente de la aceleración que es normal a la trayectoria:
aN = √(|a|2 - aT2) ≅ √(11,0022 - 10,4302) ≅ √(12,259) ≅ 3,501 m/s2.
Espero haberte ayudado.
Antonio Silvio Palmitano
el 9/7/17c)
Observa que en el enunciado tienes las componentes horizontal (ax) y vertical (ay) de la aceleración del móvil, y observa que con estos dos datos hemos calculado el módulo de la aceleración (|a|).
Observa que hemos calculado las componentes horizontal (vx) y vertical (vy) de la velocidad, y observa que hemos calculado el módulo de la velocidad (|v|), y las componentes del vector unitario que representa la dirección de la velocidad: u = < vx/|v| , vy/|v| >.
Luego, observa que hemos planteado el producto escalar entre la aceleración y el vector unitario que expresa la dirección de la velocidad (observa que designamos θ al ángulo determinado por el vector velocidad y el vector aceleración):
a • u = desarrolla el producto escalar = |a|*|u|*cosα = |a|*|1|*cosθ = |a|*cosθ = aT.
Luego, a partir de la expresión del Teorema de Pitágoras puedes plantear para la componente normal de la aceleración:
aT2 + aN2 = a2, haces pasaje de término y queda:
aN2 = a2 - aT2, haces pasaje de potencia como raíz y queda:
aN = √(a2 - aT2),
Observa que los cálculos están hechos en el desarrollo.
Espero haberte ayudado.
Nando Hull
el 9/7/17Antonio Silvio Palmitano
el 10/7/17Se trata de una propiedad del producto escalar. En tu ejercicio, tienes el vector velocidad, que es tangente a la trayectoria, y tienes el vector aceleración.
Luego, planteamos el vector unitario u, que indica la dirección del vector velocidad, y llamamos θ al ángulo que forma este vector con el vector aceleración.
Luego, tienes las expresiones de los vectores:
a = < 5 , - 9,8 >, u = < 0,714 , - 0,700 >, y su producto escalar quedó: a • u = 10,430 m/s2.
Aquí, recuerda que hay otra forma para plantear el producto escalar entre el vector a y el vector u:
a • u = |a|*|u|*cosθ = |a|*1*cosθ = |a|*cosθ = aT.
Aquí debes tener en cuenta que la componente de un vector (a, en este ejercicio) en la dirección de un vector unitario (u, en este ejercicio) es igual al producto escalar entre el vector y el vector unitario que indica la dirección.
Espero haberte ayudado.
-
Raúl RC
el 8/7/17La opción correcta es la a) ya que ambas escalas en este caso han de ser celsius, te recomiendo que te pongas delante todas las escalas de temperaturas y sus conversiones y analices que ocurre cuando tomas P,Q,R =0, es ahi donde encontrarás qué opciones son posibles y cuales no