-
-Una partícula se mueve según la ecuación: s=4t2 +2t +3 (SI). Calcular: a) el desplazamiento en t=0; b) la velocidad inicial vo; c) la velocidad en el instante t= 2s; d) la aceleración del movimiento. Sol: s0=3m; v0 =2 m/s ; v=18 m/s ; a=8 m2/s
a) 4*0^2+2*0+3=3 m
b) y= yo +vot+1/2*9'8t^2? t es cero?
c) 4*2^2 + 2*2 +3= 23 m ; x= vt ; 23 m=v*2s ; 23/ 2= 11'5 m/s
d) como se hace? gracias de antemano
Antonio Silvio Palmitano
el 19/3/17Observa la ecuación de posición que tienes en el enunciado, en la que ordenamos términos en forma creciente y queda:
s(t) = 3 + 2t + 4t2,
luego, si la comparas con la ecuación del Movimiento Rectilíneo Uniformemente Variado:
s(t) = s0 + v0*t + (1/2)a*t2, comparas coeficientes y tienes:
s0 = 3 m (posición inicial),
v0 = 2 m/s (velocidad inicial),
(1/2)a = 4, de donde puedes despejar: a = 8 m/s2 (aceleración);
luego, puedes plantear la ecuación de velocidad para el Movimiento Rectilíneo Uniformemente Variado:
v(t) = v0 + a*t, reemplazas valores y queda:
v(t) = 2 + 8*t (si empleas derivadas, observa que la función velocidad es la derivada de la función posición).
Luego pasas a responder
a) s(0) = 3 + 2*0 + 4*02 = 3 + 0 + 0 = 3 m, que has calculado correctamente;
b) v(0) = 2 + 8*0 = 2 + 0 = 2 m/s;
c) v(2) = 2 + 8*2 = 2 + 16 = 18 m/s;
d) a = 8 m/s2 que ya hemos calculado (si empleas derivadas, observa que la función aceleración es la derivada de la función velocidad).
Espero haberte ayudado.
-
Un automóvil acelera desde el reposo a 2 m/s2 durante 20 s. La velocidad se mantiene entonces constante durante 20 s, después de los cuales experimenta una aceleración de - 3 m/s hasta que se detiene. ¿Cuál es la distancia total recorrida? la respuesta es 1466.6 m

Antonio Silvio Palmitano
el 19/3/17Planteamos el problema en tres etapas, y observa que los datos finales de una etapa son los datos iniciales de la siguiente, y observa que establecemos el origen de coordenadas en el punto de partida del móvil:
1°)
t0 = 0, t = 20 s, x0 = 0, v0 = 0, a = 2 m/s2,
luego, la posición del móvil queda:
x = x0 + v0*t + (1/2)*a*t2 = 0 + 0*t + (1/2)*2*202 = 0 + 0 + 400 = 400 m,
y la velocidad final queda:
v = v0 + a*t = 0 + 2*20 = 0 + 40 = 40 m/s.
2°)
t0 = 20 s, t = 20 + 20 = 40 s,, x0 = 400 m, v = 40 m/s (constante),
luego, la posición del móvil queda:
x = x0 + v*(t - t0) = 400 + 40*(40 - 20) = 400 + 40*20 = 400 + 800 = 1200 m.
3°)
t0 = 40 s, t = a determinar, x0 = 1200 m, v0 = 40 m/s, v = 0, a = - 3 m/s2,
luego, la posición del móvil queda:
x = x0 + v0*(t t0) + (1/2)*a*(t - t0)2, reemplazamos valores y queda:
x = 1200 + 40*(t - 40) + (1/2)*(-3)*(t - 40)2,
y la velocidad final queda:
v = v0 + a*(t - t0), reemplazamos valores y queda:
v = 40 - 3*(t - 40), distribuimos en el último término, reducimos términos numéricos y queda:
v = 160 - 3*t,
luego, como el móvil se detiene la finalizar su recorrido, planteamos:
0 = 160 - 3*t, hacemos pasaje de término y queda:
3*t = 160, hacemos pasaje de factor como divisor y queda:
t = 160/3 = 53,333 s, que es el tiempo total que emplea el móvil en realizar las tres etapas;
luego, reemplazamos en la ecuación de posición y queda:
x = 1200 + 40*(53,333 - 40) + (1/2)*(-3)*(53,333 - 40)2, resolvemos términos y queda:
x = 1200 + 533,333 - 266,667 = 1466,667 m,
que es la posición final del móvil, con respecto a su posición inicial en la primera etapa.
Luego podemos resumir:
1°) Desde x = 0 hasta x = 400 m, por lo que recorrió en esta etapa: 400 - 0 = 400 m;
2°) desde x = 400 m hasta x = 1200 m, por lo que recorrió en esta etapa: 1200 - 400 = 800 m;
3°) desde x = 1200 m hasta x = 1466,667 m, por lo que recorrió en esta etapa: 1466,667 - 1200 = 266,667 m.
Espero haberte ayudado.
-
Hola tengo una duda se puede multiplicar kwatt por segundo, o solo watt por segundo? Porque mi ejercicio dice asi:. Los motores de una fábrica tienen una potencia de 100 kwatt. Calcular que cantidad de calor (en kcal) libera al ambiente en 1hora. Yo convertí los 100 kwatt a 100000 watt, y 1h lo pasé a 3600 segundo. Entonces hice 100000 watt * 3600 segundo =. = 360000000 Joule. Y el calor sería 360000000 Joule / 4185,5 Joule/kcal = 86011,23 Kcal. Esto es así??? O en vez de convertir en watt puedo multiplicar directamente los kwatt?? Gracias. Pd: el 4185,5 es un valor fijo es el equivalente mecánico del calor. (ó 4,1855 KJoule/kcal)
Antonio Silvio Palmitano
el 19/3/17Recuerda que el prefijo "kilo" indica que debes multiplicar por mil
Tienes como datos:
Pot = 100 kW = 100 kJ/s,
Δt = 1h = 3600 s,
luego pasas al cálculo del trabajo mecánico:
W = Pot*Δt = 100 kJ/s * 3600 s = 360000 kJ,
luego, expresado en unidades de calor, queda:
Q = 360000 kJ / (4,1855 kJ/kcal) = 86011,23 kcal.
Observa que hemos supuesto que todo el trabajo se libera como calor, y observa que hemos mantenido las unidades del enunciado, y hemos llegado a tu misma respuesta.
Espero haberte ayudado.
-
Es un tema de MRUV
Si me pudieran ayudar se los agradeceri mucho
Un automovil se desplaza con una velocidad de 80km/h cuando repentinamente a una distancia de 10 metros , aparece frente a el un camion que se desplaza con una velocidad de 44km/h . Determine la desaceleracion minima que debe aplicar el automovil para no chocar con el camion
Antonio Silvio Palmitano
el 19/3/17Tienes las velocidades:
va = 80 Km/h = 80*1000m/3600s = 22,222 m/s (velocidad inicial del auto),
vc = 44 Km/h = 44*1000m/3600s = 12,222 m/s (velocidad constante del camión).
Luego planteamos las posiciones iniciales:
xa = 0,
xc = 10 m.
Luego, planteamos las ecuaciones de movimiento para cada móvil:
Xa = xa + va*t - (1/2)*a*t2
Xc = xc + vc*t,
reemplazamos valores y quedan (consideramos que el auto y el camión se desplazan en el mismo sentido):
Xa = 0 + 22,222*t - (1/2)*a*t2
(observa que el último término tiene signo negativo, con lo que a es el módulo de la desaceleración del auto),
Xc = 10 + 12,222*t,,
luego, si haces las gráficas (te dejo la tarea), verás que para el auto tenemos una rama de parábola con eje de simetría t y vértice en el origen de coordenadas, y que para el camión tenemos una recta con ordenada al origen x = 10 y pendiente m = 12,222; y observa que la rama de parábola debe encontrarse siempre "por debajo" de la recta, y por lo tanto, no debe tener puntos en común con ella.
Luego, planteamos la condición de un único punto en común (punto de tangencia) entre el tramo de parábola y el tramo de recta, y para ello planteamos:
Xc = Xa, sustituimos expresiones y queda:
10 + 12,222*t = 22,222*t - (1/2)*a*t2, hacemos pasajes de términos y queda:
(1/2)*a*t2 - 10*t + 10 = 0, multiplicamos por 2 en todos los términos de la ecuación y queda:
a*t2 - 20*t + 20 = 0, que es una ecuación polinómica cuadrática, cuyo discriminante es:
D = (-20)2 - 4*a*20 = 400 - 80*a = 80*(5 - a), y para tener solución única debe cumplirse:
D = 0, sustituimos y queda:
80*(5 - a) = 0, hacemos pasaje de factor como divisor y queda:
5 - a = 0, hacemos pasaje de término y queda:
5 = a, que es el módulo de la desaceleración (en m/s2),
reemplazamos en la ecuación y queda:
5*t2 - 20*t + 20 = 0,
cuya solución es t = 2 s (que es el tiempo que transcurre hasta que el auto alcanza al camión).
Observa que las ecuaciones de posición quedan:
Xa = 0 + 22,222*t - 2,5*t2
Xc = 10 + 12,222*t,,
observa que para t = 2 la posición de encuentro es: x = 34,444 m,
luego planteamos las ecuaciones de velocidad:
Va = 22,222 - 5*t
Vc = 12,222,
y observa que para t = 2, la velocidad de ambos móviles es: va = vc = 12,222 m/s,
por lo que tenemos que el auto alcanza al camión, pero no lo sobrepasa.
Luego concluimos que la desaceleración debe tener módulo a mayor que 5,
ya que para a = 5 tenemos que el auto tarda 2 segundos en alcanzar al camión, luego de recorrer 34,444 m, y lo hace con su misma velocidad: 12,222 m/s, por lo tanto la desaceleración debe tener, como mínimo, módulo igual a 5 m/s2.
Espero haberte ayudado.
-
Hugo
el 19/3/17Antonio Silvio Palmitano
el 19/3/17Has planteado y calculado correctamente la frecuencia de giro:
f = 700 rev / 60 s = 11,667 rev/s = 11,667 1/s = 11,667 Hz (hertzios).
Luego, para el periodo de giro planteamos:
T = 1/f = 60 s / 700 rev = 0,086 s/rev = 0,086 s (segundos).
Recuerda que "rev" (revoluciones) es una unidad de medida abstracta (y lo mismo ocurre con radianes).
Espero haberte ayudado.
-
Raúl RC
el 13/4/17TE sugiero veas previamente los videos de cinemática:
A partir de ahí, se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? -
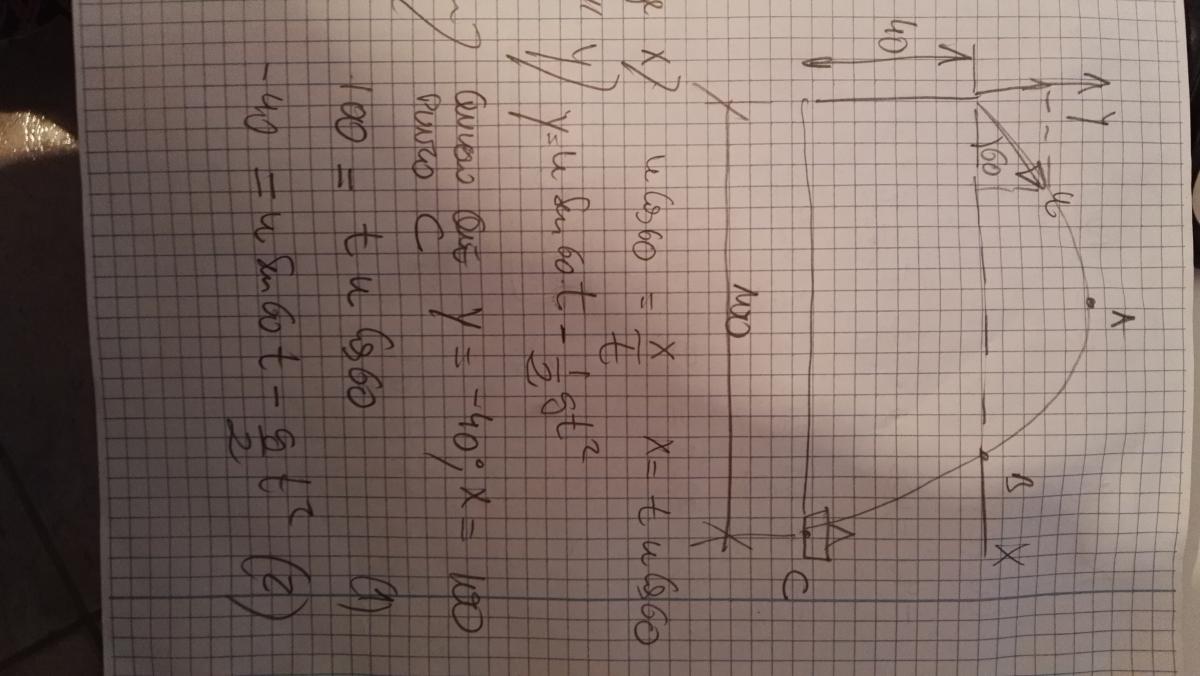
!Se lanza un proyectil con un ángulo de 60º con la horizontal desde un acantilado. El acantilado se encuentra a 40 m de altura respecto del nivel del mar. A 100 m del acantilado hay un barco Determinar: a) la velocidad inicial del proyectil para que impacte sobre el barco, b) la velocidad del proyectil en el momento del impacto, c) la máxima altura alcanzada por el proyectil. ¿Qué he hecho mal?

Paula
el 19/3/17 -
Antonio Silvio Palmitano
el 19/3/17Recuerda las ecuaciones de movimiento para un cuerpo que cae libremente desde una altura h (consideramos el sentido positivo "hacia arriba", alejándonos de la superficie del planeta):
y = h - (1/2)gt2
v = - gt,
luego, planteamos para el tiempo que tarde en llegar al suelo:
y = 0, reemplazamos en la ecuación de posición y queda:
0 = h - (1/2)gt2, hacemos pasaje de término y queda:
(1/2)gt2 = h, multiplicamos por 2/g en ambos miembros y queda:
t2 = 2h/g, hacemos pasaje de potencia como raíz y queda:
t = √(2h/g),
luego sustituimos en la ecuación de la velocidad y queda:
v = - g*√(2h/g) = - √(g2)*√(2h/g) = - √(g2*2h/g) = - √(2gh),
observa que el signo negativo indica que la velocidad tiene sentido "hacia abajo", hacia la superficie del planeta.
Luego, para una altura inicial de 1m tenemos:
v = - √(2*g*1) = - √(2g),
cuyo módulo (rapidez) queda espresado:
|v| = √(2g), en m/s,
luego, para expresar en Km/h recuerda:
m/s = 1m / 1s = (1Km/1000) / (1h/3600) = (3600/1000) km/h = 3,6 Km/h.
Por ejemplo, para el planeta Mercurio tenemos:
|v| = √(2g) = √(2*2,65) = √(5,3) = 2,302 m/s = 2,302*3,6 = 8,288 Km/h.
Espero haberte ayudado.
-
Hola me pueden recomendar livros para estudiar física clasica en la Universidad
que expliquem de uma maneira didactica que tenga ejercicios propuestos y desarrollados
gracias
-
Enunciado: Un oscilador armónico simple, ideal realiza 3 vibraciones completas en 24 segundos. Determine: el periodo del movimiento, y la frecuencia en Hertz?
1. 8s
2. 0.125s
3. 0.125Hz
4. 0.33HzSeleccione una:
a. Marque aquí, si 3 y 4 son correctas.
b. Marque aquí, si 1 y 2 son correctas.
c. Marque aquí,1 si 3 y son correctas.
d. Marque aquí, si 2 y 4 son correctas.Antonio Silvio Palmitano
el 18/3/17Recuerda que la frecuencia es el número de oscilaciones dividido el intervalo de tiempo empleado para realizarlas, por lo tanto tienes:
f = 3 osc / 24 s = (1/8) osc/s = 0,125 Hz,
y recuerda que el periodo de oscilación es igual al recíproco de la frecuencia, por lo tanto tienes:
T = 1/f = (1/0,125) s/osc = 8 s.
Espero haberte ayudado.
























 Te lo miro sin problema...
Te lo miro sin problema...





