-
Albus99
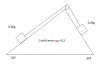
el 23/3/17Buenas tardes, tengo una duda existencial en un ejercicio de plano inclinado. Lo he resuelto tomando los dos posibles sentidos de movimiento, y en los dos casos me da una aceleración negativa, y lo he comprobado muchas veces y creo que no me he equivocado. Mi duda es que si mis cálculos son correctos, cual es la interpretación física de ese resultado puesto que los signos negativos me indican que el sentido de movimiento es el contrario al planteado, y en los dos casos me da signo negativo.
-
Mar Lobato Espejo
el 23/3/17Hola.
Que velocidad angular se ha de comunicar a una estacion espacial de forma anular de 60 metros de diametro por tal de crear una gravedad artificial a la perifera igual a la gravedad de la superficie terrestre?
Muchas gracias!
-
Kainanteh
el 23/3/17 -
Luis Alberto
el 23/3/17Algún universitario que sepa hacer este problema de choques? Un cuerpo A de masa mA=3,0kg se mueve en la dirección x positiva, con una rapidez de 10,0m/s, cuando choca contra otro cuerpo B de masa mB=6,0kg que se halla en reposo. Después del choque, A tiene una velocidad de vAd=(8,0m/s;35°) ¿Cuál es la velocidad de B después del choque?. Seleccione una:
a. (4,2 m/s; -30°)b. ( 2,2m/s;30°)c. (3,5 m/s; -63°)d. (4,7 m/s; -50°)e. (2,9 m/s; -53°)
Antonio Silvio Palmitano
el 23/3/17Observa que la cantidad de movimiento se conserva, ya que no actúan fuerzas exteriores al sistema de dos cuerpos.
Antes del choque tienes (planteamos las componentes por separado):
p1x = pA1x + pB1x = + mA*vA1 + mB*vB1 = 3*10 + 6*0 = 30 + 0 = 30 ( en Kg*m/s);
p1y = 0 (observa que el movimiento es en la dirección del eje x).
Después del choque tienes (planteamos las componentes por separado)
p2x = pA2x + pB2x = + mA*vA2*cos(35°) + mB*vB2*cos(θ) = 3*8*cos(35°) + 6*vB2*cos(θ) = 19,660 + 6*vB2*cos(θ);
p2y = pA2y + pB2y = + mA*vA2*sen(35°) + mB*vB2*sen(θ) = 3*8*sen(35°) + 6*vB2*sen(θ) = 13,766 + 6*vB2*sen(θ).
Luego, planteas las ecuaciones que resultan de igualar componente a componente:
19,660 + 6*vB2*cos(θ) = 30
13,766 + 6*vB2*sen(θ) = 0,
en las dos ecuaciones haces pasaje de término y de factor, y queda:
vB2*cos(θ) = 1,723
vB2*sen(θ) = - 2,294,
luego, divides la segunda ecuación con la primera, miembro a miembro y queda:
tan(θ) = - 1,331, luego compones con la función inversa de la tangente y tienes: θ = - 53,090°;
luego elevas al cuadrado en ambos miembros de ambas ecuaciones, sumas miembro a miembro y queda:
vB22 = (1,723)2 + (-2,294)2 = 8,231, haces pasaje de potencia como raíz y queda: vB2 = 2,869 m/s.
Luego, tienes que la rapidez del segundo cuerpo después del choque es 2,869 m/s, y que su dirección de movimiento forma un ángulo de - 53,090° con respecto al eje x, y que los cuerpos se desplazan en semiplanos distintos, con respecto al eje x.
Espero haberte ayudado.
-
Ruben
el 23/3/17 -
Usuario eliminado
el 23/3/17necesito que me ayuden con estas preguntas:
1.ejemplos de movimientos que sean aproximadamente armonicos simples. ¿por que son escasos los movimientos que sean exactamente armonicos simples?
2.que cambios se haria en un oscilador armonico para dublicar la velocidad maxima del objeto en oscilacion?
Pablo
el 23/3/171. Los claros ejemplos son los del muelle y el del péndulo. Tienen como características el oscilar entorno a un punto de equilibrio. Son escasos ya que un Movimiento Armónico Simple (MAS) de este tipo se refiere a por ejemplo, estirar un muelle, soltarlo y que se quede oscilando por un tiempo indefinidido con la misma amplitud y esto en la realidad no es posible ya que exixten las fuerzas de rozamiento que frenan el muelle y al cabo de unas cuantas oscilaciones, el muelle acabará frenándose en su posición de equilibrio. Por esto se dice que som escasos los ejemplos.
2. No entiendo muy bien la pregunta pero me puedo imaginar que se refiere a darle un estirón al muelle o al péndulo para que así aumente su velocidad. Insisto en que no entiendo muy bien lo que quiere decir el segundo apartado.
Espero haberte ayudado. Si tienes el enunciado originalno dudes en publicarlo para tratar de ayudarte
-
Daniel Ochoa
el 23/3/17Hola, por favor me podrian ayudar con esto
Antonio Silvio Palmitano
el 23/3/17Comienza por plantear las áreas de sección transversal de la tubería:
A1 = π*d12/4 = π*(3*d2)2/4 = π*9*d22/4 = 9*π*d22/4,
A2 = π*d22/4,
y observa que tienes la relación:
A1 = 9*A2 (1).
Luego, plantea la ecuación de continuidad:
A1*v1 = A2*v2, sustituyes la expresión señalada (1) y queda:
9*A2*v1 = A2*v2, haces pasaje de factores como divisores, simplificas y queda:
v1 = (1/9)*v2.
Luego, concluyes que la opción d) es la respuesta correcta.
Espero haberte ayudado.
-
torpeligente
el 22/3/17Si el voltaje total es 20V y la intensidad total es 18A, ¿la resistencia total sería igual a 1,1 periodo con la ley de Ohm en un circuito paralelo?
Más datos:
R1=5Ω; R2=5Ω; R3=2Ω
V1=20; V2=20; V3=20
I1=4A; I2=4A; I3=10A
Antonio Silvio Palmitano
el 23/3/17Si las tres resistencias están conectadas en paralelo, tienes para la resistencia total equivalente (Rp):
1/Rp = 1/R1 + 1/R2 + 1/R3, reemplazas valores y queda:
1/Rp = 1/5 + 1/5 + 1/2, resuelves el segundo miembro y queda:
1/Rp = 9/10, inviertes expresiones en ambos miembros y queda:
Rp = 10/9 = 1,111 Ω.
Luego, observa que según la expresión de la Ley de Ohm tenemos:
V/Rp = (20) / (10/9) = 18 A.
Espero haberte ayudado.
-
Luis
el 22/3/17¡Buenas! Necesito ayuda para este problema:
Un cilindro de 5 cm de altura y 2 cm de radio pesa 1,7N en el aire y 1N cuando lo sumergimos completamente. Calcula la fuerza de empuje y la densidad del líquido.
¡Gracias de antemano!
Pablo
el 22/3/17La fuerza de empuje es 1,7N - 1N = 0,7 N ya que ese deducimos que ese 0,7 es la fuerza que hace el líquido sobre el cilindro a lo que se le llame empuje. Por lo tanto el empuje = 0,7 N.
Para hallar la densidad del líquido hay que saber la fórmula: E = v · d · g
E = Empuje (0,7N)
v = volumen del cuerpo sumergido (en este caso el del cilindro)
d = densidad del líquido (lo que nos están preguntando)
g = gravedad (9,8 o 10 m/s2 según el profesor)
Pablo
el 22/3/17Se me ha olvidado comentarte que el volumen del cilindro es π · h · r2 siendo h la altura (0,05m) y r el radio de la base (0,02m).
Te recuerdo que hay que pasar las unidades a sistema internacional (SI) por eso te he puesto las dimensiones del cilindro en metros.
Espero haberte ayudado
