-
Hola unicoos, me falta este ejercicio para completar una guía de ejercicios. Es dinámica circular con conservación de la energía, creo, la verdad no se como plantear un problema combinado así. El problema es el siguiente.
Un péndulo está formado por una masa m atada una cuerda ideal de longitud L=1,5m. La máxima apertura angular que el péndulo tiene en su movimiento es de 30° (medida respecto a la vertical). ¿Cuál es la máxima rapidez que el péndulo puede alcanzar?.
a. 2,0 m/s b. 2,2 m/s c. 3,1 m/s d. 2,5 m/s e. 2,7 m/s
Raúl RC
el 13/4/17Te sugiero este video..
https://www.youtube.com/watch?v=Tk5GlL1s_6Q
A partir de ahí, se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? -
Me podrían ayudar con este problema?

Hice esto, pero no sé si es correcto
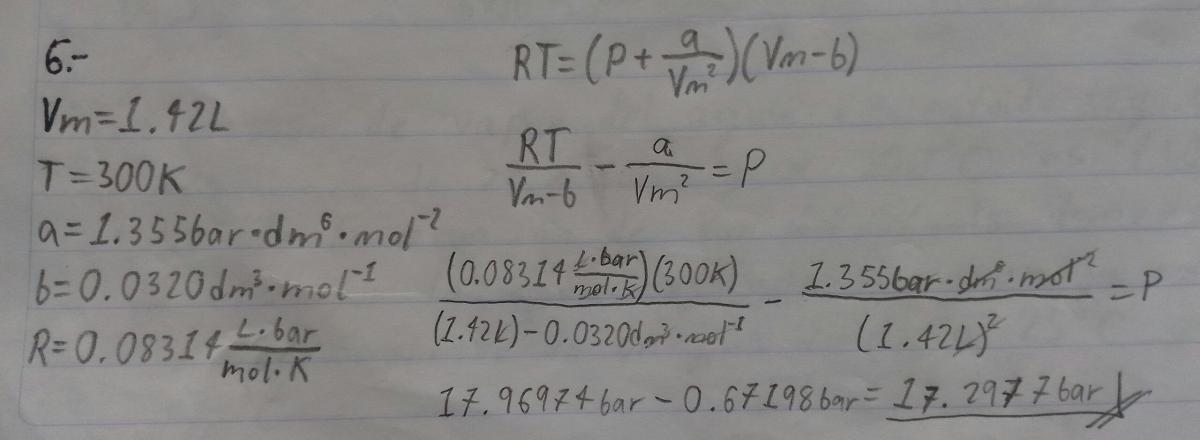
-
Hola, buenas tardes:
¿Me podrían decir en qué se han basado y por qué para resolver este problema? Muchas gracias.
-
Necesito ayuda con esta pregunta
por lo que se.. que la respuesta es el literal c. pero me podrian explicar ir diciendo por que los demas literales no pueden ser la respuesta correcta :/
Francisco Javier
el 12/3/17Se descartan las opciones a) y b) por el principio de la conservación de masa. El flujo másico para una tubería con una entrada y una salida es igual independiente de la sección transversal y la velocidad. La opción d) tampoco puede ser ya que si el fluido fuera incompresible (densidad constante), el flujo másico permanece constante y en el enunciado vemos que no es así. La única manera de explicar que el flujo masico de entrada sea distinto al de salida, es que en la tubería haya un cambio de densidad, ósea un flujo compresible.
-
Se deja caer una pelota desde 80 m de altura. Un segundo más tarde, una pelota es lanzada desde el suelo verticalmente con una velocidad de 40 m/s.
Determina a qué altura desde el suelo se encuentran
¿Alguien que me ayude por favor? Gracias
Francisco Javier
el 12/3/17Ecuación de posición para la pelota situada en la altura: y = yo + vot - 0.5gt2 = 80 - 4.905t2 (1)
Ecuación de posición para la pelota situada en el suelo: y = yo + vot - 0.5gt2 = 40(t - 1) - 4.905(t - 1)2 (2)
Se encuentran cuando sus posiciones son iguales. Igualo las ecuaciones antes planteadas para hallar el tiempo de encuentro:
80 - 4.905t2 = 40(t - 1) - 4.905(t - 1)2 → t ≈ 2.51 s
El choque se produce 2.51 s despues que se suelta la pelota que está en la altura.
Para saber la altura a la que ocurre el choque reemplazamos el tiempo en (1) o en (2): y = 80 - 4.905*2.512 ≈ 49.1 m
Para dudas, házmelo saber.
-
- Se deja caer un cuerpo de 2kg por un plano inclinado 30° respecto de la horizontal y sin rozamiento. El cuerpo recorre 20m en este plano inclinado y a continuación se mueve en un plano horizontal que tiene un coeficiente de rozamiento de 0,25 hasta pararse. Calcula:
a) La energía mecánica del cuerpo.
b) La velocidad del cuerpo después de haber recorrido los 20m en el plano inclinado.
c) La distancia recorrida en el plano horizontal hasta pararse.
¿Podéis ayudarme, por favor? Con las respuestas me bastaría pero si me decís cómo es el procedimiento me haríais un gran favor.
Antonio Silvio Palmitano
el 12/3/17Observa que la altura del plano inclinado, que corresponde al punto de inicio del movimiento del cuerpo es:
h = 20*sen30° = 10 (en m).
Luego, tratamos el problema en dos partes (observa que consideramos que la altura es cero en el plano horizontal):
1) desplazamiento del cuerpo por el plano inclinado (desde el punto inicial A hasta el punto B en el pie del plano inclinado),
2) desplazamiento del cuerpo por el plano horizontal (desde el punto B hasta el punto final C).
1)
En el punto A tenemos: hA = 10, vA = 0, luego su energía mecánica inicial es:
EMA = EPA + ECA = MghA + (1/2)MvA2 = 20*9,8*10 + (1/2)*20*02= 1960 (en J).
En el punto B tenemos: hB = 0, vB = a determinar, luego su energía mecánica en el pie del plano es:
EMB = EPB + ECB = MghB + (1/2)MvB2 = 20*9,8*0 + (1/2)*20*vB2 = 10vB2 (en J).
Luego, como el plano inclinado es liso y no ejerce rozamiento, y como no actúan fuerzas externas que aporten trabajos, tenemos que la energía se conserva, por lo que planteamos:
EMB = EMA, sustituimos y queda:
10vB2 = 1960, hacemos pasaje de factor como divisor y queda:
vB2 = 196, hacemos pasaje de potencia como raíz y queda:
vB = 14 (en m/s).
2)
Observa que el módulo de la fuerza de rozamiento es: fr = μN = μMg = 0,25*20*9,8 = 49 (en N),
y observa que la dirección de la fuerza de rozamiento es opuesta a la dirección de movimiento del cuerpo, por lo que el trabajo de la fuerza de rozamiento queda:
Wfr = - fr*s = - 49s (en J);
observa también que la energía mecánica en el punto B es: EMB = 1960 (en J),
y que la energía mecánica en el punto C es igual a cero, por lo que planteamos:
Wfr = EMC - EMB, sustituimos y queda:
- 49*s = 0 - 1960, resolvemos el segundo miembro, hacemos pasaje de factor como divisor y queda:
s = 40 (en m).
Te dejo para que hagas los gráficos, con los diagramas de fuerzas, y observa que hemos empleado el Sistema Internacional de Unidades de Medida MKS.
Espero haberte ayudado.
-
¿podrias ayudarme? con esta problema de física
Se lanza un cuerpo verticalmente hacia arriba con una velocidad inicial de 90 km/h despreciando la resistencia del aire
a)¿Qué altura alcanzará?
b)¿cuánto tiempo tardara en llegar de nuevo al punto de partida?
Gracias
Antonio Silvio Palmitano
el 12/3/17Tienes el módulo de la velocidad inicial:
v0 = 90 (en Km/h) = 90*1000/3600 = 25 (en m/s).
Luego, recuerda las ecuaciones del Tiro Vertical (consideramos que la altura inicial es igual a cero):
y = v0*t - (1/2)*g*t2
v = v0 - g*t,
reemplazamos valores y queda (consideramos: g = 9,8 m/s):
y = 25t - 4,9*t2
v = 25 - 9,8*t.
Luego, pasamos a la resolución del problema:
a)
Recuerda que en el punto cumbre de la trayectoria, la altura es máxima y la velocidad es nula, por lo que planteamos:
v = 0, sustituimos y queda:
25 - 9,8*t = 0, hacemos pasaje de término y queda:
- 9,8*t = - 25, hacemos pasaje de factor como divisor y queda:
t ≅ 2,551 (en s), que es el tiempo que tarda el cuerpo en alcanzar el punto cumbre,
luego reemplazamos en la ecuación de posición y la altura máxima queda:
yM ≅ 25*2,551 - 4,9*2,5512 ≅ 31,888 (en m).
b)
Observa que al punto inicial de la trayectoria le corresponde altura igual a cero, por lo que planteamos:
y = 0, sustituimos y queda:
25t - 4,9*t2 = 0, extraemos factor común y queda:
t*(25 - 4,9*t) = 0, luego por anulación de un producto tenemos dos opciones:
a)
t = 0, que es el instante inicial,
b)
25 - 4,9*t = 0, hacemos pasaje de término y queda:
- 4,9*t = - 25, hacemos pasaje de factor como divisor y queda:
t ≅ 5,102 (en s), que es el tiempo que transcurre hasta que el cuerpo alcanza nuevamente su punto de partida.
Espero haberte ayudado.
-
Como se resuelve esto?
Dos cosechadoras autopropulsadas M y M´ parten simultaneamente de la localidad A hacia la localidad B y en ese mismo instante parte otra M´´ de la localidad B hacia la localidad A.
L distancia A-B es de 90km y las velocidades de los moviles son de 6km/h, 5 km/h y 9 km/h respectivamente.Determinar grafica y analiticamente los tiempos en que:
a)M equidista de M´ y M´´
b)M´ equidista de M y M´´
c)M´´ equidista de M y M´
d)Ocurren los encuentros.
Antonio Silvio Palmitano
el 12/3/17Consideramos las posiciones: x = 0 (localidad A) y x = 90 (localidad B).
Luego, las ecuaciones de movimiento rectilíneo uniforme para los tres móviles quedan:
x = 0 + 6t (cosechadora M),
x' = 0 + 5t (cosechadora M '),
x'' = 90 - 9t (cosechadora M'').
a) M se encuentra en medio, con M' a su izquierda y M'' a su derecha
x'' - x = x - x', sustituimos y queda:
90 - 9t - 6t = 6t - 5t, hacemos pasajes de términos y queda:
- 16t = - 90, hacemos pasaje de factor como divisor y queda:
t = 5,625 (en h),
observa que las posiciones de los móviles son: x = 33,75, x' = 28,125, x'' = 39,375 (todas en Km).
b) M' se encuentra en medio (observa que es el móvil más lento), con M'' a su izquierda y M a su derecha:
x' - x'' = x - x', sustituimos y queda:
5t - (90 - 9t) = 6t - 5t, distribuimos en el primer miembro, resolvemos el segundo miembro y queda:
5t - 90 + 9t = t, hacemos pasajes de términos y queda:
13t = 90, hacemos pasaje de factor como divisor y queda:
t ≅ 6,923 (en h),
observa que las posiciones de los móviles son: x = 41,538, x' = 34,615, x'' = 27,693 (todas en Km).
c)M'' se encuentra en medio, con M a su derecha y M' a su izquierda:
x - x'' = x'' - x', sustituimos y queda:
6t - (90 - 9t) = 90 - 9t - 5t, distribuimos en el primer miembro, reducimos términos semejantes en el segundo y queda:
6t - 90 + 9t = 90 - 14t, hacemos pasajes de términos y queda:
29t = 180, hacemos pasaje de factor como divisor y queda:
t ≅ 6,207 (en h),
observa que las posiciones de los móviles son: x = 37,242, x' = 31,035, x'' = 34,137 (todas en Km).
d)
Observa que las cosechadoras M y M' parten juntas, por lo que sus coordenadas de encuentro son: t = 0, x = 0.
Para las cosechadoras M y M'' planteamos:
x = x'', sustituimos y queda:
6t = 90 - 9t, hacemos pasaje de término y queda:
15t = 90, hacemos pasaje de factor como divisor y queda:
t = 6 (en h), para lo que corresponde la posición: x = 36 (en Km).
Para las cosechadoras M' y M'' planteamos:
x' = x'', sustituimos y queda:
5t = 90 - 9t, hacemos pasaje de término y queda:
14t = 90, hacemos pasaje de factor como divisor y queda:
t ≅ 6,429 (en h), para lo que corresponde la posición: x ≅ 32,143 (en Km).
Queda para que hagas los gráficos cartesianos tiempo-posición.
Espero haberte ayudado.
-
Hola.. me podrian explicar como se calcula el trabajo en fluidos? tengo ese ejercicio y no se como calcular el trabajo
cuanto trabajo efectua la presion al bombear 1.6
 de agua por un tubo de 15 mm de diametro interno si la direccion de presion entre los extremos del tubo es de 1.2 atm?
de agua por un tubo de 15 mm de diametro interno si la direccion de presion entre los extremos del tubo es de 1.2 atm?David
el 7/4/17Raúl RC
el 13/4/17Si aplicamos una fuerza “F” sobre una sección transversal “A” del conducto y le produce un desplazamiento “X”, el trabajo “W” de la fuerza “F” será
[1]……………………W = F * X
En ese desplazamiento longitudinal “X” se ha desplazado un volumen “V” de fluido que será
[2]…………………..V = A * X …………..de aquí que…………X = V / A
Remplazando en [1]
[3]……………………..W = F * V / A
En esta fórmula se ve que (F/A = presión hidrostática P en la sección)
[4]…………………….W = P * V
Si consideramos ahora dos secciones que identificamos con A₁ y A₂ en dos puntos (1) y (2) del conducto y además consideramos que el líquido avanza de (1) hacia (2) porque las presiones son
[5]………………………...P₁ > P₂
Entonces el trabajo neto “W” será
[6]…………………………W = W₁ - W₂ = (P₁ - P₂) * V = Δ P * V
Para el caso del problema
Δ P = 1.2 atm = 121 600 Pa
V = 1.6 m³
[7]…………………………W = ΔP * V = 121 600 Pa * 1.6 m³ = 170 240 J
Del desarrollo del teorema de Trabajo-Energía, que es aplicable a este caso de un fluido, se deduce el teorema de Bernoullie que es en el que se basa este ejercicio -
Como se resuelve esto?
Una hormiga que se desplaza con MRU pasa en T1=5s ,por X1=5 m y en T2=10s por X2=30m ,en base a estos datos determinar:
a)Ecuacion horaria del movimiento
b)Posicion cuando t=0
C)En que instante paso por el origen de coordenadas.
d) Graficar x/t y v/t
Antonio Silvio Palmitano
el 12/3/17Primero planteamos la velocidad:
v = (x2 - x1)/(t2 - t1) = (30 - 5)/(10 - 5) = 25/5 = 5 (en m/s).
a)
Planteamos la ecuación de movimiento:
x - x1 = v*(t - t1), reemplazamos y queda:
x - 5 = 5*(t - 5), distribuimos y queda:
x - 5 = 5t - 25, hacemos pasaje de término y queda:
x = 5t - 20 (en m).
b)
Reemplazamos t = 0 y queda:
x = 5*0 - 20 = 0 - 20 = - 20 (en m).
c)
Reemplazamos x = 0 y quda:
0 = 5t - 20, hacemos pasaje de término y queda:
- 5t = - 20, hacemos pasaje de factor como divisor y queda:
t = 4 (en s).
Queda para que hagas los gráficos tiempo-posición (es un tramo recto inclinado),
y tiempo-velocidad (es un tramo recto paralelo al eje t).
Espero haberte ayudado.





























