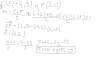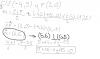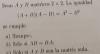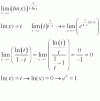-
¿Podrían decirme si lo hice bien y no tuve errores? Este tema no se me da muy bien. El enunciado es el siguiente.
Halla la ecuación de la mediatriz del segmento cuyos extremos se indican a continuación:
-
-
Me pide que clasifique el sistema en función de los distintos resultados que a el parametro "a". No se si he sacado bien los resultados de "a", ya que no se cuantas ecuaciones hay que escoger y para hayar los rangos sin determinantes habría que sustituir en la ultima matriz no?
Tengo mañana el exámen de selectividad!!
Antonio Silvio Palmitano
el 5/6/18Te muestro otra forma.
Observa que tienes un sistema de tres ecuaciones lineales y de primer grado, con tres incógnitas, por lo que planteas su determinante, y queda:
D =
1 1 -1
a 2 -1
2 a -1;
luego, desarrollas el determinante (lo hacemos según su primera fila), y queda
D = (-2+a) - (-a+2) - (a2-4), distribuyes agrupamientos, reduces términos semejantes, y queda:
D = -a2 + 2a.
Luego, tienes dos opciones:
1°)
D ≠ 0, sustituyes la expresión del determinante, y queda:
-a2 + 2a ≠ 0, multiplicas en todos los términos de la ecuación por -1, y queda:
a2 - 2a ≠ 0, que es una ecuación polinómica cuadrática negada, en la que tienes:
a ≠ 0 y a ≠ 2, por lo que tienes que el sistema es compatible determinado (con solución única) si a pertenece al conjunto: R - { 0 , 2 }.
2")
a)
a = 0,
reemplazas en el sistema, y su matriz ampliada queda:
1 1 -1 0
0 2 -1 0
2 0 -1 0;
a la tercera fila le restas el doble de la primera, y queda:
1 1 -1 0
0 2 -1 0
0 -2 1 0;
a la tercera fila se sumas la segunda fila, y queda:
1 1 -1 0
0 2 -1 0
0 0 0 0;
a la primera fila le restas la segunda fila multiplicada por 1/2, y queda:
1 0 -1/2 0
0 2 -1 0
0 0 0 0;
y puedes observar que la submatriz cuyos elementos hemos remarcado es de orden 2 con su determinante distinto de cero, por lo que el sistema es compatible indeterminado (con infinitas soluciones), y su expresión es:
x - (1/2)z = 0, aquí sumas (1/2)z en ambos miembros, y queda: x = (1/2)z,
2y - z = 0, aquí sumas z y luego multiplicas por 1/2 en ambos miembros, y queda y = (1/2)z;
luego, las soluciones del sistema quedan expresadas:
x = (1/2)z,
y = (1/2)z,
z ∈ R;
b)
a = 2,
reemplazas en el sistema, y su matriz ampliada queda:
1 1 -1 2
2 2 -1 6
2 2 -1 6;
a la tercera fila le restas la segunda fila, y queda:
1 1 -1 2
2 2 -1 6
0 0 0 0;
a la segunda fila le restas el doble de la primera, y queda:
1 1 -1 2
0 0 1 2
0 0 0 0;
a la primera fila le sumas la segunda, y queda:
1 1 0 4
0 0 1 2
0 0 0 0;
y puedes observar que la submatriz cuyos elementos hemos remarcado es de orden 2 con su determinante distinto de cero, por lo que el sistema es compatible indeterminado (con infinitas soluciones), y su expresión es:
x + y = 4, aquí restas y en ambos miembros, y queda: x = -y + 4,
z = 2;
luego, las soluciones del sistema quedan expresadas:
x = -y + 4,
y ∈ R,
z = 2.
Espero haberte ayudado.
-
El ejercicio dos no se plantear la ecuación de la condición ni si la ecuacion de la función es el área.
Y en el tres no se plantear las probabilidades, habria que hacerlo con una tabla como la probabilidad condicionada?
-
Llevo un rato intentado acabar esta integral indefinida pero me he quedado atascado,
¿que podría hacer ahora?
Adjunto foto de lo que he hecho hasta ahora
¡Muchas gracias!
Antonio Silvio Palmitano
el 5/6/18Tienes la integral:
I = ∫ x1/2*(lnx)2*dx;
luego, has planteado bien el Método de Integración por Partes:
u = (lnx)2, de donde tienes: du = 2*lnx*(1/x)*dx,
dv = x1/2*dx, de donde tienes: v = (2/3)*x3/2 (omitimos la constante arbitraria en este paso);
luego, aplicas el método, y queda:
I = (lnx)2*(2/3)*x3/2 - ∫ (2/3)*x3/2*2*lnx*(1/x)*dx;
aquí ordenas factores en el primer término, extraes y resuelves factores constantes en la integral, reduces potencias con bases iguales, y queda:
I = (2/3)*x3/2*(lnx)2 - (4/3)*∫ lnx*x1/2*dx;
luego, planteas el Método de Integración por Partes, y tienes:
U = lnx, de donde tienes: dU = (1/x)*dx,
dV = x1/2*dx, de donde tienes: V = (2/3)*x3/2 (omitimos la constante arbitraria en este paso);
luego, aplicas el método, y queda:
I = (lnx)2*(2/3)*x3/2 - (4/3)*[ lnx*(2/3)*x3/2 - ∫ (2/3)*x3/2*(1/x)*dx ];
luego, distribuyes el segundo término, ordenas factores, extraes y reduces factores en la integral, y queda:
I = (2/3)*(lnx)2*x3/2 - (8/9)*x3/2*lnx + (8/9)*∫ x1/2*dx;
luego, resuelves la última integral, y queda:
I = (2/3)*(lnx)2*x3/2 - (8/9)*x3/2*lnx - (16/27)*x3/2 + C.
Luego, puedes derivar para verificar la validez de la solución general cuya expresión hemos remarcado:
I ' = (4/3)*lnx*x1/2 + (lnx)2*x1/2 - (4/3)*x1/2*lnx - (8/9)*x1/2 + (8/9)*x1/2;
luego cancelas términos opuestos, y observa que tienes el argumento de la integral de tu enunciado.
Espero haberte ayudado.
-
Hola.
¿Cuál sería el límite cuando x tiende a infinito de: (lnx)1/(1-lnx)?
Me gustaría saber cómo es desarrollado, sin sustituir por números altos para ver a qué tiende, ya que sustituyendo por números altos lo tengo hecho y me da 1, sin embargo desarrollando con logaritmos a ambos lados me da 1/e.
Gracias.
Saludos.