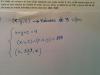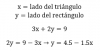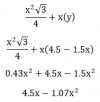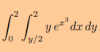-
Roger Pilacuán
el 18/5/18 -
Carlos José Guillén Colón
el 18/5/18Buenas noches Unicos, de verdad necesito que por favor me ayuden con esta integral, en la guía me piden hacerla por sustitución simple (cambio de variables), en casi de que no salga por así, no importa, si por favor me ayudan, se los agradecería mucho.
-
Alfredo Pérez
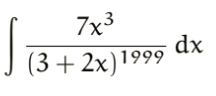
el 18/5/18Hola, me podrían ayudar con el siguiente ejercicio por favor. Gracias de antemano.
Sea R la región triangular del plano xy limitado por x=0, y=0, x+y=1, encontrar el valor de R e^(x-y/x+y)
-
fabian
el 18/5/18Hola necesito ayuda con este ejercicio
El hexagono A es rotado en 180° con respecto al origen , obteniendose el hexagono B como muestra la figura
¿Cual es el lado correspondiente a P en el hexagono B?
¿Seria r? Tengo un poco oxidado esros conocimientos
-
fabian
el 18/5/18Hola tengo dudas con este ejercicio
En un juego compuesto por 4 muñecas matrioskas la altura de cada una de ellas corresponde a 2/3 de la muñeca anterior Si la más pequeña mide 8 cm Que altura tiene la muñeca más grande?A) 17cm , B) 24 cm , C) 27 cm , D) 64 cm
La única solución que se me ocurre es
8 ÷ (2/ 3)= 12( segunda muñeca)
12÷ (2/3) = 18 (tercera muñeca)
18÷ (2/3) = 27 (cuarta muñeca)
Esta correcto?. Si lo esta no entiendo porque debo dividir por 2/3.
Antonio Silvio Palmitano
el 18/5/18Has planteado y resuelto el problema en forma clara y correcta.
Observa que para ir "de mayor a menor" debes multiplicar por 2/3, por lo que has planteado que para ir "de menor a mayor" debes dividir por 2/3.
Vamos "de mayor a menor":
27*(2/3) = 18,
18*(2/3) =12,
12*(2/3) = 8.
Y tu has hecho ya el recorrido "de menor a mayor".
Espero haberte ayudado.
-
lbp_14
el 18/5/18Hola Unicoos
No tengo ni idea de cómo se hace.
Me lo podéis resolver PASO A PASO porfavor?
MUCHAS GRACIAS
Sebastian Quintero
el 18/5/18
Antonio Silvio Palmitano
el 18/5/18Vamos con una orientación.
Has denominado: x a la cifra de las centenas, y a la cifra de las decenas, z a la cifra de las unidades, por lo que el número queda desarrollado:
100x + 10y + z.
La primera ecuación está correcta:
x + y + z = 9 (1).
Para la segunda ecuación debes plantear:
(100x + 10y + z) - (100z + 10y + x) = 198, eliminas los agrupamientos, y queda:
100x + 10y + z - 100z - 10y - x = 198, reduces términos semejantes (observa que tienes cancelaciones, y queda:
99x - 99z = 198, divides por 99 en todos los términos de la ecuación, y queda:
x - z = 2 (2).
Para la tercera ecuación debes plantear:
(x + z)/2 = y, multiplicas por 2 en ambos miembros, y queda:
x + z = 2y, resta 2y en ambos miembros, y queda:
x - 2y + z = 0 (3).
Luego, solo queda que resuelvas el sistema que tienes con las ecuaciones señaladas (1) (2) (3).
Haz el intento de terminar la tarea, y si te resulta necesario no dudes en volver a consultar.
Espero haberte ayudado.
-
Alejaa Winkii
el 18/5/18 -
Bryan
el 18/5/18 -
Alfredo Pérez
el 17/5/18Me pueden echar una mano con el siguiente ejercicio por favor, se los agradecería muchísimo.
6) El recinto R del plano xy lo acotan; y =x², x =y², y² =2x, y =2x². El cambio de variables x² =uy, y² =vx lleva el recinto R en un rectángulo del plano uv. Si se anota por T` a esta transformación. ¿Cuál es su jacobiano?
-
Samuel Cabaleiro Villar
el 17/5/18¿Puedes hacer un vídeo de las gráfica lineales y no lineales que tengo examen y no me sale?
Sebastian Quintero
el 17/5/18
