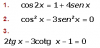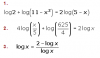-
Buenas tardes Unicoos!
Me han mandado un ejercicio que no se resolver, a ver si podeis echarme una mano:
Mil gracias!
Antonio Silvio Palmitano
el 7/5/18Tienes la expresión de la función (observa que factorizamos su denominador):
f(x) = (b*x-1)/(x-2)2, cuyo dominio es: D = R - {2}.
Luego, planteas la expresión de la función derivada, y queda:
f ' (x) = ( b*(x-2)2 - (b*x-1)*2*(x-2) )/(x-2)4;
luego, planteas la condición de valor crítica para x = -1 como indica tu enunciado:
f ' (-1) = 0, sustituyes la expresión de la función derivada evaluada en el primer miembro, y queda:
( b*(-3)2 - (-b-1)*2*(-3) )/(-3)4 = 0, multiplicas en ambos miembros por (-3)4, y queda:
b*(-3)2 - (-b-1)*2*(-3) = 0, resuelves coeficientes, distribuyes el segundo término, y queda:
9*b - 6*b - 6 = 0, reduces términos semejantes, sumas 6 en ambos miembros, y queda:
3*b = 6, divides por 3 en ambos miembros, y queda:
b = 2.
Luego, sustituyes el valor remarcado en la expresión de la función, y queda:
f(x) = (2*x-1)/(x-2)2;
y sustituyes también en la expresión de la función derivada, y queda:
f ' (x) = ( 2*(x-2)2 - (2*x-1)*2*(x-2) )/(x-2)4,
extraes factor común en el numerador, reduces expresiones, y queda:
f ' (x) = 2*(x-2)*(-x-1)/(x-2)4,
simplificas, extraes factor común -1 en el numerador, y queda:
f ' (x) = -2*(x+1)/(x-2)3.
Luego, puedes plantear la condición de valor crítico, y queda:
f ' (x) = 0, sustituyes la expresión de la función derivada en el primer miembro, y queda:
-2*(x+1)/(x-2)3 = 0, multiplicas en ambos miembros por (x-2)3, y por -1/2, y queda:
x + 1 = 0, restas 1 en ambos miembros, y queda:
x = -1, que es el único valor crítico que presenta la función.
Luego, evalúas la expresión de la función para este valor, y también para uno que sea menor que él (por ejemplo x = -2), y para otro que sea menor que él (por ejemplo x = 0), y queda:
f(-2) = (2*(-2)-1)/(-2-2)2 = -5/16 = -0,3125,
f(-1) = (2*(-1)-1)/(-1-2)2 = -3/9 = -1/3 ≅ -0,3333,
f(0) = (2*(0)-1)/(0-2)2 = -1/4 = -0,2500,
por lo que tienes que la gráfica de la función presenta mínimo en x = -1.
Espero haberte ayudado.
-
Antonius Benedictus
el 7/5/18Una vez visto que las rectas no coinciden ni son paralelas, pueden pasar dos cosas:
Que sean coplanarias (y, por tanto, se corten). Esto sucede cuando los vectores directores y el vector que une un punto de una de ellas con otro punto de la otra no determinan volumen ninguno. por lo que su producto mixto vale 0.Que no lo sean (o sea, que se crucen). En este caso, dicho producto mixto (o determinante) es distinto de 0.
-
Holaa, me podeis ayudar con este problema por favor ?? Gracias !!
En un colegio hay 60 alumnos de Bachillerato. De ellos 40 estudian inglés, 24 estudian francés y los 12 los dos idiomas. Se elige un alumno al azar:
a) Calcule la probabilidad de que estudie al menos un idioma. Sol: 0,867
b)Calcule la probabilidad de que estudie francés sabiendo que también estudia ingles. Sol: 0,3
c)Calcule la probabilidad de que no estudie inglés. Sol: 0,333
-
hola! por favor alguien me ayuda con este problema y recomendarme que videos me sirven para practicarlo?
La variación, en céntimos de euro, de la cotización bursátil de las acciones de una empresa sigue la función V(t) = t 3 − 12t 2 + 45t, en la sesión del día entre las 09:00 y las 17:00 horas (0 ≤ 𝑡 ≤ 8).
a) ¿Cuál ha sido la variación al cerrar la sesión? ¿Cuál ha sido la cotización final sabiendo que ayer cotizaba a 30€?
b) Hallar los intervalos horarios en que la variación ha crecido y aquellos en que ha decrecido, así como los extremos relativos, y la variación en esos momentos
Antonio Silvio Palmitano
el 7/5/18a)
Evalúas la expresión de la función variación (cuyo dominio es el intervalo cerrado [0,8]) para el cierre de las operaciones de bolsa del día de hoy, y queda:
V(8) = (8)3 - 12(8)2 + 45(8) = 512 - 768 + 360 = 104 céntimos = 1,04 euros;
luego, puedes plantear para la cotización de la acciones al cierre de las operaciones en el día de hoy:
p = 30 + 1,04 = 31,04 euros.
b)
Planteas la expresión de la función derivada de la variación, y queda:
V ' (t) = 3t2 - 24t + 45;
luego, planteas la condición de valor crítico (posible máximo o posible mínimo de la función), y queda:
3t2 - 24t + 45 = 0, divides por 3 en todos los términos de la ecuación, y queda:
t2 - 8t + 15 = 0,
que es una ecuación polinómica cuadrática, cuyas soluciones son: t1 = 3 y t2 = 5;
luego, tienes que estos valores críticos y los extremos del dominio dividen a éste en intervalos, para los que elegimos un valor testigo y evaluamos la función derivada, a fin de determinar el crecimiento o decrecimiento de la función:
(0,3), representado por: t = 1, y para él tienes: V ' (1) = 3 - 24 + 45 = 24 > 0, por lo que la función crece en este intervalo;
(3,5), representado por: t = 4, y para él tienes: V ' (4) = 64 - 32 + 15 = 47 > 0, por lo que la función crece en este intervalo;
(5,8), representado por: t = 6, y para él tienes: V ' (6) = 36 - 48 + 15 = 3 > 0, por lo que la función crece en este intervalo;
luego, evalúas la expresión de la función para los extremos del dominio y para los valores críticos, y queda:
V(0) = 0 - 0 + 0 = 0, por lo que la variación al comienzo de las operaciones es igual a cero,
V(3) = 27 - 108 + 135 = 54, por lo que la variación en este instante es 0,54 euros,
V(5) = 125 - 300 + 225 = 50, por lo que la variación en este instante es 0,50 euros,
V(8) = 512 - 768 + 360 = 104, por lo que la variación en este instante es 1,04 euros.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 7/5/18Recuerda las identidades trigonométricas:
cos(2x) = cos2x - sen2x (1),
cos2x = 1 - sen2x (2),
tanx = senx/cosx (3),
cotgx = 1/tanx (4).
Observa que expresamos las soluciones en radianes (1 radián = 180°).
1)
Tienes la ecuación trigonométrica:
cos(2x) = 1 + 4senx, aplicas la identidad señalada (1), y queda:
cos2x - sen2x = 1 + 4senx, aplicas la identidad señalada (2), y queda:
1 - sen2x - sen2x = 1 + 4senx, restas 1 y restas 4senx en ambos miembros, reduces términos semejantes, y queda:
2sen2x - 4senx = 0, divides por 2 en todos los términos, extraes factor común, y queda:
senx(1 - 2senx) = 0, y por anulación de un producto tienes dos opciones:
a)
senx = 0, compones en ambos miembros con la función inversa del seno, y queda:
x = kπ, con k ∈ Z;
b)
1 -2senx = 0, restas 1 en ambos miembros, divides por 2 en todos los términos, y queda:
senx = 1/2, compones en ambos miembros con la función inversa del seno, y quedan dos opciones:
b1)
x = π/6 +2mπ, con m ∈ Z (en el primer cuadrante);
b2)
x = 5π/6 +2nπ, con n ∈ Z (en el segundo cuadrante).
2)
Tienes la ecuación trigonométrica:
cos2x - 3sen2x = 0, restas cos2x en ambos miembros, y queda:
-3sen2x = -cos2x, divides por -3 en todos los términos, y queda:
sen2x = (1/3)cos2x, divides por cos2x en ambos miembros, y queda:
sen2x/cos2x = 1/3, aplicas la identidad señalada (3), y queda:
tan2x = 1/3, extraes raíz cuadrada en ambos miembros, y quedan dos opciones:
a)
tanx = √(1/3), compones en ambos miembros con la función inversa de la tangente, y queda:
x = π/6 + 2kπ, con k ∈ Z (en el primero y en el tercer cuadrante);
b)
tanx = -√(1/3), compones en ambos miembros con la función inversa de la tangente, y queda:
x = 5π/6 + 2mπ, con m ∈ Z (en el segundo y en el cuarto cuadrante).
3)
Tienes la ecuación trigonométrica:
2tanx - 3cotgx - 1 = 0, aplicas la identidad señalada (4), y queda:
2tanx - 3/tanx - 1 = 0, multiplicas en todos los términos por tanx, y queda:
2tan2x - 3 - tanx = 0, ordenas términos, y queda:
2tan2x - tanx - 3 = 0,
que es una ecuación polinómica cuadrática si consideras a tanx como su incógnita, cuyas soluciones son:
a)
tanx = -1, compones en ambos miembros con la función inversa de la tangente, y queda:
x = (3/4)π + kπ, con k ∈ Z (en el segundo y en el cuarto cuadrante);
b)
tanx = 3/2, compones en ambos miembros con la función inversa de la tangente, y queda (en forma aproximada):
x ≅ 0,313π + mπ, con m ∈ Z (en el primero y en el tercer cuadrante).
Espero haberte ayudado.
-
Hola buenas, hoy en el examen de la uni nos han puesto este ejercicio y no he sabido resolverlo. Sabemos que una función es una continua si existen dos números a, b tales que:
f (x) = cos x; si x és negativo.
f (x) = a + x2 ; si x esta entre 0 y 1.
f (x) = b / x; si x es más grande que 1.
Calcula los valores de a y de b, si sabemos que f (x) es derivable en 0 y 1, haga un boceto del gráfico de la función.
Muchas gracias.
Antonio Silvio Palmitano
el 7/5/18Tienes la expresión de la función definida a trozos, cuyo dominio es R:
f(x) =
cosx si x < 0,
a determinar si x = 0,
a + x2 si 0 < x < 1,
a determinar si x = 1,
b/x si x > 1.
Luego, planteas la definición de continuidad para los dos puntos de corte x1 = 0 y x2 = 1 por separado:
1°)
Para x1 = 0:
a)
f(0) = a determinar,
b)
Lim(x→0-) f(x) = Lim(x→0-) cosx = 1,
Lim(x→0+) f(x) = Lim(x→0+) (a + x2) = a,
luego, para que el límite exista debe cumplirse la igualdad de los límites laterales, y tienes:
a = 1,
c))
defines el valor de la función para el punto de corte para que la función sea continua, y tienes:
f(0) = 1;
2°)
Para x2 = 1:
a)
f(1) = a determinar,
b)
Lim(x→1-) f(x) = Lim(x→1-) (a + x2) = a + 1 = 1 + 1 = 2,
Lim(x→1+) f(x) = Lim(x→0+) (b/x) = b,
luego, para que el límite exista debe cumplirse la igualdad de los límites laterales, y tienes:
b = 2,
c))
defines el valor de la función para el punto de corte para que la función sea continua, y tienes:
f(1) = 2;
luego, reemplazas los valores remarcados en la expresión de la función, y queda:
f(x) =
cosx si x < 0,
1 si x = 0,
1 + x2 si 0 < x < 1,
2 si x = 1,
2/x si x > 1.
y observa que la función es continua en todo su dominio;
luego, planteas la expresión de su función derivada, y queda:
f ' (x) =
-senx si x < 0,
0 si x = 0,
2x si 0 < x < 1,
no está definida si x = 1,
-2/x2 si x > 1;
y observa que la función es derivable en el primer punto de corte (para x1 = 0 tienes un indicio porque los límites laterales de la expresión de la función derivada son iguales a 0),
pero observa que la función derivada no está definida en el segundo punto de corte (para x2 = 1 tienes que el límite lateral por izquierda es igual a 2 y tienes que el límite lateral por derecha es igual a 1), por lo que es conveniente que consultes con tus docentes por la derivabilidad de la función en este punto.
Espero haberte ayudado.
-
Como resuelvo el siguiente problema? Calcula el área limitada por la parábola y = x2 - 3x + 2, al eje de abscisas i a las rectes x = 0 i a x = 4. Gracias
Antonio Silvio Palmitano
el 7/5/18Haz un gráfico, y observa que te quedan determinadas tres regiones:
a)
cuya forma es parecida a un triángulo, limitada superiormente por un tramo de parábola, inferiormente por un tramo del eje OX, y lateralmente por izquierda por un tramo del eje OY, y observa que sus vértices son los puntos: (0,0), (1,0) y (0,2); y para su área puedes plantear:
Aa = 0∫1 ( (x2-3x+2) - (0) )*dx = [ x3/3-3x2/2+2x ] = evalúas = 1/3 - 3/2 + 2 = 5/6;
b)
que está limitada superiormente por un tramo del eje OX en inferiormente por un tramo de la parábola, y observa que sus vértices son los puntos: (1,0) y (2,0); y para su área puedes plantear:
Ab = 1∫2 ( (0) - (x2-3x+2) )*dx = [ -x3/3+3x2/2-2x ] = evalúas = -2/3 - (-5/6) = -2/3 + 5/6 = 1/6;
c)
cuya forma es parecida a un triángulo, limitada superiormente por un tramo de parábola, inferiormente por un tramo del eje OX, y lateralmente por derecha por un tramo de la recta cuya ecuación es x = 4, y observa que sus vértices son los puntos: (2,0), (4,0) y (4,6); y para su área puedes plantear:
Ac = 2∫4 ( (x2-3x+2) - (0) )*dx = [ x3/3-3x2/2+2x ] = evalúas = 16/3 - 2/3 = 14/3;
luego, planteas que el área total es igual a la suma de las áreas de las tres regiones, y queda:
A = Aa + Ab + Ac = 5/6 + 1/6 + 14/3 =17/3.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 7/5/18Vamos con una ayuda.
Tienes la sustitución (cambio de variable):
t = x + 1/x (1);
luego, elevas al cuadrado en ambos miembros de la expresión señalada (1), y tienes:
t2 = (x + 1/x)2, desarrollas el segundo miembro, y queda:
t2 = x2 + 1 + 1/x2, restas 1 en ambos miembros, y queda:
t2 - 1 = x2 + 1/x2 (2);
luego, elevas al cubo en ambos miembros de la expresión señalada (1), y tienes:
t3 = (x + 1/x)3, desarrollas el segundo miembro, y queda:
t3 = x3 + 3x + 3/x + 1/x3, extraes factor común entre los dos términos centrales del segundo miembro, y queda:
t3 = x3 +3(x + 1/x) + 1/x3, sustituyes la expresión señalada (1) en el término central del segundo miembro, y queda:
t3 = x3 + 3t + 1/x3, restas 3t en ambos miembros, y queda:
t3 - 3t = x3 + 1/x3 (3).
Luego, solo queda que sustituyas las expresiones señaladas (1) (2) (3) en la expresión de la función que tienes en tu enunciado, y podrás continuar y terminar la tarea sin problemas.
Espero haberte ayudado.