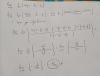-
lbp_14
el 6/5/18Hola Unicoos
Me ayudan con el apartado d)
MUCHAS GRACIAS
Antonio Silvio Palmitano
el 7/5/18Tienes una variable aleatoria con distribución binomial (X: "cantidad de individuos de la muestra que opinan favorablemente, que puede tomar los valores: 0, 1, 2, 3, 4, 5), cuyos parámetros son: n = 5 y p = 0,45, cuya probabilidad complementaria es: q = 1 - p = 0,55.
a)
P(X = 2) = C(5,2)*0,452*0,553.
b)
p(X > 2) = 1 - p(X ≤ 2) = 1 - p(X = 0) - p(X = 1) - p(X = 2) =
= 1 - C(5,0)*0,450*0,555 - C(5,1)*0,451*0,554 - C(5,2)*0,452*0,553.
c)
Observa que la esperanza de la variable aleatoria (pero ahora con los parámetros n = 1000 y p = 0,45, con la probabilidad complementaria q = 0,55) queda expresada:
E(X) = n*p = 1000*0,45 = 450 personas,
por lo que puedes concluir que la cantidad de personas esperada que tendrán opinión desfavorable es:
550 personas.
Espero haberte ayudado.
-
Olga Solana
el 6/5/18
Perdonen, no sé la mecánica para realizar las preguntas. Tengo pendiente una respuesta a este problema:
Les envío una tabla de datos y necesito saber cómo se calcula el Nivel de confianza (95,0%):
tabla de datos:
184
8
11
12
13
12
16
17
18
18
25
32
34
36
38
48
64
66
71
84
87
137
138
143
168
178
386
424
767
842
861
874gracias.
Antonius Benedictus
el 8/5/18¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
123
el 6/5/18El propietario de un inmueble tiene alquilados los cuarenta pisos del mismo a 500 € al mes cada uno, pero piensa que podría sacar mayores beneficios si aumentara el precio del alquiler. Decide intentarlo, pero observa que, por cada 50€ de aumento en el
precio del alquiler, pierde un inquilino, que se traslada a un piso más económico. ¿Cuál es el precio del alquiler que más beneficios reporta al propietario?
Antonio
el 6/5/18la función que relaciona número de veces que aumenta el alquiler con beneficios sería b(n)=(40-n)·(500+50n)
el dominio sería 0, 1, 2, 3,...., 39, 40
con n=0 se quedaría como hasta ahora y con n=40 se quedaría sin inquilinos
optimizando dicha función, es decir, derivando e igualando a cero:
b'(n)=-(500+50n)+50(40-n)=-500-50n+2000-50n=1500-100n
1500-100n=0 => n=15
comprobemos que, efectivamente, es un máximo:
b'(n)=1500-100n => b''(n)=-100=> b''(15)=-100<0 => Máx
por lo que con n=15 aumentos conseguiría el máximo de beneficios
como solución, tendríamos que hacer 15 aumentos de 50 euros perdiendo 15 inquilinos, es decir, cobrar 1250 € por piso
-
123
el 6/5/18El propietario de un inmueble tiene alquilados los cuarenta pisos del mismo a 500 € al mes cada uno, pero piensa que podría sacar mayores beneficios si aumentara el precio del alquiler. Decide intentarlo, pero observa que, por cada 50€ de aumento en el
precio del alquiler, pierde un inquilino, que se traslada a un piso más económico. ¿Cuál es el precio del alquiler que más beneficios reporta al propietario?
-
123
el 6/5/18COMO SE RESUELVAN? NO PUEDO HACERLA.
El propietario de un inmueble tiene alquilados los cuarenta pisos del mismo a 500 € al mes cada uno, pero piensa que podría sacar mayores beneficios si aumentara el precio del alquiler. Decide intentarlo, pero observa que, por cada 50€ de aumento en el precio del alquiler, pierde un inquilino, que se traslada a un piso más económico. ¿Cuál es el precio del alquiler que más beneficios reporta al propietario?
-
Marta
el 6/5/18 -
Ashley
el 6/5/18Hoola unicoos me podeis ayudar con este problema ?? Gracias !!
A partir de 5 matemáticos y 7 físicos hay que construir una comisión formada por 4 miembros elegidos al azar.
a) Calcule la probabilidad de que todos los miembros sean matemáticos. (Sol: 0,0101)
b) Calcule la probabilidad de que la comisión está formada por 2 físicos y 2 matemáticos. (Sol: 0,424)
c) calcule la probabilidad de que no haya ningún matemático. (Sol: 0,0707)
-
lbp_14
el 6/5/18 -
lbp_14
el 6/5/18
Hola Unicoos1) No sé como escribir la probabilidad de que tenga al menos un defecto y la probabilidad de que un coche no sea defectuoso.
He puesto P(D) Y P(D') porque no sé como se expresa.
2) Me dicen si las probabilidades halladas son correctas?
MUCHAS GRACIAS
-
Sergio
el 6/5/18Hola.
¿Cuál estaría bien resuelto y en qué falla el que no lo está?
Gracias.
Un saludo.
