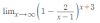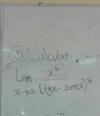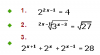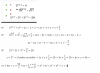-
lbp_14
el 6/5/18
Hola UnicoosMe dicen si lo he hecho bien??
MUCHAS GRACIAS
-
lbp_14
el 6/5/18Hola Unicoos
No sé como hacerlo, me podrian ayudar?
MUCHAS GRACIAS
Un juego consiste en lanzar dos dados. Si la diferencia entre los puntos de ambos es impar, ganamos. En cambio, si la diferencia es par, perdemos.
Calcula la probabilidad de ganar y la de perder.
Rasyer
el 6/5/18Hola,
Mostremos todas las probabilidades de ganar:
Diferencia 0: (1,1) ; (2,2) ; (3,3) ; (4,4) ; (5,5) ; (6,6)
Diferencia 2: (3,1) ; (1,3) ; (2,4) ; (4,2) ; (3,5) ; (5,3) ; (4,6) ; (6,4)
Diferencia 4: (6,2) ; (2,6) ; (5,1) ; (1,5)
Son 18 casos favorables en total, son 36 los casos posibles, Pr(ganar) = 18/36 = 1/2 -
Lsslie
el 6/5/18 -
Santiago951
el 6/5/18 -
Joao
el 6/5/18 -
lbp_14
el 6/5/18
Hola UnicoosMe ayudan con los tres últimos apartados?
MUCHAS GRACIAS
Rasyer
el 6/5/18Hola,
Primero hay que tener claras las leyes de Morgan, por ejemplo A ∪ B = A ∩ B, y A ∩ B = A ∪ B
Dicho esto:
b) A ∩ B = A ∪ B = {2,5,6} ∪ {1,3,4,5} = {1,3,4,5} ∪ {2,5,6} = {1,2,3,4,5,6}
c) A ∪ B = {2,5,6} ∪ {1,3,4,5} = {1,3,4,5} ∪ {2,5,6} = {1,2,3,4,5,6}
d) A ∪ (B ∩ C) = {2,5,6} ∪ ({1,3,4,5} ∩ {4,5,6}) = {2,5,6} ∪ {4,5} = {2,4,5,6}
-
Berthin Alexander
el 6/5/18 -
Jules
el 6/5/18Hola Unicoos, a ver si alguien me ayuda con este problema que no sé cómo plantear...
Un futbolista chuta un balón que está en el suelo describiendo el balón una trayectoria que viene dada por la ecuación h= - 0,01x^2 + 0,4x, siendo la x la distancia en horizontal en metros desde el punto origen de lanzamiento y h es la altura a la que se encuentra el balón en función de x. Si a 30 metros del punto de lanzamiento hay un muro de 2,5 metros de altura:
1. determina si el balón pasará por encima del muro, chocará contra este o caerá antes de llegar al muro.
2. calcula la altura máxima, hm, que alcanzará el balón y a qué distancia en horizontal (xm) del punto de lanzamiento se alcanzará dicha altura máxima.
muchas gracias!
-
lbp_14
el 6/5/18Hola Unicoos
1) Todas estas fórmulas son correctas o hay alguna que está mal??
2) Si teneis algun formulario de todas las formulitas de probabilidad pasádmela por favor.
MUCHAS GACIAS
Antonio Silvio Palmitano
el 7/5/18Debes corregir la última línea:
p[(A∩C)∩Cc] = aplicas la definición de probabilidad del suceso complementario, y queda:
= 1 - p[ ( (A∩C)∩Cc )c ] = aplicas la Ley de De Morgan ( (X∩Y)c = Xc∪Yc ), y queda:
= 1 - p[ (A∩C)c∪C ] = aplicas la Ley de De Morgan ( (X∩Y)c = Xc∪Yc ), y queda:
= 1 - p[ Ac∪Cc∪C ].
Espero haberte ayudado.
-
Rubén
el 6/5/18
