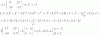Tienes la expresión de la función vectorial de posición de los puntos de la trayectoria, y obesrva que sus componentes son:

x = cost,

y = sent,

z = 3,

y observa que la ecuación remarcada corresponde a un plano paralelo al plano OXY, que pasa por el punto cuya expresión es: C(0,0,3), por lo que tienes que la trayectoria está incluida en este plano;

luego, elevas al cuadrado en ambos miembros de las dos primeras ecuaciones, y queda:

x² = cos²t,

y² = sen²t;

luego, sumas miembro a miembro, aplicas la identidad trigonométrica fundamental en el primer miembro, y queda la ecuación:

x² + y² = 1,

que corresponde a un cilindro circular con eje OZ y radio R = 1;

por lo que puedes concluir que los puntos de la trayectoria son los puntos de una circunferencia que es la curva intersección entre el plano y el cilindro cuyas ecuaciones hemos remarcado, y observa que la circunferencia tiene centro: C(0,0,3), y radio: R = 1.

Luego, plantea la expresión de la función vectorial derivada:

X ' (t) = -sent*i + cost*j + 0*k;

luego, planteas el producto escalar entre las expresiones de la función vectorial de posición y de su función derivada, y queda:

X(t) • X ' (t) =

sustituyes las expresiones vectoriales, y queda:

= ( cost*i + sent*j + 3*k ) • ( -sent*i + cost*j + 0*k ) =

desarrollas el producto escalar, y queda:

= cost*(-sent) + sent*cost + 3*0 =

resuelves el primer término y el último término, y queda:

= -cost*sent + sent*cost + 0 =

cancelas términos opuestos, y queda:

= 0,

por lo que puedes concluir que X(t) y X ' (t) son perpendiculares para todo valor del parámetro t.

Espero haberte ayudado.

Recuerda la expresión del volumen de un prisma recto (V_P) en función de la superficie de su base (S_B), y de su altura (h):

S_B*h = V_P, reemplazas el valor del volumen que tienes en tu enunciado, y queda:

S_B*h = 300, divides por h en ambos miembros de la ecuación, y queda:

S_B = 300/h (1).

Recuerda la expresión del volumen de una pirámide recta (V_R) en función de la superficie de su base (S_B), y de su altura (h), que coinciden con la superficie de la base y de la altura del prisma, respectivamente:

V_R = (1/3)*S_B*h.

Luego sustituyes la expresión señalada () en el primer miembro, y queda:

V_R = (1/3)*(300/h)*h, simplificas, y queda:

V_R = 100 cm³.

Espero haberte ayudado.

a)

Puedes llamar x₀ = 270 euros al precio inicial (día 0).

Luego, observa que el precio en cada día va a ser igual al 90 % del precio del día anterior

Luego, tienes para el precio del día 1: x₁ = x₀*0,90.

Luego, tienes para el precio del día 2: x₂ = x₁*0,90 = x₀*0,90².

Luego, tienes para el precio del día 3: x₃ = x₂*0,90 = x₀*0,90³.

Luego, puedes inferir para el precio del día n:

x_n = x₀*0,90ⁿ, con n ∈ N, n ≥ 0.

luego, reemplazas el valor del precio inicial, y queda:

x_n = 270*0,90ⁿ, con n ∈ N, n ≥ 0.

Luego, puedes plantear la inecuación:

x_n ≤ 150, sustituyes la expresión remarcada en el primer miembro, y queda:

270*0,90ⁿ ≤ 150, 

divides por 270 en ambos miembros (observa que no cambia la desigualdad), y queda:

0,90ⁿ ≤ 5/9,

tomas logaritmos decimales en ambos miembros (recuerda que la función logaritmos decimal es estrictamente creciente, por lo que no cambia la desigualdad) y queda:

log(0,90ⁿ) ≤ log(5/9), 

aplicas la propiedad del logaritmo d una potencia en el primer miembro, y queda:

n*log(0,90) ≤ log(5/9),

reemplazas los valores numéricos (observa que los puedes aproximar con tu calculadora), y queda:

n*(-0,0458) ≤ -0,2553,

divides en ambos miembros por -0,0458 (observa que si cambia la desigualdad), y queda:

n ≥ 5,5788,

por lo que puedes concluir que la compra debe ser realizada en el sexto día, o en algún otro día posterior, para que el precio a pagar no supere 150 euros.

Espero haberte ayudado.

b)

Puedes llamar x al precio a pagar, y a partir de tu enunciado, tienes la ecuación:

x_n ≤ (1/2)*x₀,

sustituyes la expresión del precio en el día genérico n que tienes en el desarrollo anterior, y queda:

x₀*0,90ⁿ ≤ (1/2)*x₀,

divides en ambos miembros por x₀ (observa que no cambia la desigualdad), y queda:

0,90ⁿ ≤ 1/2,

tomas logaritmos decimales en ambos miembros, aplicas la propiedad del logaritmo de una potencia en el primer miembro, y queda:

n*log(0,90) ≤ log(1/2),

reemplazas los valores numéricos aproximados, y queda:

n*(-0,0458) ≤ -0,3010,

divides por -0,0458 en ambos miembros (observa que si cambia la desigualdad), y queda:

n ≥ 6,5788,

por lo que tienes que a partir del séptimo día puedes realizar la compra.

Espero haberte ayudado.

Polinomios

Busca en vídeos, Matemáticas, 1º Bachillerato, y ahí lo tienes todo.

1

Para que sean coincidentes, todos los puntos de r deben estar también en s, y al contrario también. En la solución, pone un punto que pertenece a r, pero no a s, y por tanto es imposible que sean coincidientes.

Saludos.

Entonces lo que deberia hacer sería coger el P(0,0,0) de la recta r y sustituirlo en x, y, z de la recta s de tal manera que si no dan igual las 3 incógnitas no son coincidentes ?? Gracias !!

Tienes que coger el (0,0,0) por ejemplo y sustituirlo en las dos ecuaciones de s, y como ves que la segunda no la cumple, pues has terminado.

Saludos.

LO veo claro preo a ver si asi lo ves mejor