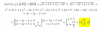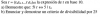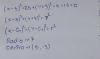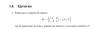-
Buenas,
intento hacer este ejercicio pero me da todo el rato resultado negativo -4 y - 5 cuando debería darme lo mismo en positivo y no sé qué puedo estar haciendo mal.
Este es el enunciado:
La edad actual de un entrenador es un número de dos cifras con las siguientes características.
1. la suma de las dos cifras es igual a una sexta parte de su edad
2. hace 9 años, la edad de éste tenía los mismos dígitos que la actual pero intercambiados.
¿qué edad tiene el entrenador?
Muchas gracias!!
Antonio Silvio Palmitano
el 22/4/18Puedes llamar x a la cifra de las decenas, y puedes llamar y a la cifra de las unidades.
La edad actual del entrenador queda expresada: 10x + y.
La edad del entrenador hace nueve años queda expresada: 10x + y - 9.
1)
1x + y = (1/6)*(10x + y), multiplicas por 6 en todos los términos de la ecuación, y queda:
6x + 6y = 10x + y, restas 6x y resta y en ambos miembros, y queda:
5y = 4x (1).
2)
10x + y - 9 = 10y + x, restas x, restas y y sumas 9 en ambos miembros, y queda:
9x = 9y + 9, divides por 9 en todos los términos de la ecuación, y queda:
x = y + 1 (2).
Luego, sustituyes la expresión señalada (1) en la ecuación señalada (2), y queda:
5y = 4*(y + 1), distribuyes el segundo miembro, y queda:
5y = 4y + 4, restas y en ambos miembros, y queda:
y = 4;
luego, reemplazas el valor remarcado en la ecuación señalada (2), resuelves, y queda:
x = 5;
luego, reemplazas los valores remarcados en la expresión de la edad del entrenador, que también tienes remarcada,
resuelves, y tienes que la edad del entrenador es: 54 años.
Espero haberte ayudado.
-
Los puntos A(-1, 3) y B(3, -3), son vértices de un triángulo isósceles ABC que tiene su vértice C en la recta 2x − 4y + 3 = 0 siendo AC y BC los lados iguales. Calcular las coordenadas del vértice C.
Antonio Silvio Palmitano
el 22/4/18Puedes expresar al vértice que debes determinar: C(x,y).
Luego, planteas la expresión de la longitud del lado AC, y queda:
|AC| = √( (x+1)2 + (y-3)2 ).
Luego, planteas la expresión de la longitud del lado BC, y queda:
|AC| = √( (x-3)2 + (y+3)2 ).
Luego, plantea la relación entre las longitudes de ambos lados:
|AC| = |AB|, sustituyes expresiones, y queda:
√( (x+1)2 + (y-3)2 ) = √( (x-3)2 + (y+3)2 ), elevas al cuadrado en ambos miembros, y queda:
(x+1)2 + (y-3)2 = (x-3)2 + (y+3)2;
desarrollas los binomios elevados al cuadrado en ambos miembros, y queda:
x2 + 2x + 1 + y2 - 6y + 9 = x2 - 6x + 9 + y2 + 6y + 9,
restas x2 y restas y2 en ambos miembros, reduces términos semejantes, y queda:
2x - 6y + 10 = -6x + 6y + 18, divides por 2 en todos los términos de la ecuación, y queda:
x - 3y + 5 = -3x + 3y + 9, sumas 3x, restas 3y y restas 5 en ambos miembros, y queda:
4x - 6y = 4, divides por 2 en todos los términos de la ecuación, y queda:
2x - 3y = 2 (1).
Luego, como el vértice C pertenece a la recta, tienes que sus coordenadas verifican la ecuación que tienes en el enunciado:
2x - 4y + 3 = 0, sumas 4y y restas 3 en ambos miembros, y queda:
2x = 4y - 3, divides por 2 en todos los términos de la ecuación, y queda.
x = 2y - 3/2 (2).
Luego, sustituyes la expresión señalada (2) en la ecuación señalada (1), y queda:
2(2y - 3/2) - 3y = 2, distribuyes el primer término, reduces términos semejantes, y queda:
y - 3 = 2, sumas 3 en ambos miembros, y queda: y = 5;
luego, reemplazas el valor remarcado en la ecuación señalada (2),resuelves, y queda: x = 17/2;
y puedes concluir que el tercer vértice de triángulo isósceles queda expresado: C( 17/2 , 5 ).
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 22/4/18Vamos con una orientación.
Tienes al número natural r expresado en base 10, luego, puedes plantear su desarrollo con múltiplos de potencias de 10:
r = rn*10n + rn-1*10n-1 + ... + r2*102 + r1*10 + r0;
a1)
Extraes factor común 10 entre todos los términos menos el último, y queda:
r =10*(rn*10n-1 + rn-1*10n-2 + ... + r2*10 + r1) + r0;
luego, tienes que el primer término es múltiplo de 10 y, por lo tanto también es divisible por 5,
por lo que debe cumplirse que el último término también debe ser divisible por 5.
a2)
Tienes que 5 divide a r0, por lo tanto existe un número natural n tal que: r0 = 5*n (1);
luego, extraes factor común 10 entre todos los términos menos el último, y queda:
r =10*(rn*10n-1 + rn-1*10n-2 + ... + r2*10 + r1) + r0;
luego, expresas a 10 como producto de factores primos, sustituyes la expresión señalada (1) en el último término, y queda:
r = 5*2*(rn*10n-1 + rn-1*10n-2 + ... + r2*10 + r1) + 5*n,
extraes factor común 5 entre los dos términos de la expresión, y queda:
r =5*( 2*(rn*10n-1 + rn-1*10n-2 + ... + r2*10 + r1) + n),
por lo que tienes que r es múltiplo de 5, por lo que tienes también que 5 divide a r.
b)
Asocias todos los términos del desarrollo excepto los dos últimos, y queda:
r = (rn*10n + rn-1*10n-1 + ... + r3*103 + r2*102) + r1*10 + r0;
extraes factor común 100 en el primer término, asocias los dos últimos términos, y queda:
r = 100*(rn*10n-2 + rn-1*10n-1 + ... + r3*10 + r2) + (r1*10 + r0);
luego, observa que el primer término es múltiplo de 100 = 25*4, por lo tanto tienes que el primer término es divisible por 25,
por lo que debe cumplirse que el último término: (r1*10 + r0) debe ser divisible por 25.
Luego, observa que el criterio de divisibilidad por 25 puede expresarse:
"un número natural r es divisible por 25, si el número natural formado por sus últimas dos cifras también lo es".
Espero haberte ayudado.
-
Hola, ¿Cómo doy 5 puntos del plano que estén a distancia 2 del punto A= (3,1)?
Luis Cano
el 22/4/18La circunferencia es el lugar geométrico cuyos puntos están a igual distancia del centro. Entonces basta obtener la ecuación de la circunferencia con centro en (3,1) y radio 2 que esta dada por: (x-3)²+(y-1)²=2². Ahora solo dale valores a "x" para obtener los de "y". Cualquier duda comenta :)