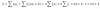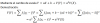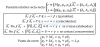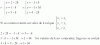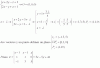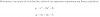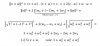-
Hola, una pregunta, en el apartado a) que calculos hay que hacer para saber que las rectas no son coincidentes ?? Gracias !
Antonio Silvio Palmitano
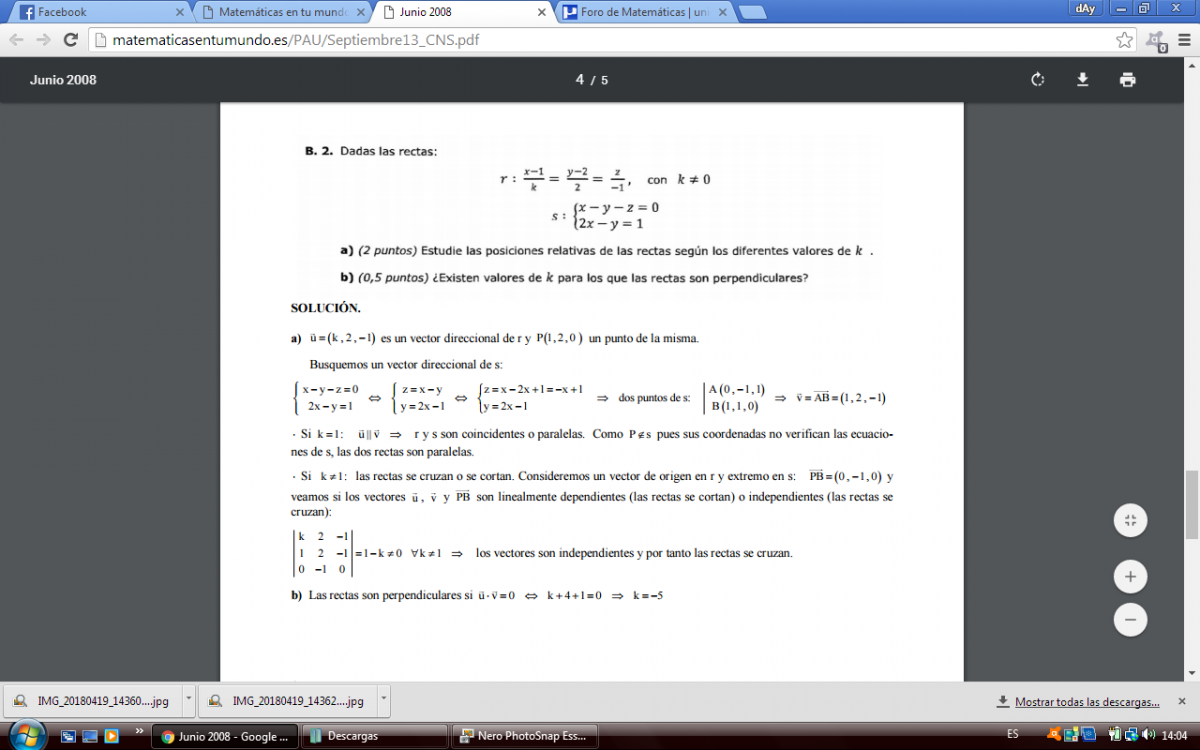
el 21/4/18Observa que tienes las ecuaciones cartesianas simétricas (o continuas) de la recta r,
y tienes que el punto A(1,2,0) pertenece a la recta r, cuyo vector director queda expresado: ur = <k,2,-1>.
Luego, observa que si reemplazas las coordenadas del punto A en las ecuaciones de la segunda recta, quedan las igualdades:
-1 = 0,
0 = 1,
que son absurdas, por lo que tienes que el punto A no pertenece a la segunda recta, por lo que puedes concluir que la recta r y la recta s no son coincidentes para cualquier valor k.
Luego, observa que tienes a la recta s presentada como intersección entre dos planos, por lo que puedes plantear que su vector director es el producto vectorial entre los vectores normales a los planos, y tienes:
us = <1,-1,-1> x <2,-1,0> = <-1,-2,1>.
a)
1)
Planteas la condición de paralelismo (los vectores directores son paralelos, por lo que el producto vectorial entre ellos es nulo):
urx us = O, sustituyes expresiones, y queda:
<k,2,-1> x <-1,-2,1> = <0,0,0>, resuelves el producto vectorial, y queda:
<0,1-k,-2k+2> = <0,0,0>;
luego, por igualdad entre vectores, igualas componente a componente, y queda el sistema:
0 = 0 (observa que es una identidad verdadera),
1 - k = 0, aquí sumas k en ambos miembros, y queda: 1 = k,
-2k + 2 =0, aquí divides por 2 en todos los términos, y queda: -k +1 = 0, sumas k en ambos miembros, y queda: 1 = k;
luego, puedes concluir que las rectas son paralelas para k = 1.
2)
Plantea la condición de perpendicularidad entre los vectores directores (por lo que tienes que el producto escalar entre ellos es igual a cero):
ur • us = 0, sustituyes expresiones, y queda:
<k,2,-1> • <-1,-2,1> = <0,0,0>, resuelves el producto escalar, y queda:
-k - 4 - 1 = 0, sumas k en ambos miembros, reduces términos semejantes, y queda: -5 = k,
por lo que tienes que las rectas pueden ser perpendiculares o alabeadas para k = -5.
Luego, reemplazas el valor remarcado en las ecuaciones simétricas de la recta r, igualas a un parámetro (t) a cada uno de sus miembros, y queda el sistema de ecuaciones:
(x - 1)/5 = t, de aquí despejas: x = 1 + 5t (1),
(y - 2)/2 = t, de aquí despejas: y = 2 + 2t (2),
z/(-1) = t, de aquí despejas: z = -t (3);
luego, a fin de investigar si existe un punto de intersección entre las dos rectas,sustituyes las expresiones señaladas (1) (2) (3) en las ecuaciones cartesianas implícitas de la recta s, y queda:
(1+5t) - (2+2t) - (-t) = 0, resuelves el primer miembro, y queda: 4t - 1 = 0, de aquí despejas: t = 1/4,
2(1+5t) - (2+2t) = 1, resuelves el primer miembro, y queda: 8t =1, de aquí despejas: t = 1/8,
y como tienes que los valores del parámetro no coinciden tienes que las rectas no se cortan, y resultan ser alebeadas con vectores directores perpendiculares entre sí, pero tienes que las rectas no son perpendiculares para cualquier valor k, porque no tienen punto de intersección.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 21/4/18Recuerda la expresión de la longitud de una circunferencia en función de su radio:
L = 2π*R (1).
Recuerda la expresión de la longitud de una cuerda en función de la medida del ángulo que subtiende:
Lc = 2*R*sen(θ/2) (2).
7)
Reemplazas el dato de tu enunciado en la ecuación señalada (1), y queda:
14π = 2π*R, divides en ambos miembros por 2π y queda:
7 cm = R;
luego, reemplazas el valor remarcado y la medida del ángulo que tienes en tu enunciado en la ecuación señalada (2), y queda:
Lc = 2*7*sen(80°/2) = 14*sen(40°) cm,y solo queda que hagas el cálculo.
8)
Reemplazas los datos de tu enunciado en la ecuación señalada (2), y queda:
2 = 2*5*sen(θ/2), divides por 10 en ambos miembros de la ecuación, y queda:
0,2 = sen(θ/2), compones con la función inversa del seno (observa que debes emplear tu calculadora), y queda:
11,537° ≅ θ/2, multiplicas por 2 en ambos miembros, y queda:
23,074° ≅ θ.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 21/4/18Primero, recuerda que cada recta tiene su propio parámetro, por lo que dejamos k en las ecuaciones cartesianas paramétricas de la primera recta, pero debes asignar otra letra, por ejemplo m, para el parámetro de la segunda recta.
Luego, igualas coordenada a coordenada, y queda el sistema de tres ecuaciones con dos incógnitas:
2 + 2k = -1 + m, aquí sumas 1 en ambos miembros, y queda: 3 + 2k = m (1),
1 - k = -1 + 3m, aquí restas 1 y restas 3m en ambos miembros, y queda: -k - 3m = -2 (2),
3 + k = 4 - 2m, aquí restas 3 y sumas 2m en ambos miembros, y queda: k + 2m = 1 (3).
Luego, sustituyes la expresión señalada (1) en las ecuaciones señaladas (2) (3), y queda el sistema de dos ecuaciones con una incógnita:
-k - 3(3 + 2k) = -2,
k + 2(3 + 2k) = 1;
luego, distribuyes los segundos términos en ambas ecuaciones, reduces términos semejantes, y queda:
-7k - 9 = -2, aquí sumas 9 en ambos miembros, y queda: -7k = 7, divides por -7 en ambos miembros, y queda: k = -1,
5k + 6 = 1, aquí restas 6 en ambos miembros, y queda: 5k = -5, divides por 5 en ambos miembros, y queda: k = -1;
y tienes que el valor del parámetro que corresponde al punto de intersección en la primera recta es: k = -1;
luego, reemplazas el valor remarcado en la ecuación señalada (1), y queda:
3 +2(-1) = m, resuelves y queda: 1 = m,
y tienes que el valor del parámetro que corresponde al punto de intersección en la segunda recta es: m = 1.
Luego, puedes reemplazar en las ecuaciones cartesianas paramétricas que tienes en tu enunciado, y queda:
a)
para la recta r:
x = 2 + 2(-1) = 0,
y = 1 - (-1) = 2,
z = 3 + (-1) = 2;
b)
para la recta s:
x = -1 + 1 = 0,
y = -1 + 3(1) = 2,
z = 4 - 2(1) = 2;
por lo que puedes concluir que el punto de intersección entre las dos rectas queda expresado: A(0,2,2).
Espero haberte ayudado.
-
Hola! Podríais resolverme este ejercicio?
Dada la recta que pasa por P=(-2 , 5) y tiene como pendiente 4/3, calcula las distintas ecuaciones de la recta: vectorial, paramétricas, continua, explícita y punto pendiente.
Lucía
el 21/4/18 -
Ángel
el 21/4/18DAVID CALO BARRERA
el 21/4/18Ángel
el 21/4/18No estoy seguro de si tienes que justificar de otra forma, pero según el enlace que te he mandado:
Parece que q1 cumple que "es un polinomio de grado 2 con n variables" (en concreto 3). Por lo tanto es forma cuadrática.
Parece que q2 no cumple que "es un polinomio de grado 2 con n variables", porque es de grado 1. Por lo tanto no tiene forma cuadrática.
-
Si A y B son 2 conjuntos que estan incluidos dentro de U:
¿Qué significa n(AB)? Parece una Cardinalidad, pero no entiendo que significa eso. ¿Acaso significa n(A)n(B) ?
Ángel
el 21/4/18He considerado que "n" hace referencia al número de elementos del conjunto y las barras "| |" simbolizan el valor absoluto o cardinal, por lo tanto n( ) = | | en el contexto que creo que te mueves.
n(AB)=
|AB| =
|A||B| =
(n(A))n(B)
**De todos modos manda si quieres una foto del contexto de donde has sacado "n(AB)" para que podamos asegurarte.
Carlos Ul po
el 21/4/18Ángel
el 21/4/18Carlos Ul po
el 21/4/18Aleking
el 21/4/18La C que aparece como superíndice se refiere al complementario del conjunto. Te adjunto un esquema para representar las 4 condiciones que te piden en el enunciado. Las respuestas a los apartados a) y b) son t y d respectivamente. Te pongo solo el resultado para que obtengas tú t y d.
-
Buenas noches, en la función f(x) = x2lnx, ¿cuál sería el punto de inflexión? ¿Tiene alguna asíntota?
¡Muchas gracias!
Ángel
el 21/4/18Hallamos la 2ª derivada:
f(x)=x2lnx -----------> Observa que su dominio es [0,inf)
f´(x)= 2xlnx+x2*(1/x) = 2xlnx +x
f´´(x)= 2lnx+2x*(1/x) +1 = 2lnx+2 +1 = 2lnx+3
Igualamos la 2ª derivada a cero:
f´´(x)=0
2lnx+3=0 -----> lnx= -3/2 -----> x= e-3/2 = 1/(√e3) -----------> Observa que 0 ≤ 1/(√e3) ≤ inf , por lo que está dentro del dominio
Por lo tanto tenemos un CANDIDATO a punto de inflexión.
-------------------------------------------------
Estudiamos el posible punto de inflexión x=1/(√e3) calculando si cambia el valor en f´´(x)entre algún intervalo definido por el hipotético punto y el dominio:
(0,1/(√e3)) -----tomamos un valor aleatorio que esté en el intervalo, por ej. x=0.1------> 2ln(0.1)+3 ------> NEGATIVO
(1/(√e3),inf) -----tomamos un valor aleatorio que esté en el intervalo, por ej. x=1------> 2ln(1)+3 ------> POSITIVO
Por lo tanto hemos ASEGURADO y el valor de la coordenada x del punto de inflexión: x=1/(√e3)
--------------------------------------------------
Solo nos queda hallar el par "y" para determinar completamente el P.I., sustituyendo x=1/(√e3) en f(x):
f(1/(√e3))=
(1/(√e3))2*ln(1/(√e3))=
(1/e3)*lne-3/2 =
(1/e3)*(-3/2) =
-3/(2e3)
CONCLUIMOS QUE TENEMOS UN PUNTO DE INFLEXIÓN EN (1/(√e3),-3/(2e3))