-
Fernanda Sanders
el 5/4/18Hola! Alguien sabe hacer este limite? (limite de x elevado a 2x cuando x tiende a 0)
limx->0 x2x
Gracias!
Antonio
el 5/4/18
Antonio Silvio Palmitano
el 5/4/18Vamos con el desarrollo del colega Antonio.
Tienes el límite:
L = Lím(x→0+) x2x,
tomas logaritmos en ambos miembros (observa que el argumento del límite toma valores estrictamente positivos), y queda:
ln(L) = ln( Lím(x→0+) x2x ),
aplicas la propiedad del límite de una función continua, y queda:
ln(L) = Lím(x→0+) ln(x2x),
aplicas la propiedad del logaritmo de una potencia, y queda:
ln(L) = Lím(x→0+) 2x*lnx,
expresas al primer factor lineal como potencia con exponente negativo, y queda:
ln(L) = Lím(x→0+) 2*lnx/x-1;
luego, observa que el numerador tiende a -infinito y que el denominador tiende a +infinito, por lo que para salvar la indeterminación aplicas la Regla de L'Hôpital (derivas independientemente el numerador y el denominador), y queda:
ln(L) = Lím(x→0+) 2*(x-1)/(-x-2);
resuelves el signo y resuelves la división entre potencias con bases iguales, y queda:
ln(L) = Lím(x→0+) -2*x;
resuelves el límite, y queda:
ln(L) = 0 (con x tendiendo a cero desde valores negativos);
luego, compones en ambos miembros con la función inversa del logaritmo natural, y queda:
L = e0;
resuelves el segundo miembro, y queda:
L = 1.
Espero haberte ayudado.
-
Usuario eliminado
el 5/4/18Hola, necesitaría ayuda con este problema:
Un estudiante hace dos pruebas el mismo día. La probabilidad de que pase la primera prueba es de 0’6. La de que pase la segunda es de 0’8 y la de que pase ambas es de 0’5.
-Calcular la probabilidad de que no pase ninguna
-Calcular la probabilidad de que pase la segunda si no ha superado la primera.
-
Rafael S.
el 5/4/18"En una tienda de deportes se han vendido 500 balones de baloncesto, nuevos y usados, y se han obtenido en total 10406 euros. Los balones nuevos se vendieron a 22 euros y los balones usados con descuentos de 20% y 30%. Se sabe que el número de balones usados vendidos ha sido la cuarta parte que los balones nuevos.
a) Plantear un sistema de ecuaciones para hallar el número de balones nuevos que se han vendido
b) Calcular cuántos balones usados se vendieron con descuento del 20%"
¿me podéis ayudar por favor? No tengo ni idea como empezar el ejercicio. O si podéis recomendarme los videos que pueda ver para aclararme
Gracias
Antonio
el 5/4/18Te ayudo a plantear el sistema, lo de resolverlo te lo dejo a ti:
Sea x el número de balones nuevos que se han vendido
Sea y los balones usados que se han vendido con un 20% de descuento
Sea z los balones usados que se han vendido con un 30% de descuento
tenemos, por tanto, que x+y+z=500
Si a el precio de cada balón nuevo es de 22 euros, tenemos que los usados se vendieron a 17.6 y a 15.4 euros respectivamente
y, por lo tanto, tenemos que 22x+17.6y+15.4z=10406
y por ultimo x/4 = y+z
-
Adela García
el 5/4/18necesito ayuda con trigonometria por favor, que tengo examen:
- Calcula de forma exacta cos (15π/4) indicando el numero de vueltas completas y a que cuadrante corresponde el angulo
- Sabiendo que sen α= 3/5 y siendo α un angulo agudo, calcula el resto de razones trigonometricas.
- Teniendo en cuenta el apartado anterior, calcula las siguientes razones:
Cos (180
+
α)sen (-α)
-
Lucia Serrano
el 5/4/18Me podeis ayudar con estos ejercicios:
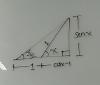
1- Calcula la altura de una casa sabiendo que al tender un cable de 9 m. desde el tejado, se forma un angulo de 60 grados con el suelo. ¿A que distancia de la casa caerá el cable?
2- Lucia esta en la orilla de un rio y observa un arbol que esta en la orilla contraria. Mide el angulo que forma su visual con el punto mas alto del arbol y obtiene 35 grados; retrocede 5 m. y mide otra vez el angulo, obteniendo 25 grados. Calcula la altura del arbol y la anchura del rio.
-
Pedro Matas Rubio
el 5/4/18Una pregunta de probabilidad. Muchas gracias.
En la sala de pediatría de un hospital, el 60% de los pacientes son niñas; de los niños el 35% son menores de 24 meses. El 20% de les niñas tienen menos de 24 meses. Una pediatra que entra en la sala selecciona un paciente al azar:
Determinar el valor de la probabilidad que sea menor de 24 meses y niña.
Determinar el valor de la probabilidad que sea menor de 24 meses.
Si el paciente resulta ser menor de 24 meses, determinar la probabilidad que sea una niña.
-
Juan C
el 5/4/18hola, que tal !.Cómo es la forma de atacar a este ejercicio ?. Llevo tiempo pensándolo, pero a la final... no resulta. Sería de gran ayuda, si un alma noble atiende a mi cuestión. Cómo se procede ante este problema ? necesito ayuda con esta integral !. Gracias por su atención.
-
Lucia
el 5/4/18Hola, me pueden ayudar con un problema de progresiones?
Un agricultor debe echar un cubo de agua a cada uno de los veinte árboles que hay en su huerto.
Estos están alineados a distancias regulares de 6m a lo largo de un camino y la distancia del primer árbol a la fuente es de 12m.
a- Si cada vez lleva un cubo, ¿qué distancia habrá recorrido hasta regar los 20 árboles y dejar el cubo en su posición inicial, junto a la fuente?
b- ¿ Y si llevara dos cubos en cada viaje?
Muchas gracias. Saludos
Antonio Silvio Palmitano
el 5/4/18a)
Para regar el primer árbol recorre (ida más vuelta):
d1 = 12 + 12 = 24 = 24 + 12*0 = 24 + 12*(1-1).
Para regar el segundo árbol recorre (ida más vuelta):
d2 = 12+6 + 12+6 = 24 + 12 = 24 + 12*1 = 24 + 12*(2-1).
Para regar el tercer árbol recorre (ida más vuelta):
d3 = 12+6+6 + 12+6+6 = 24 + 24 = 24 + 12*2 = 24 + 12*(3-1).
Para regar el cuarto árbol recorre (ida más vuelta):
d4 = 12+6+6+6 + 12+6+6+6 = 24 + 36 = 24 + 12*3 = 24 + 12*(4-1).
Luego, puedes inferir la expresión de la distancia recorrida para regar al árbol número k (ida y vuelta)
dk = 24 + 12*(k-1), con k ∈ N, 1 ≤ k ≤ 20,
que es la expresión del elemento general de una progresión aritmética,
cuyo primer elemento es: d1 = 24,
cuya diferencia es: D = 12,
y cuyo último elemento es:
d20 = 24 + 12*(20-1) = 24 + 12*19 = 24 + 228 = 252.
Luego, planteas la expresión de la suma de los veinte elementos de la progresión aritmética, y queda:
S20 = (d1 + d20)*20/2 = (24 + 252)*10 = 276*10 = 2760;
por lo que tienes que la distancia total que recorrió el agricultor es 2760 metros.
Espero haberte ayudado.
Antonio Silvio Palmitano
el 5/4/18Observa que ahora debe realizar diez viajes (ida y vuelta), ya que en cada viaje puede regar dos árboles.
Luego, vamos planteando las distancias recorridas en forma similar al caso anterior:
Viaje 1 (para regar los árboles 1° y 2°):
p1 = 12+6 + 12+6 = 36 = 36 + 24*0 = 36 + 24*(1-1).
Viaje 2 (para regar los árboles 3° y 4°):
p2 = 12+6+6+6 + 12+6+6+6 = 60 = 36 + 24 = 36 + 24*1 = 36 + 24*(2-1).
Viaje 3 (para regar los árboles 5° y 6°):
p3 = 12+6+6+6+6+6 + 12+6+6+6+6+6 = 84 = 36 + 48 = 36 + 24*2 = 36 + 24*(3-1).
Luego, puedes inferir la expresión de la distancia recorrida en el viaje número k:
pk = 36 + 24*(k-1), con k ∈ N, 1 ≤ k ≤ 10,
que es la expresión del elemento general de una progresión aritmética,
cuyo primer elemento es: p1 = 36,
cuya diferencia es: D = 24,
y cuyo último elemento es:
p10 = 36 + 24*(10-1) = 36 + 24*11 = 36 + 264 = 300.
Luego, planteas la expresión de la suma de los veinte elementos de la progresión aritmética, y queda:
S10 = (p1 + p10)*10/2 = (36 + 300)*5 = 336*5 = 1680;
por lo que tienes que la distancia total que recorrió el agricultor es 1680 metros.
Espero haberte ayudado.
-
Lsslie
el 5/4/18 -
amalia
el 5/4/18
