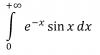-
Hola buenas tardes estaba haciendo esta integral impropia pero lo malo es que cuando tengo que evaluarlo en infinito no se como actua los senos y cosenos al infinito
i me pudieran enseñar graficamente como actuan seno y coseno al x tender a infinito se los agradeceria mucho, o si es por medio de otro metodo
Ángel
el 5/3/18El seno y el coseno con funciones periódicas (y no constantes) que no tienen límite en el infinito.
Van tomando una serie de valores hasta llegar al valor de inicio y seguirán el ciclo hasta el infinito...
Antonio Silvio Palmitano
el 5/3/18Vamos por pasos.
1°)
Plantea la integral indefinida:
I1 = ∫ e-x*senx*dx, aplicas el Método de Integración por Partes (te dejo la tarea), y queda:
I1 = -e-x*senx + ∫ e-x*cosx*dx, aplicas el Método de Integración por partes en la integral secundaria (te dejo la tarea), y queda:
I1 = -e-x*senx - e-x*cosx - ∫ e-x*senx*dx, sustituyes la expresión del último término (observa que tienes la integral inicial), y queda:
I1 = -e-x*senx - e-x*cosx - I, haces pasaje de término, extraes factor común, y queda:
2*I1 = -e-x*(senx + cosx), multiplicas en ambos miembros por 1/2, y queda:
I1 = -(1/2)*e-x*(senx + cosx) + C, aplicas la propiedad de las potencias con exponente negativo en el segundo factor, y queda:
I1 = -(1/2)*(senx + cosx)/ex + C.
2°)
Plantea la integral definida entre 0 y un valor genérico b:
I2 = 0∫b e-x*senx*dx = sustituyes = [ -(1/2)*(senx + cosx)/ex ], evalúas con Regla de Barrow, y queda:
I2 = -(1/2)*(senb + cosb)/eb - ( -(1/2)*(sen0 + cos0)/e0 ), reemplazas valores y resuelves el signo en el segundo término, y queda:
I2 = -(1/2)*(senb + cosb)/eb + 1/2, distribuyes el primer término, y queda:
I2 = -(1/2)*senb/eb - (1/2)*cosb/eb + 1/2.
3°)
Plantea el límite para b tendiendo a + infinito de esta última expresión, y tienes para la integral impropia de tu enunciado:
I = Lím(b→+∞) ( -(1/2)*senb/eb - (1/2)*cosb/eb + 1/2 );
luego, resuelves término a término (observa que en los dos primeros términos tiene expresiones acotadas entre -1 y 1 en los numeradores, y expresiones que tienden a +infinito en los denominadores, y observa que el tercer término es constante), y queda:
I = ( -0 - 0 + 1/2 ) = 1/2.
Espero haberte ayudado.
-
Comprobar que
r= (x-2)/2 =(y-3)/3 = (z-4)/4
y r'= (x-1)/2 = (y-2)/-1 = (z-3)/-4
están en un mismo plano y hallar su ecuacion
Gracias
Antonio Silvio Palmitano
el 5/3/18Tienes las ecuaciones cartesianas simétricas (o continuas) de dos rectas, cuyos vectores directores son (recuerda que las componentes de los vectores directores las tienes en los denominadores):
u = <2,3,4> (vector director de la recta r),
u ' = <2,-1,-4> (vector director de la recta r ').
Luego, si las rectas están incluidas en un mismo plano, puedes plantear que un vector normal al plano es el producto vectorial entre los vectores directores de las rectas:
n = u x u ' = <2,3,4> x <2,-1,-4> = <-8,16,-8>.
Luego, tienes las coordenadas de un punto de cada recta (recuerda que las tienes restando en los numeradores):
A(2,3,4) que pertenece a la recta r,
A' (1,2,3) que pertenece a la recta r '.
Luego, con el vector normal (n) y el punto A, puedes plantear la ecuación del plano que contiene a la recta r:
-8*(x-2) + 16*(y-3) - 8*(z - 4) = 0, distribuyes en todos los términos, reduces términos numéricos, y queda:
-8*x + 16*y - 8*z = 0, divides en todos lo.s términos de la ecuación por -8, y queda:
x - 2*y + z = 0.
Luego, observa que el punto A ' pertenece a este plano porque sus coordenadas verifican su ecuación,
por lo que tienes que la recta r y la recta r ' están incluidas en el plano cuya ecuación cartesiana hemos remarcado.
Espero haberte ayudado.
Rasyer
el 5/3/18Primero tenemos que saber que dos rectas forman un plano solamente si
se cortan o si son paralelas. Si son coincidentes o se cruzan no forman
un plano.Pasamos las rectas que se encuentran en forma contínua a equaciones implícitas:
r =
3x - 2y = 0
2x - z = 0
r' =
-x -2y +5 = 0
-2x -z + 5 = 0
Ahora hacemos una matriz con las ecuaciones de las rectas en las filas y hacemos gauss:
3 -2 0 | 0
2 0 -1 | 0-1 -2 0 | -5
-2 0 -1 | -5
El
resultado es un sistema compatible determinado. Esto quiere decir que
las rectas se cortan en un punto. Si las rectas se cortan forman un
plano.Para formular la ecuación de un plano simplemente
necesitamos un punto y dos vectores directores. El punto puede ser
cualquier punto de una de las dos rectas. Los vectores directores seran
los vectores de las rectas.Punto: (1, 2, 3) ( forma parte de la recta r' )
Vectores:
Si tenemos la ecuación contínua es muy fácil encontrar los vectores directores.
v1 = (2, 3, 4) (vector de la recta r)
v2 = (2, -1, -4) (vector de la recta r')
Ahora construimos paso a paso la ecuación del plano:
(x,y,z) = (1,2,3) + λ(2,3,4) + μ(2,-1,-4)
-
x = 1 + λ2 + μ2
y = 2+ λ3 - μ
z = 3 + λ4 - 4μ
Ahora tienes que resolver el determinante (aunque personalmente me parece más rápida la manera de Antonio, encontrando el vector normal)
| x-1 y-2 z-3 |
| 2 3 4 | = -8x + 16y − 8z = x - 2y - z
| 2 -1 - 4 |
-
le directeur commercial affirme que 80% desnconsommateurs sont satisfaits de la qualite des produits commercialises par son enterprise.On realise une etude de satisfaction sur un echantillon de 120 personnes interrogees. 87 declarent etre satisfaites des produits Determiner en justifiant si l on doit remettre en question l affirmation du directeur commercial
no se como hacer este ehjercicio respondanme lo antes posible por favor
Ángel
el 5/3/18le directeur commercial affirme que 80% desnconsommateurs sont satisfaits
Etude de satisfaction= [ (87 personnes satisfaites)÷(120 personnes interrogees) ] × 100
Etude de satisfaction= [ 0.725 ] × 100
Etude de satisfaction= 72.5 %
El director comercial es demasiado optimista, hay un 7.5% menos de clientes satisfechos que los que él cree.
-
Buenas, sigo atascado con esta derivada implícita, sé que debo usar la derivación logarítmica pero simplemente no llego al Resultado, o sea, me pierdo en el procedimiento.
y(e)2x +(X)2y =1
Respuesta y'=-e2-2
Ese es el enunciado, pues es un simple ejercicio de práctica.
Antonio Silvio Palmitano
el 5/3/18Te ayudo con la derivación.
Recuerda la identidad: x = elnx (1).
Luego, sustituyes la expresión señalada (1) en el segundo término de la ecuación, y queda:
y*e2x + (elnx)2y = 1.
Luego, aplicas la propiedad de una potencia cuya base es otra potencia en el segundo término, y queda:
y*e2x + e2y*lnx = 1.
Luego, derivas término a término (recuerda que y es una función que depende de x, y observa que debes aplicar la Regla de la Cadena), y queda:
y ' * e2x + y * 2*e2x + e2y*lnx * ( 2*y ' * lnx + 2 *y * (1/x) ) = 0.
Luego, distribuyes el tercer término, ordenas factores en los términos, y queda:
y ' * e2x + 2*y * e2x + y ' * 2*lnx*e2y*lnx + 2*(y/x)*e2y*lnx = 0.
Luego, haces pasajes de términos, y queda:
y ' * e2x + y ' * 2*lnx*e2y*lnx = -2*y * e2x - 2*(y/x)*e2y*lnx.
Luego, extraes factores comunes en ambos miembros, y queda:
y ' * ( e2x + 2*lnx*e2y*lnx ) = -2*(y/x) * ( x*e2x + e2y*lnx ).
Luego, haces pasaje de factor como divisor, y queda:
y ' = -2*(y/x) * ( x*e2x + e2y*lnx ) / ( e2x + 2*lnx*e2y*lnx ).
Luego, resuelves el numerador y el denominador, y queda:
y ' = -2*y*( x*e2x + e2y*lnx ) / x*( e2x + 2*lnx*e2y*lnx ),
y observa que deben cumplirse las condiciones:
x > 0,
e2x + 2*lnx*e2y*lnx ≠ 0.
Con respecto a la respuesta, por favor verifica que esté completa en tu enunciado.
Espero haberte ayudado.
-
daniel mayo
el 5/3/18si x, = (1,-1,3) e y, = (α,2,-2)
hallar 2x, -3y, es:
2(1,-1,3) - 3(α, 2,-2)=
= (2, -2, 3) - (3α, 6 -6)= (2-3α, -8, 9)
hallar el valor de α para que x, y,=10 es :
x,y,=10
(1,-1,3)(α,2,-2)=10
(1.α+(-1).2+3.(-2)=10
(α-2+6)=10
α+4=10
α=10-4=6
y para hacer x,-y, = (5,-3,5)
(1,-1,3) - (α,2,-2)= (5,-3,5)
(1-α, -3, 3-(-2))=( 5,-3-5)
(1-α, -3, 5) = (5, -3,-5) de haca saco que 1-α=5 -----------> -α=5-1----> α= -4
y para el segundo punto es un sistema de ecuaciones de 2x2:
me quedaria :
4α-β=1
-5α =3 estas dos ecuaciones entre llaves
de la segunda ecuacion saco que α=-3/5 lo suplanto en la primera 4(-3/5) - β=1
(-12/5)-β=1
-β=1+12/5-------------> -β=17/5-------------------------------->β=-17/5
-
Antonio Silvio Palmitano
el 6/3/18Haces pasaje de término, y tu ecuación diferencial queda:
y2+1 = y*e-x*dy/dx, multiplicas en ambos miembros por ex (observa que es una expresión que es estrictamente positiva), y queda:
(y2+1)*ex = y*dy/dx, luego, separas variables, tal como indica el colega Eduardo, y queda:
ex*dx = y*dy/(y2+1),
integras en ambos miembros (observa que en el primero es directa, y en el segundo que puedes aplicar la sustitución (cambio de variable): w = y2+1), y queda:
ex + C = (1/2)*ln(y2+1) (1),
que es una ecuación implícita que expresa la solución general de la ecuación diferencial;
luego, evalúas para la condición inicial que tienes en tu enunciado (x = 0, y = 0), y queda:
1 + C = 0, haces pasaje de término, y queda: C = -1;
luego, reemplazas en la ecuación señalada (1), y queda:
ex - 1 = (1/2)*ln(y2+1),
que es una ecuación implícita que expresa la solución particular de la ecuación diferencial;
para la condición inicial que tienes en tu enunciado (x = 0, y = 0).
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 5/3/18Observa que tienes un campo vectorial F = < P , Q> cuyas componentes (P y Q) son funciones continuas y tienen derivadas parciales primeras continuas en R2.
Luego, tienes para las componentes del campo:
P = y*exy, cuyas derivada parcial con respecto a y queda:
Py = 1*exy + y*x*exy = (1+x*y)*exy;
Q = 1 + x*exy, cuyas derivada parcial con respecto a x queda:
Qx = 0 + 1*exy + x*y*exy = (1+x*y)*exy;
luego, como tienes que las expresiones de las derivadas parciales que hemos calculado son iguales, puedes concluir que el campo vectorial es conservativo, y admite función potencial.
Luego, plantea la relación entre la función potencial y su campo conservativo asociado:
∇g = F, sustituyes las expresiones del gradiente de la función potencial y del campo conservativo, y queda:
< gx , gy > = < P , Q >;
luego, por igualdad entre vectores, tienes el sistema de ecuaciones diferenciales (observa que sustituimos las expresiones de las componentes del campo):
gx = y*exy, aquí integras parcialmente con respecto a x, y queda: g(x,y) = exy + A(y) (1);
gy = 1 + x*exy, aquí integras parcialmente con respecto a y, y queda: g(x,y) = y + exy + B(x);
luego, tienes la expresión de la familia de funciones potenciales (observa que la formas con los términos explícitos sin repetirlos y le sumas una constante arbitraria):
g(x,y) = y + exy + C,
y puedes verificar que sus derivadas parciales se corresponden con las componentes del campo conservativo.
Luego, tienes la expresión de la función vectorial de posición de los puntos de la trayectoria:
γ(t) = < 2*t-1 , t2-t >, con t ∈ [0,1];
luego, evalúas la posición inicial y la posición final de la partícula, y queda:
γ(0) = < -1 , 0 >, por lo que tienes que la partícula se encuentra en el punto inicial de la trayecoria: A(-1,0),
γ(1) = < 1 , 0 >, por lo que tienes que la partícula se encuentra en el punto final de la trayectoria: B(1,0).
Luego, aplicas el Teorema Fundamental de las Integrales de Línea, y tienes para el trabajo del campo:
WF = ∫γ F*dr = aplicas el teorema = [ g(x,y) ], para evaluar entre el punto A(-1,0) y B(1,0);
luego, sustituyes la expresión de la función potencial (observa que no necesitas la constante por ser una integral definida), y queda:
WF = [ y + exy ] = evalúas = ( 0 + 1 ) - ( 0 + 1) = 1 - 1 = 0.
Espero haberte ayudado.
-
Ángel
el 5/3/18a)
Vamos a interpretar la tabla:
2 sacaron un 4 estudiando 6 horas
1 sacó un 4 estudiando 7 horas
3 sacaron un 5 estudiando 7 horas
1 sacó un 5 estudiando 8 horas
1 sacó un 6 estudiando 8 horas
2 sacaron un 6 estudiando 9 horas
Para aprobar, en tu tabla la nota Y ha de ser 5 o 6 .
Nº medio de horas que dedicaron los aprobados= (suma de las horas que dedicaron los aprobados)/ nº de aprobados
Nº medio de horas que dedicaron los aprobados= (3*7+1*8+1*8+2*9)/(3+1+1+2) = (21+8+8+18)/7 = 55/7 = 7.86 horas
-----------------
Suspensos= (3suspensos/10presentados)*100 = 30%
Aprobados= (7aprobados/10presentados)*100 = 70%
Rasyer
el 5/3/18Ángel
el 8/3/18Para el apartado b) tienes que utilizar recta de regresión lineal:
https://www.youtube.com/watch?v=Jwulx_AvVBc
Si después de ver el vídeo e intentarlo no te sale, nos dices y te lo resolvemos.