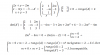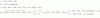-
Angela
el 6/3/18 -
Alejandro Ballesteros
el 6/3/18
Pueden resolver cualquiera de estos? Muchas gracias
Antonius Benedictus
el 6/3/18¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
sheyla
el 6/3/18 -
Usuario eliminado
el 6/3/18Hola buenas, no tengo ni idea de por donde empezar en este ejercicio. Considere la recta r del espacio que pasa por el punto P = (1, 1, 3) y tiene por vector director v = (1 -a, a, 1). Sea π el plan que tiene por ecuación 2x + y - z = 1. A) Determine para cada valor del parámetro a la posición relativa de la recta r respecto al plano π (paralela, contenida o con un punto de intersección). B )Hay alguna de las rectas r que sea perpendicular al plano π?
Muchas gracias
Antonio Silvio Palmitano
el 7/3/18Observa que el punto P pertenece a la recta, pero observa que no pertenece al plano.
Tienes la expresión general del vector director de la recta: u = <1-a,a,1>.
Tienes un vector normal al plano: n = <2,1,-1>.
a)
Plantea la condición de paralaelismo entre recta y plano: los vectores directores de la recta son perpendiculares a los vectores normales al plano, y el producto escalar entre ellos es igual a cero, por lo que puedes plantear:
n • u = 0, sustituyes expresiones, y queda:
<2,1,-1> • <1-a,a,1> = 0, desarrollas el producto escalar, y queda la ecuación:
2(1-a) + a - 1 = 0, resuelves (te dejo la tarea), y queda: a = 1,
y observa que como el punto P pertenece a la recta y no pertenece al plano, tienes que para a = 1 la recta es paralela exterior al plano, y no está contenida en él.
b)
Plantea la condición de perpendicularidad entre recta y plano: los vectores directores de la recta son paralelos a los vectores normales al plano, y el producto vectorial entre ellos es igual al vector nulo (N), por lo que puedes plantear:
n x u = N, sustituyes expresiones, y queda:
<2,1,-1> x <1-a,a,1> = <0,0,0>, desarrollas el producto vectorial en el primer miembro, y queda:
<1+a,a-3,3a-1> = <0,0,0>;
luego, por igualdad entre vectores, igualas componente, y queda el sistema de ecuaciones
1 + a = 0, aquí haces pasaje de término, y queda: a = -1 (1),
a - 3 = 0, aquí haces pasaje de término, y queda: a = 3 (2),
3a - 1 = 0, aquí haces pasaje de término, y luego pasaje de factor como divisor, y queda: a = 1/3 (3),
y como los valores señalados (1) (2) (3) son distintos, tienes que el sistema de ecuaciones no tiene solución, por lo que tienes que no existe un valor real del parámetro para el cuál la recta y el plano sean perpendiculares.
c)
Para todo valor del parámetro que sea distinto de 1, tienes que la recta y el plano se cortan en un punto.
Espero haberte ayudado.
-
Jordi García
el 6/3/18¿Cómo discuto un sistema de tres ecuaciones con dos incógnitas que depende de un parámetro? Comparando rangos si puede ser.
Sistema:
2x + y = 2m
x - my = -3
x + y = 3
Gracias.
Usuario eliminado
el 6/3/18 -
A
el 6/3/18 -
Adria Berbis Cobo
el 6/3/18 -
Gabriel Lopez Calderon
el 6/3/18Hola, hice una pregunta pero no me quedo del todo clara la respuesta.
Lo que quiero saber es cual es el "Teorema del valor medio del claculo integral" puesto que me estoy preparando para un examen y esa es una pregunta de Final. Me se el de Rolle, Lagrange, Bolzano, Cauchy y me falta ese "Teorema del valor medio del calculo integral". Cada uno con su respectiva intepretacion geometrica -
Ana Belen Corredor
el 6/3/18hola. Necesito cursar dos asignaturas para habilitarme. Alguien podría decirme que dos asignaturas son más asequibles teniendo en cuenta que vengo de una carrera de Ciencias Ambientales?
gracias.
-
Gabriel Lopez Calderon
el 6/3/18Hola, queria preguntar si alguien tiene un video o algo que explique el teorema del valor medio del calculo integral (con una interpretación geométrica) y que diferencias hay con el teorema del valor medio de Lagrange y Rolle. Gracias!
