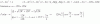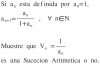-
Alguien sabe como resolver estos problemas?
De las 5 llaves que Laura tiene en el llavero, necesita dos para entrar en su casa. Si pierde 2 de las 5 llaves, ¿cuál es la probabilidad de que Laura no pueda entrar a su casa?
Las dimensiones de una hoja A4 son 21 cm 29,7 cm. En una práctica de papiroflexia una de ellas ha sido plegada de modo que uno de sus vértices coincide con su opuesto. Calcula el área del polígono resultante.
Rasyer
el 7/3/18No estoy muy de acuedo contigo Fran, en mi opinión lo haría así:
En el primer problema Laura no podrá entrar en su casa si pierde una de las llaves, o las dos. Fíjate que para resolverlo no nos importa si primero piede una y después la otra, no importa el orden. Para resolverlo lo podemos hacer al contrario, calculando cuantas posibilidades tiene de entrar a casa. Para que esto suceda Laura tiene que perder 2 de las 3 llaves que no le sirven para entrar. Para calcular elegimos una de las 3 llaves (sobre un total de 5), y luego una de las dos llaves malas (sobre un total de 4). El resultado es 3/5 * 2/4 = 3/10. Estas son las posibilidades que entre a casa. Por lo tanto las posibilidades que no entre a casa son 1- (3/10) = 7/10
En el segundo problema el área se calcula base por altura. b*a. Date cuenta que es indiferente dividir entre dos la base o la altura porque b*(a/2) = (b*a)/2, y (b/2)*a = (b*a)/2
Por lo tanto, el resultado es 10.5 * 29.7 = 21 * 14.85 = 311.85 cm²
--
Si el primer problema no te queda lo puedes hacer con la regla de Laplace. Los casos favorables entre los posibles. Vamos a llamas las llaves 1, 2, 3, 4, 5. Las buenas son la 1 y la dos.
Casos posibles: 1,2 1,3 1,4 1,5 2,3 2,4 2,5 3,4 3,5 4,5
Casos favorables: 1,2 1,3 1,4 1,5 2,3 2,4 2,5
Probabilidad: 7/10
Fran Devesa Peiró
el 7/3/18 -
Me podeis ayudar con este problema?
En Villacastaños están celebrando una fiesta medieval. Dos comerciantes llegan al puesto aduanero llevando 64 y 20 barriles de cerveza respectivamente. Como no tenían dinero suficiente para pagar los derechos de aduana, el primero de ellos dio 5 barriles y 40 monedas, mientras que el segundo dio 2 barriles, recibiendo 40 monedas como cambio. ¿Cuál era el precio de cada barril y su impuesto aduanero?
Antonio Silvio Palmitano
el 7/3/18Puedes llamar x al precio de cada barril.
Luego, plantea la razón entre las cantidades de barriles de los comerciantes:
rc = 60/20 = 3 (1).
Luego, plantea la razón entre las sumas de dinero pagadas como derechos de aduana por los comerciantes:
rd = (5x+40) / (2x-40).
Luego, como las sumas abonadas son proporcionales a las cantidades de barriles de los comerciantes, puedes plantear que las razones son iguales, y queda la ecuación:
rc = rd, sustituyes expresiones, y queda:
3 = (5x+40) / (2x-40), haces pasaje de divisor como factor, y queda:
3(2x-40) = 5x + 40, distribuyes el primer miembro, y queda:
6x - 120 = 5x + 40, haces pasajes de términos, reduces términos semejantes, y queda:
x = 160, que es el precio de un barril;
luego, planteas las expresiones de las sumas de dinero abonadas en concepto de derechos aduaneros, y quedan:
y1 = 5x + 40 = 5(160) + 40 = 800 + 40 = 840;
y2 = 2x - 40 = 2(160) - 40 = 320 - 40 = 280;
y observa que la razón entre las sumas de dinero abonada queda:
rs = y1/y2 = 840/280 = 3.
Espero haberte ayudado.
-
Buenos días !! Necesito que me expliquen como construir triangulos.
¿como construir un triángulo isosceles dónde ab=bc, ac=3cm y b=20°
Fran Devesa Peiró
el 7/3/18Las propiedades de un triángulo isósceles son que dos lados son iguales (ab=bc) y que dos de sus ángulos son idénticos entre sí. En este caso te dan que el ángulo es 20º, y sabemos que la suma de los ángulos de cualquier triángulo es de 180º. Así pues sólo hay dos opciones:
a) Los dos ángulos son de 20º y hay un tercero que: 180=20+20+x, por lo que 180-20-20=x . Siendo el ángulo de 140º
b) Los dos ángulos son los complementarios al dato que tenemos que es 20º. Por lo que tenemos un sistema de ecuaciones donde x=y (siendo x e y los ángulos que necesitamos) y que 180=x+y+20; de aquí obtenemos que 180=x+x+20, o lo que es lo mismo 180-20=2x, de donde tenemos finalmente que 160/2=70=x. De aquí obtenemos que los dos ángulos que necesitamos para construir nuestro triángulo son cada uno de 80º.
En este caso la opción es la b, ya que si te dibujas los vértices que te dan b=20º que es el único que es diferente puesto que ac= 3cm
Una vez tenemos esto con trigonometría obtenemos todos los datos que necesitamos, aquí hay dos opciones igual de válidas.
a) descomponemos el triángulo en dos partes simétricas entre sí, (el ángulo que era dato pasa a ser 10º y el lado dado pasa a ser 3/2=1,5 cm,de aquí con el cos 80º= 1.5/x despejamos y obtenemos que x=1.5/cos80 = 8.64 cm
b) con el teorema del seno: 1.5/sin20 = x/sin 80, despejando obtenemos que x=1.5*sin(80)/sin(20)=8.64 cm

-
Antonio Silvio Palmitano
el 7/3/18Tienes la expresión del elemento general de la sucesión V expresado en función del elemento general de la sucesión A:
Vn = 1/an, haces pasaje de divisor como factor, luego de factor como divisor, y queda: an = 1/Vn (1);
luego, planteas la expresión del elemento general siguiente, y queda:
Vn+1 = 1/an+1, haces pasaje de divisor como factor, luego de factor como divisor, y queda: an+1 = 1/Vn+1 (2).
Tienes la definición en forma recursiva del elemento general siguiente de la sucesión A:
an+1 = an / (1 + an) (3), con a0 = 1, n ∈ N;
luego, sustituyes las expresiones señaladas (1) (2) en la ecuación señalada (3), y queda:
1/Vn+1 = (1/Vn) / (1 + 1/Vn),
extraes denominador común en el segundo agrupamiento, y queda:
1/Vn+1 = (1/Vn) / (Vn + 1)/Vn,
resuelves la división entre expresiones fraccionarias en el segundo miembro (observa que tienes simplificaciones), y queda:
1/Vn+1 = 1 / (Vn + 1),
haces pasajes de divisores como factores, y queda:
Vn + 1 = Vn+1,
haces pasajes de términos, y queda:
1 = Vn+1 - Vn, con V0 = 1/a0 = 1/1 = 1, n ∈ N,
y observa que en la ecuación remarcada tienes que la resta entre el elemento general siguiente y el elemento general es una constante (que es 1 para este ejercicio), lo que es característico en las sucesiones aritméticas,
por lo que puedes concluir que la sucesión V es aritmética, con primer elemento 0 y diferencia 1.
Espero haberte ayudado.
-
Con los digitos 4,5,6y7.
cuantos numeros de tres cifras menores que 600 se puede escrbir.
cuantos numeros impares de tres cifras impares se puede escribir.
cuantos numeros de tres cifras impares y menores que 600 se pueden escrbir.
Antonio Silvio Palmitano
el 7/3/18a)
Observa que puedes repetir cifras.
Eliges la primera cifra (que puede ser 4 o 5), por lo que tienes: A = 2 opciones.
Eliges la segunda cifra (que puede ser cualquiera de las cuatro), por lo que tienes B = 4 opciones.
Eliges la tercera cifra (que puede ser cualquiera de las cuatro), por lo que tienes C = 4 opciones.
Luego, por el principio de multiplicación, tienes:
a = A*B*C = 2*4*4 = 32 número menores que 600, formados con tres cifras.
b)
Observa que puedes repetir cifras.
Eliges la primera cifra (que puede ser 5 o 7), por lo que tienes: A = 2 opciones.
Eliges la segunda cifra (que puede ser 5 o 7), por lo que tienes B = 2 opciones.
Eliges la tercera cifra (que puede ser 5 o 7), por lo que tienes C = 2 opciones.
Luego, por el principio de multiplicación, tienes:
a = A*B*C = 2*2*2 = 8 números impares formados con tres cifras impares.
c)
Observa que puedes repetir cifras.
Eliges la primera cifra (que debe ser 5), por lo que tienes: A = 1 opción.
Eliges la segunda cifra (que puede ser 5 o 7), por lo que tienes: B = 2 opciones.
Eliges la tercera cifra (que puede ser 5 o 7), por lo que tienes C = 2 opciones.
Luego, por el principio de multiplicación, tienes:
a = A*B*C = 1*2*2 = 4 números menores que 600 formados con tres cifras impares.
Espero haberte ayudado.
-
Hola unicoos porfavor ayudenme, no le estoy entendiendo a mi materia de probabilidad y necesito resolver este ejercicio me pueden explicar o recomendar algunos videos de probabilidad porfavor
Antonio Silvio Palmitano
el 7/3/18Observa que tienes: x = 12 min = 12/60 = 1/5 = 0,2 hora.
a)
p(X<0,2) = F(0,2) = 1 - e-8*0,2 = 1 - e-1,6 ≅ 0,7981.
b)
Recuerda que la derivada de la función de distribución de probabilidad F es la función de densidad de probabilidad f.
Luego, derivas, y la expresión de la función de densidad de probabilidad queda:
f(x) = F ' (x) =
0 si x ≤ 0,
8*e-8x si x > 0.
Luego, planteas:
p(X<0,2) = -∞∫0,2 f(x)*dx =
= -∞∫0 0*dx + 0∫0,2 8*e-8x*dx =
= 0 + 8*0∫0,2 e-8x*dx =
= 8 * [ -(1/8)*e-8x ] = evalúas con Regla de Barrow:
= 8 * ( -(1/8)*e-8*0,2 - (-(1/8)*e-8*0) ) =
= 8 * ( -(1/8)*e-1,6 + (1/8)*1 ) =
= 8*(1/8) * ( -e-1,6 + 1 ) = simplificas los dos primeros factores
= 1 - e-1,6 ≅ 0,7981.
Espero haberte ayudado.
-
Determina si el vector (x,y) es combinación lineal de los vectores u=(2,-3) y v=(3,6). ¿Cómo sigo cuando tengo dos incógnitas?

Antonio Silvio Palmitano
el 7/3/18Has planteado correctamente la combinación lineal, y has obtenido el sistema de ecuaciones
2a1 + 3a2 = x,
-3a1 + 6a2 = y.
a)
Multiplicas por 2 en todos los términos de la primera ecuación, mantienes la segunda ecuación, y queda:
4a1 + 6a2 = 2x,
-3a1 + 6a2 = y;
luego, restas miembro a miembro (observa que tienes cancelaciones), y queda:
7a1 = 2x - y, multiplicas por 1/7 en todos los términos, y queda: a1 = (2/7)x - (1/7)y;
b)
Multiplicas por 3 en todos los términos de la primera ecuación, y por 2 en todos los términos de la segunda, y queda:
6a1 + 9a2 = 3x,
-6a1 + 12a2 = 2y;
luego, sumas miembro a miembro (observa que tienes cancelaciones), y queda:
21a2 = 3x + 2y, multiplicas por 1/21 en todos los términos y queda: a2 = (1/7)x + (2/21)y.
Luego, puedes concluir que para cada vector <x,y> existen los escalares a1 y a2, cuyas expresiones tienes remarcadas.
Espero haberte ayudado.
-
Con los digitos 4,5,6y 7.
cuantos numeros de tres cifra menores que 600 se pueden escrbier.
QUIERO SABER SI HAY UNA FORMA RESOLVERLO MAS RAPIDO.
jorge velazquez
el 7/3/18jorge velazquez
el 7/3/18