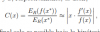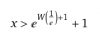-
Hola! Tengo una duda con la siguiente ecuación diferencial:
Xraiz(X2 +1) dx-yey dy=0
Solo se que es de variable separables y que los diferenciales deben de quedar arriba. Lo único que se me ocurre sería pasar el yey dy al otro lado del igual. ¿Ya podría integrar?
Muchas gracias, y espero vuestra respuesta. Saludos!
Antonio Silvio Palmitano
el 8/3/18Tienes la ecuación diferencial:
x*√(x2+1)*dx - y*ey*dy = 0, haces pasaje de término, y queda:
-y*ey*dy = -x*√(x2+1)*dx, multiplicas en ambos miembros por -1, y queda:
y*ey*dy = x*(x2+1)1/2*dx;
luego, observa que tienes las variables separadas, por lo que ya puedes integrar en ambos miembros (observa que en el primer miembro debes aplicar el Método de Integración por Partes, y que en el segundo miembro debes aplicar la sustitución (cambio de variable): w = x2+1), luego integras (te dejo la tarea de plantear las integrales), y queda:
y*ey - ey = (1/3)*(x2+1)3/2 + C;
que es una solución general implícita de la ecuación diferencial de tu enunciado.
Espero haberte ayudado.
-
Hola buenas, alguien me ayuda con estas dos inecuaciones? Gracias de antemano. (perdon por el tamaño de la foto)
Jose
el 8/3/18Jose
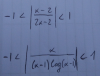
el 8/3/18No, me preguntan si la expresión está bien condicionada. Se utiliza la siguiente fórmula:
Yo he usado la fórmula, y he simplificado y queda lo que mandé en la foto del principio.
Para saber si está bien condicionada tienes que comprobar los valores de x cuando la expresión resultante es <1. Mi problema es al despejar el logaritmo. No se como despejarlo.
Muchas gracias de nuevo.
Antonio Silvio Palmitano
el 8/3/18a)
Observas que debe cumplirse la condición: 2x - 2 ≠ 0, que al despejar queda: x ≠ 1.
Observa que tienes valor absoluto en el miembro central (que, por lo tanto es positivo), por lo que la doble inecuación puedes escribirla en la forma:
0 ≤ |(x-2)/(2x-2)| < 1.
Luego, distribuyes el valor absoluto entre el numerador y el denominador del término central, multiplicas por |2x-2| en todos los miembros de la doble inecuación, y queda:
0 ≤ |(x-2)| < |2x-2|.
Luego, observa que la doble inecuación implica el que dos inecuaciones son válidas al mismo tiempo:
1)
0 ≤ |(x-2)|, que es válida para todo número real:
2)
|(x-2)| < |2x-2|,
que por definición de valor absoluto conduce a cuatro opciones:
2A)
los dos argumentos de los valores absolutos son positivos, lo que conduce a las condiciones: x ≥ 2, x ≥ 1,
y también a: x - 2 < 2x -2, haces pasajes de términos, y queda: -x < 0, multiplicas en ambos miembros por -1 (observa que cambia la desigualdad), y queda la condición: x > 0, por lo que para esta opción tienes el intervalo A = [2,+∞);
2B)
los dos argumentos de los valores absolutos son negativos, lo que conduce a las condiciones: x < 2, x < 1,
y también a: -(x - 2) < -(2x -2), distribuyes, haces pasajes de términos, y queda: x < 0,
por lo que para esta opción tienes el intervalo B = (-∞,0];
2C)
el primer argumento es positivo y el segundo es negativo, lo que conduce a las condiciones: x ≥ 2 y x < 1, que son contradictorias, por lo que para esta opción tienes el intervalo vacío: Φ;
2D)
el primer argumento es negativo y el segundo es positivo, lo que conduce a las condiciones: x < 2 y x ≥ 1,
y también a: -(x - 2) < 2x - 2, distribuyes, haces pasajes de términos, y queda: -3x < -4, divides en ambos miembros de esta inecuación por -3 (observa que cambia la desigualdad), y queda: x > 4/3,
por lo que para esta opción tienes el intervalo: D = (4/3, 2);
3)
tienes que el conjunto solución de la doble inecuación con valor absoluto que tienes en tu enunciado queda:
S = A u B u Φ u D = (-∞,0] u (4/3, 2) u [2,+∞) = (-∞,0] u (4/3, +∞).
Espero haberte ayudado.
Antonius Benedictus
el 8/3/18 -
Alguien me puede ayudar? he hecho una regla de 3 compuesta indirectamente proporcional pero no me da bien...
Un trabajo se ha realizado con 50 obreros que emplearon 15 días trabajando 10 h diarias. Si el trabajo se hiciese con 75 obreros durante 20 días, ¿cuántas horas diarias tendrían que trabajar?
gracias
-
problema 1)
suponer que el semicírculo x2 +y2=a2 , donde a>0 está hecho de alambre con densidad uniforme de 2 gramos por unidad de longitud.
¿Como calculo la masa total del alambre ? y ¿Como calculo su centro de masa?
problema 2)
Como puedo mostrar que la curva C(t)=(t2, 2t-1, √t) con t<0; es una línea de flujo para el campo vectorial F(x,y,z)=(y+1, 2, 1/2z)
Antonio Silvio Palmitano
el 8/3/181)
Planteamos que la semicircunferencia está ubicad en el primero y en el segundo cuadrante (y ≥ 0).
Plantea para la masa de la semicircunferencia (observa que su radio es a y que su centro es el origen de coordenadas):
M = δ*L = 2*(2*π*a/2) = 2*π*a ≅ 2*3,14*a ≅ 6,28*a (en gramos).
Luego, observa que la densidad de masa del alambre es constante, por lo que su masa está distribuida uniformemente en toda la semicircunferencia, y como tienes simetría con respecto al eje OY, tienes que la abscisa del centro de masas de la semicircunferencia queda: xc = 0;
luego, plantea la integral:
I1 = ∫ y*dM = ∫ y*δ*ds = ∫ y*2*dx = 2*∫ x*ds;
luego, puedes plantear el cambio de coordenada:
y = a*senθ, de donde tienes: dx = a*cosθ*dθ, y el elemento de arco de semicircunferencia queda: ds = a*dθ,
luego sustituyes, y la integral queda:
I1 = 2*∫ a*senθ*a*dθ = 2*a2 * ∫ senθ*dθ = 2*a2 * [ -cosθ ], para evaluar con Regla de Barrow entre 0 y π;
luego, evalúas, y queda:
I1 = 2*a2 * ( -(-1) - (-1) ) = 2*a2 * 2 = 4*a2;
luego, planteas la expresión de la ordenada del centro de masas de la semicircunferencia, y queda:
yc = ∫ y*dM / M = I1 / M = reemplazas = 4*a2 / 2*π*a = 2*a/π ≅ 2*a/3,14 ≅ 0,6366*a;
luego, el centro de masas de la semicircunferencia queda expresado: CM( 0 , 2*a/π).
Espero haberte ayudado.
Antonio Silvio Palmitano
el 8/3/182)
Tienes la expresión de la función vectorial de posición para un punto de la trayectoria:
r(t) = < t2 , 2t-1 , √(t) > = < t2 , 2t-1 , t1/2 >, con t > 0;
luego derivas, y la expresión de la función vector tangente para un punto de la trayectoria queda:
r ' (t) = < 2t , 2 , 1/( 2√(t) ) > = < 2t , 2 , t-1/2/2 > (1), con t > 0.
Luego, plantea la expresión del campo vectorial en los puntos de la trayectoria,
para ello sustituyes las componentes de la función de posición ( x = t2, y = 2t-1, z = √(t) ) en la expresión vectorial del campo vectorial ( F(x,y,z) = (< y+1 , 2 , 1/(2z) > ), y queda:
F( r(t) ) = < 2t-1+1 , 2 , 1 / ( 2t1/2 ) > = < 2t , 2 , t-1/2/2 > (2).
Luego, recuerda que el campo vectorial es tangente en todos los puntos de sus líneas de flujo, por lo que tienes que el producto vectorial entre el campo expresado para los puntos de la trayectoria y la función vector tangente para sus puntos debe ser igual al vector nulo:
F( r(t) ) x r ' (t) =
sustituyes las expresiones de las funciones vectoriales señaladas (2) (1), y queda:
= < 2t , 2 , t-1/2/2 > x < 2t , 2 , t-1/2/2 > = < 0 , 0 , 0 >,
porque las dos expresiones vectoriales son iguales.
Espero haberte ayudado.
-
Buenas noches me pueden ayudar?
"Antonio le dice a Pedro: El dinero que tengo es el doble de que tienes tu y pedro contesta: si tu me das 6 euros tendremos los dos la misma cantidad ¿cuanto dinero tiene cada uno?"
Ángel
el 8/3/181er paso)) Traducimos el enunciado de lenguaje ordinario a lenguaje algebraico.
Asignamos el valor en función de x a cada chico:
Antonio le dice a Pedro: El dinero que tengo es el doble de que tienes tu = Antonio tiene el doble de dinero que Pedro
Antonio= 2x euros
Pedro= x euros
Obtenemos la ecuación que nos posibilitará saber el valor de x:
Pedro contesta: si tu me das 6 euros tendremos los dos la misma cantidad = Si le restas a lo que tiene Antonio 6 euros obtienes lo mismo que si le sumas 6 al dinero de Pedro
2x-6=x+6
2º paso)) Deducimos el valor de x de la ecuación del paso 1:
2x-6=x+6
2x-x=6+6
x=12 euros
3er paso)) Obtenemos las soluciones sustituyendo el valor de x obtenido en el paso 2 en los valores de x asignados a cada chico y resulta que:
Antonio= 2*12= 24 euros tiene Antonio.
Pedro= x euros = 12 euros tiene Pedro.
-
Hola, ¿cómo se resolvería el siguiente sistema de 4 ecuaciones con 4 incógnitas?
x = 5 + y
y = 6 + z
(n/x) = (n/y) - 14
(n/y) = (n/z) - 30
He hecho los cálculos con Wiris y la solución me sale → Sol: (n = 1400, x = 25, y = 20, z = 14)
Gracias.
Fran Devesa Peiró
el 8/3/18La forma de abordar este ejercicio depende de hasta dónde hayas llegado, bien con matrices o bien con métodos como el de sustitución (que es el que más utiliza, y visto que no se repiten polinomios es el que te recomendaría). Para el método matricial tienes que poner todas tus incógnitas en un lado de las ecuaciones y asignar a cada columna una incógnita, así pues si tienes 2x+y=5 y x-y=1 tendrías que tu matriz sería de 2x2 de esta forma:
2 1 1 -1 A esta matriz la llamaremos A. Entonces A por el vector de tus incógnitas (una columna con tus incógnitas) (x;y) tendrá que ser igual a tu solución en este ejemplo sería (5;1), llamémosle V. Desde aquí te recomiendo que trates el método de intentar transformar en una matriz diagonal, supongo que tal y como han explicado en clase (he visto que eres de bachiller) que no es más que ir multiplicando y dividiendo las filas e ir restándolas entre ellas con la finalidad que sólo tengas números en tu diagonal, a poder ser que sean unos,pero no es completamente necesario. Acuérdate también, que para hacer este método lo que hacemos es copiar la matriz A e inmediatamente introducir una columna con el vector V. Quedando de este modo:
2 1 5 1 -1 1 De este modo, todo lo que le hagamos a la matriz A también se lo haremos al vector V. Otra recomendación que te puedo dar es empezar a hacer nulos los números de arriba hacia abajo y por debajo de la diagonal de tu matriz, y luego ya encargarte de los de la parte superior de abajo hacia arriba. Así pues, en este ejemplo si multiplicamos toda la segunda fila *2 tenemos que:
2 1 5 2 -2 2 Y si le restamos la primera fila a la segunda obtenemos que:
2 1 5 0 -3 -3 Por lo que ya tenemos como queremos la segunda fila, de todas formas si dividimos entre 3 la segunda fila tendríamos un 1 la diagonal en sentido negativo, que siempre resulta más fácil de operar:
2 1 5 0 -1 -1 A lo que si sumamos a la primera fila la segunda (vamos ahora con la parte superior de la diagonal) tenemos que:
2 0 4 0 -1 -1 Así pues tenemos que: 2x+0y=4 y que 0x-1y=-1, que sí que sabemos resolver fácilmente. x=4/2=2 e y=1.
Si tienes cualquier duda consúltamelo, y si no habéis dado este método te explico otro. No te he querido resolver el sistema porque pienso que puede ser un buen ejercicio para que practiques, ya nos cuentas cómo vas y en qué te has quedado atascado y te ayudamos en lo que sea.
Un saludo.
-
Hola David, yo te quería pedir si podrías hacer algún vídeo sobre supremos e ínfimos
Ángel
el 8/3/18 -
Antonio Silvio Palmitano
el 8/3/186)
Recuerda la expresión de la distancia entre un punto A(p,q) y una recta r cuya ecuación es: ax + by + c = 0: d(r,A) = |ap + bq + c|/√(a2+b2).
Luego, elige un punto de la recta, por ejemplo: A(-5,-5).
Luego, plantea la ecuación de una recta r paralela a la que tienes en tu enunciado: 3x - 4y + c = 0, con c = a determinar.
Luego, planteas la expresión de la distancia entre el punto a y la recta r, tienes en tu enunciado que es igual a 3, y queda la ecuación:
|3(-5) - 4(-5) + c| / √( 32 + (-4)2 ) = 3, resuelves operaciones entre números, haces pasaje de divisor como factor, y queda:
|5 + c| = 15, luego, por definición de valor absoluto, tienes dos opciones:
a)
5 + c = -15, haces pasaje de término, y queda: c = -20, reemplazas en la ecuación de la recta r, y queda: 3x - 4y - 20 = 0;
b)
5 + c = 15, haces pasaje de término, y queda: c = 10, reemplazas en la ecuación de la recta r, y queda: 3x - 4y + 10 = 0.
Por lo tanto, tienes dos soluciones para este problema.
Espero haberte ayudado.
Antonio Silvio Palmitano
el 8/3/18 -
Saca factor común
(y) *(e^2x+3y) + (xy) *( 2e^2x+3y)
Quedaría y * (1+2x)*(e^2x+3y) ?