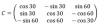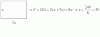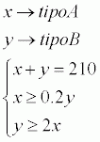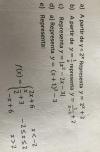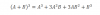-
Las dimensiones de una hoja A4 son 21 cm 29,7 cm. En una práctica de papiroflexia una de ellas ha sido plegada de modo que uno de sus vértices coincide con su opuesto. Calcula el área del polígono resultante.
PERDÓN POR PEDIR LOS EJERCICIOS PERO ME ESTÁN COSTANDO, GRACIIAS
-
buenas
a ver quien me ayuda por favor , lo he intentado pero nada
gracias
sistemas de ecuaciones
Una parcela rectangular tiene un perímetro de 240 m, si mide el triple de largo que de ancho, ¿cuáles son las dimensiones de la parcela?
-
buenas
a ver quien me puede hecha una mano es trigonométrica
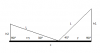
Una escalera de bomberos de 10 m de longitud se ha fijado en un punto de la calzada Si se apoya sobre una de las fachadas forma un ángulo con e! suelo de 45º y si se apoya sobre la otra fachada forma un ángulo de 3QQ. Halla la anchura de la calle. ¿Qué altura se alcanza con dicha escalera sobre cada una de las fachadas?
Antonius Benedictus
el 9/3/18Antonio Silvio Palmitano
el 9/3/18Haz un gráfico, y observa que tienes dos triángulos rectángulos de los que conoces algunas dimensiones (observa que designamos con x al ancho de la calzada, designamos con y a la distancia entre la base de la fachada en la primera situación y el punto de apoyo de la escalera, y observa que la distancia entre el cordón de la acera en la segunda situación y el punto de apoyo de la escalera queda expresada como x - y):
1)
y (longitud de la base),
10 m: (longitud de la hipotenusa, que es igual a la longitud de la escalera),
45° (medida del ángulo interior determinado por la base y la hipotenusa);
luego, puedes plantear la ecuación:
y/10 = cos(45°), multiplicas en ambos miembros por L, y queda:
y = 10*cos(45°) (1),
que es la expresión de la distancia entre el punto de apoyo de la escalera y la base de la primera fachada.
2)
x - y (longitud de la base),
10 m: (longitud de la hipotenusa, que es igual a la longitud de la escalera),
30° (medida del ángulo interior determinado por la base y la hipotenusa);
luego, puedes plantear la ecuación:
(x - y)/10 = cos(30°), multiplicas en ambos miembros por L, y queda:
x - y = 10*cos(30°) (2).
Luego, sustituyes la expresión señalada (1) en la ecuación señalada (2), y queda:
x - 10*cos(45°) = 10*cos(30°), haces pasaje de término, extraes factor común, y queda:
x = 10*( cos(45°) + cos(30°) ), que es la expresión del ancho de la calzada;
Luego, las alturas de los puntos de apoyo de las escaleras sobre las fachadas quedan expresadas:
h1 = 10*sen(45°),
h2 = 10*sen(30°).
Luego, solo queda que hagas los cálculos.
Espero haberte ayudado.
-
En Villacastaños están celebrando una fiesta medieval. Dos comerciantes llegan al puesto aduanero llevando 64 y 20 barriles de cerveza respectivamente. Como no tenían dinero suficiente para pagar los derechos de aduana, el primero de ellos dio 5 barriles y 40 monedas, mientras que el segundo dio 2 barriles, recibiendo 40 monedas como cambio. ¿Cuál era el precio de cada barril y su impuesto aduanero?
ALGUIEN ME PUEDE AYUDAR CON ESTE EJERCICIO ???
-
Buenos días Unicoos:
Tengo que resolver un problema de programación lineal y me estoy haciendo un lío, a ver si me podéis ayudar. Dice asi:
En un contenedor de transporte se pueden guardar 210 ordenadores portátiles. Se pretende llenar de tal forma que finalmente el número de ordenadores de un tipo A sea al menos un 20% del de ordenadores tipo B, y que además el número de ordenadores tipo B sea al menos el doble que los del tipo A. ¿Cuál es el número máximo de ordenadores de tipo A que e puede meter? ¿Y de tipo B ? Tengo problemas para plantear la ecuación y luego las condiciones. entiendo que A+B=210 y que A es mayor o igual que el 20%, que aplicado a 210 sería que A es mayor o igual que 42. Por otro lado B, será menor o igual de 80%, por tanto será menor o igual que 168. Lo que no termino de entender es lo del doble, podría ser que B sea menor o igual que dos A?En fin, que no tengo claro como resolver el problema, a ver si me podéis echar un cable.Muchas gracias de antemano :)
-
Antonius Benedictus
el 9/3/18Antonius Benedictus
el 9/3/18 -
alguien me podria ayudar con el planteamiento del sistema de ecuaciones con este ejercicio de matrices por favor
Una población de 35000 aves vive en tres islas; cada año el 10% de la población de la isla A emigra a la isla B; el 20% de la población de la isla B emigra a la isla C y el 5% de la isla C emigra a la isla A. ¿Cual es el numero de aves de cada isla si la poblacion de cada uno no varia de un año a otro?
Antonio Silvio Palmitano
el 9/3/18Puedes llamar x, y, z a los tamaños iniciales de las poblaciones de aves que hay en las islas A, B, C, respectivamente,
luego, plantea para la cantidad inicial total de aves:
x + y + z = 35000 (1).
Luego, planteas las cantidades finales de aves en cada isla (observa que restamos las cantidades de aves que salen de las islas y sumamos las cantidades de aves que entran)
x - 0,10x + 0,05z, reduces términos semejantes, y queda: 0,90x + 0,05z, para la isla A;
y - 0,20y + 0,10x, reduces términos semejantes, ordenas términos, y queda: 0,10x + 0,80y, para la isla B;
z - 0,05z + 0,20y, reduces términos semejantes, ordenas términos, y queda: 0,20y + 0,95z, para la isla C.
Luego, como los tamaños de las poblaciones de aves que hay en las poblaciones en las islas no varía de un año al otro, puedes igualar las cantidades iniciales y finales para cada isla, y queda:
x = 0,90x + 0,05z, haces pasaje de término, y queda: 0,10x = 0,05z, multiplicas por 10 en ambos miembros, y queda:
x = 0,5z (2);
y = 0,10x + 0,80y, haces pasaje de término, y queda: 0,20y = 0,10x, multiplicas por 100 en ambos miembros, y queda:
2y = x (3);
z = 0,20y + 0,95z, haces pasaje de término, y queda: 0,05z = 0,20y, multiplicas por 20 en ambos miembros, y queda:
z = 4y, (4).
Luego, sustituyes las expresiones señaladas (3) (4) en la ecuación señalada (1), y queda:
2y + y + 4y = 35000, reduces términos semejantes, multiplicas en ambos miembros por 1/7, y queda: y = 5000;
luego, reemplazas el valor remarcado en las ecuaciones señaladas (3) (4), y queda:
10000 = x,
z = 20000;
luego, observa que reemplazas los dos primeros valores remarcados en la ecuación señalada (2), y queda:
10000 = 10000, que es una identidad verdadera, por lo que se verifica que los valores remarcados corresponden a la solución del problema;
y observa, que tal como consigna el colega Antonio, tienes que las cantidades de aves que abandonan las islas son iguales a 1000 individuos en cada isla.
Espero haberte ayudado.