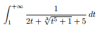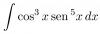-
como se haria este ejercicio 4senx : cosec x
Antonio Silvio Palmitano
el 5/3/18Tienes la expresión trigonométrica:
f(x) = 4*senx / cosecx, expresas a la cosecante en función del seno, expresas al numerador en forma fraccionaria, y queda:
f(x) = (4*senx/1) / (1/senx), resuelves la división entre expresiones fraccionarias, y queda:
f(x) = 4*sen2x.
Espero haberte ayudado.
-
-
Antonio Silvio Palmitano
el 5/3/18Te ayudo con el estudio de la convergencia de la integral.
Observa que la expresión de la función a integrar toma valores positivos, y que su denominador tienes tres términos positivos, en el intervalo [1,+∞),
y que su límite es 0 cuando x tiende a + infinito.
Luego, observa que t toma valores mayores o iguales que 1 en todo el intervalo, y que cualquier potencia con exponente positivo de t toma valores mayores que 1 también.
Luego, plantea comparaciones a partir de la expresión de la función a integrar:
f(x) = 1 / ( 2t + ∛(t5+1) + 5 ) ≤ disminuyes el primero y el tercer término en el denominador, y queda:
≤ 1 / ( 0 + ∛(t5+1) + 0 ) ≤ cancelas términos nulos, disminuyes el argumento de la raíz, y queda.
≤ 1 / ( ∛(t5) ) ≤ expresas como potencia con exponente fraccionario, y queda:
≤ 1 / t5/3 = fc(x), que es la expresión de la función de comparación.
Luego, tienes la integral:
1∫+∞ f(x)*dx ≤ aplicas el Criterio de Comparación ≤ 1∫+∞ fc(x)*dx = 1∫+∞ (1/t5/3)*dt = planteas la integral impropia:
= Lím(b→+∞) 1∫b (1/t5/3)*dt = Lím(b→+∞) [ -(3/2)*(1/t2/3) ] = evalúas con Regla de Barrow:
= Lím(b→+∞) ( -(3/2)*(1/b2/3) + (3/2) ) = resuelves:
= 0 + 3/2 = 3/2;
y por el Criterio de Comparación, tienes que la integral impropia de tu enunciado es convergente.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 5/3/18Vamos con una orientación.
Tienes la expresión de la función a integrar:
f(x) = cos3x*sen5x = cosx*cos2x*sen5x = cosx*(1-sen2x)*sen5x.
Luego, sustituyes, y la integral queda:
I = ∫ cosx*(1-sen2x)*sen5x*dx;
luego, puedes plantear la sustitución (cambio de variable):
w = senx, de donde tienes:
dw = cosx*dx;
luego, sustituyes y la integral queda:
I = ∫ (1-w2)*w5x*dw,
y puedes continuar la tarea.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 5/3/18Plantea las expresiones de los dos términos por separado:
|x-3| =
-x+3 si x < 3 (a)
x-3 si x ≥ 3 (b);
|x+3| =
-x-3 si x < -3 (c)
x+3 si x ≥ -3 (d).
Luego, observa que tienes dos puntos de corte (x = -3 y x = 3), por lo que tienes tres trozos para la expresión de la función de tu enunciado:
f(x) = |x-3|+ |x+3| =
-x+3 + (-x-3) si x < -3 (trozos señalados (a) (c)),
-x+3 + (x+3) si -3 ≤ x < 3 (trozos señalados (a) (d)),
x-3 + (x+3) si x ≥ 3 (trozos señalados (b), (d)),
y observa que los intervalos correspondientes a los trozos señalados (b) (c) no tienen elementos en común;
luego, resuelves expresiones, y queda:
f(x) = |x-3|+ |x+3| =
-2x si x < -3 (A),
6 si -3 ≤ x < 3 (B),
2x si x ≥ 3 (C).
Luego, observa que las expresiones de los tres trozos corresponden a funciones continuas, por lo que solo queda estudiar la continuidad de la función en los dos puntos de corte (x = -3 y x = 3), por medio de la definición:
a)
f(-3) = 6 (observa que pertenece al intervalo del trozo señalado (B);
límites laterales:
Lím(x→-3-) f(x) = Lím(x→-3-) (-2x) = 6,
Lím(x→-3+) f(x) = Lím(x→-3+) (6) = 6,
por lo que el límite de la función existe en este punto de corte, y la función es continua para él, ya que se cumple:
f(-3) = Lím(x→-3) f(x) = 6;
b)
f(3) = 6 (observa que pertenece al intervalo del trozo señalado (C);
límites laterales:
Lím(x→3-) f(x) = Lím(x→3-) (6) = 6,
Lím(x→3+) f(x) = Lím(x→3+) (2x) = 6,
por lo que el límite de la función existe en este punto de corte, y la función es continua para él, ya que se cumple:
f(3) = Lím(x→3) f(x) = 6.
Por todo lo expuesto, puedes concluir que la función es continua en el conjunto de los números reales.
Espero haberte ayudado.
-
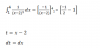 ¿Me podéis ayudar con esta integral? , para resolver la integral he hecho cambio de variable pero el resultado del área me sale negativo , no puede ser negativo ¿ verdad?
¿Me podéis ayudar con esta integral? , para resolver la integral he hecho cambio de variable pero el resultado del área me sale negativo , no puede ser negativo ¿ verdad?Gonzalo
el 5/3/18valor negativo: o la función está por debajo del eje x, o el acumulado lo es (es mayor el área por debajo del eje x en el intervalo); si es área lo que se quiere calcular (y no solo el acumulado) habría que partir el intervalo y restar la parte por debajo.
En este caso en particular es otro el motivo (la primitiva está bien), el problema es que la función no es continua en el intervalo de integración no existe función en x=2. Creo que ese el problema aquí.
Antonio Silvio Palmitano
el 5/3/18Observa que la función a integrar no está definida y su gráfica presenta asíntota vertical en x = 2 que pertenece al intervalo de integración [1,4],
por lo que debes plantar integración impropia.
A =1∫4 ( 1/(x-2)2 )*dx,
aplicas la sustitución (cambio de variable) que propones en tu enunciado (observa que t = -1 cuando x = 1, y que t = 2 cuando x = 4, y queda:
A = -1∫2 ( 1/t2 )*dt,
y observa que la integral presenta una impropiedad para t = 0 que pertenece al intervalo, por lo que debes plantear la suma de dos integrales:
A = -1∫0 ( 1/t2 )*dt + 0∫2 ( 1/t2 )*dt (1).
Luego, resuelves cada integral por separado (observa que has planteado correctamente la expresión de la función primitiva), y tienes:
I1 = Lím(a→0-) -1∫a ( 1/t2 )*dt = Lím(a→0-) [-1/t ] = evalúas con Regla de Barrow = Lím(a→0-) ( -1/a + 1 ) = +∞;
I2 = Lím(b→0+) b∫2 ( 1/t2 )*dt = Lím(b→0+) [-1/t ] = evalúas con Regla de Barrow = Lím(b→0+) ( -1/4 + 1/b ) = +∞;
luego, tienes que los dos términos de la expresión del área señalada (1) tienden a +infinito,
por lo que tienes que el área encerrada bajo la gráfica de la función cuya expresión tienes en tu enunciado es infinita.
Espero haberte ayudado.
-
Hola buenas, no se como resolver el apartado b del siguiente problema (el apartado a, ya lo he hecho): Dados los vectores U=(1, -1,4), V=(2,1,3) y W=(1,0,0). a) Determine si son vectores linealmente dependientes o independientes. b) Calcular la relación que debe haber entre los valores a y b para que el vector (a, 1, b) sea combinación lineal de U y de V.
Muchas gracias.
Antonio Silvio Palmitano
el 5/3/18Puedes plantear la combinación lineal:
k*U + m*V = v, con números reales k, m a determinar.
Reemplazas las expresiones de los vectores en el primer miembro, y del vector de tu enunciado en el segundo miembro, y queda:
k*<1,-1,4> + m*<2,1,3> = <a,1,b>, resuelves los productos en los términos, y queda:
<k,-k,4k> + <2m,m,3m> = <a,1,b>, resuelves la suma vectorial en el primer miembro, y queda:
<k+2m,-k+m,4k+3m> = <a,1,b>;
luego, por igualdad entre vectores, tienes el sistema de tres ecuaciones con dos incógnitas:
k + 2m = a,
-k + m = 1, aquí haces pasaje de término, y queda: m = 1 + k (1),
4k + 3m = b;
luego, sustituyes la expresión señalada (1) en las demás ecuaciones, y queda:
k + 2(1+k) = a,
4k + 3(1+k) = b;
luego, distribuyes en los segundos términos y haces pasajes de términos en ambas ecuaciones, y queda:
3k = a - 2, aquí divides por 3 en todos los términos de la ecuación, y queda: k = a/3 - 2/3 (2),
7k = b - 3;
luego, sustituyes la expresión señalada (2) en la última ecuación, y queda:
7(a/3-2/3) = b - 3, distribuyes el primer miembro, y queda:
7a/3 - 14/3 = b - 3, haces pasaje de término, y queda:
7a/3 - 5/3 = b (3);
luego, sustituyes la expresión remarcada (2) en la ecuación señalada (1), reduces términos semejantes, y queda: m = a/3 + 1/3.
Luego, tienes que existen infinitas soluciones para el vector de tu enunciado, que queda expresado:
v = < a , 1 , b > = sustituyes = < a , 1 , 7a/3-5/3 >, con a ∈ R,
con los escalares: k = a/3 - 2/3 y m = a/3 + 1/3, que permiten expresar a los vectores v como combinaciones lineales de los vectores U y V.
Espero haberte ayudado.
-
Antonio
el 5/3/18y=-2x-1
Calculemos un punto
A(0,-1) hemos sustituido la x por un número cualquiera, en este caso el cero
Calculemos otro punto
B(1,1) hemos sustituido la x por un número cualquiera, en este caso el uno
fíjate que podemos hallar infinitos puntos
Calculemos ahora un vector director de la recta o dicho de otra forma un vector paralelo a la recta
v→= (1,2) hemos restado las dos coordenadas de dos puntos anteriores, es decir: v→= AB→= (1,1) - (0,-1) = (1-0, 1-(-1)) = (1,2)
Calculemos ahora un vector perpendicular a la recta o dicho de otra un vector perpendicular a v→= (1,2)
w→= (2,-1) hemos cambiado el orden a las coordenadas y a uno de ellos el signo (Si quieres saber el porqué pregúntalo)
Es hora de calcular la pendiente de la recta y=-2x-1
m= -2 pues es el número que acompaña a la x cuando la ecuación está en forma explícita
y los puntos de corte
con el eje y solo tenemos que sustituir la x por cero, es decir (0,-1)
y con el eje x solo tenemos que sustituir la y por cero y despejar la x, es decir (-1/2,0)
Y por último ecuación general: 2x+y+1=0 pasando todo al primer miembro e igualando a cero
la paramétrica:
x=1+1λ
y=1+2λ
pues sería x igual a la coordenada x de un punto (1,1) mas la primera coordenada del vector (1,2) por landa e
y sería igual a la coordenada y del punto más la segunda coordenada del vector por landala continua: (x-1)/1=(y-1)/2 sería x menos la coordenada x de un punto (1,1) partido entre la primera coordenada del vector (1,2) igual a y menos la coordenada y del punto partido entre la segunda coordenada del vector
y acabo pasándote un video para la recta normal