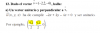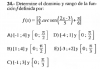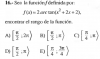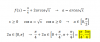-
Antonio Silvio Palmitano
el 6/12/19Tienes la expresión numérica
(∛[2])2 * ∛[2] =
aplicas la propiedad de una multiplicación de potencias con bases iguales, y queda:
= (∛[2])2+1 =
resuelves el exponente, y queda:
= (∛[2])3 =
simplificas el exponente con el índice de la raíz, y queda:
= 2.
Espero haberte ayudado.
-
Jose Ramos
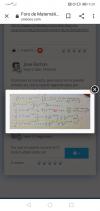
el 6/12/19Toma un plano cuyo vector normal (perpendicular) sea el vector dado (-2,2,-4) que es -2x + 2y +4z +C = 0 (Vale cualquier valor de C, en el ejemplo toma C = 0)
y obtiene el plano -2x + 2y +4z= 0. Ahora advierte que cualquier vector sobre ese plano es perpendicular al vector (-2,2,-4). (Te paso una imagen para que lo veas)
Para tomar un vector sobre ese plano basta con dos puntos y unirlos: Por ejemplo voy a tomar el A(0,0,0) y el B(1,1,0). que me generan el vector AB (1,1,0) que es un vector perpendicular al dado.
Solo me falta hacerlo unitario. Para ello tengo que dividir sus componentes por su módulo que es √2. El vector pedido es (1/√2, 1/√2,0) que racionalizando es (√2/2, √2/2, 0)
-
-
Jose Ramos
el 6/12/19Tú has hecho esto: (2x+1) = 2 (x+1) , lo cual es una incorrecta aplicación de la propiedad distributiva del producto respecto a la suma. No puedes extraer el 2 multiplicando. Otra cosa diferente es que fuese (2x+2) en cuyo caso el 2 multiplica a ambos sumandos y sí se podría extraer factor común.
-
Me pidieron investigar un uso de la función racional pero no sé cómo hacerlo :(
Aparte investigar un problema sobre el seno
He visto diferentes páginas de internet y no se me ocurre que hacer,espero y me puedan ayudar
César
el 6/12/19Mirate esto a ver si es o que buscas
https://prezi.com/1xmzd5k1vcri/funciones-racionales-en-la-vida-cotidiana/
-
-
César
el 6/12/19Antonio Silvio Palmitano
el 6/12/19Vamos con una precisión.
Observa que los puntos que pertenecen al lugar geométrico equidistan de un punto fijo (foco) y de una recta fija (directriz) que es perpendicular al eje polar, por lo que tienes que la representación gráfica del lugar geométrico es una parábola.
Luego, en forma poco ortodoxa puedes plantear la ecuación del lugar geométrico en coordenadas cartesianas, y una vez obtenida la ecuación cartesiana del lugar geométrico, plantear el cambio a coordenadas polares.
Observa que el foco de la parábola se encuentra en el polo, cuya expresión cartesiana es: F(0;0).
Observa que la recta directriz es perpendicular al eje polar y, por lo tanto, también es perpendicular al eje cartesiano OX, por lo que resulta ser paralela al eje cartesiano OY, por lo que su ecuación cartesiana es: x = -3.
Luego, recuerda que el foco pertenece al eje focal de la parábola, que a su vez es perpendicular a la recta directriz, por lo que tienes que el eje focal es el eje OX, y recuerda además que el vértice de la parábola es el punto medio entre el foco y la recta directriz, por lo que tienes que su expresión cartesiana es: V(-3/2;0).
Luego, planteas la expresión del parámetro (recuerda que es igual a la distancia entre el vértice y el foco, en este caso con signo positivo ya que la abscisa del foco es mayor que la abscisa que el vértice), y queda:
c = d(F,V) = √([-3/2 - 0]2 + [0 - 0]2) = √(9/4 + 0) = √(9/4) = 3/2.
Luego, planteas la ecuación cartesiana canónica general de una parábola con eje focal paralelo al eje OX, con vértice V(h;k) y parámetro c, y queda:
(y - k)2 = 4*c*(x - h), reemplazas valores (k = 0, h = -3/2, c = 3/2), y queda:
(y - 0)2 = 4*(3/2)*(x - [-3/2]), resuelves expresiones, y queda:
y2 = 6*(x + 3/2), que es la ecuación cartesiana canónica de la parábola;
luego, distribuyes el segundo miembro, y queda:
y2 = 6*x + 9,
sustituyes las expresiones polares (x = r*cosθ, y = r*senθ), y queda:
(r*senθ)2 = 6*r*cosθ + 9,
distribuyes la potencia en el primer miembro, y queda:
r2*sen2θ = 6*r*cosθ + 9,
restas 6*r*cosθ y restas 9 en ambos miembros, y queda
r2*sen2θ - 6*r*cosθ - 9 = 0,
que es una ecuación polar implícita de la parábola que es gráfica del lugar geométrico al que se refiere tu enunciado.
Espero haberte ayudado.