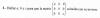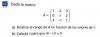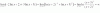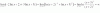-
Jordi García
el 10/2/18Hola, ¿cómo se hace este ejercicio?
Concretamente, ¿cómo elijo las soluciones correctas?
He multiplicado la matriz por sí misma y el resultado lo he igualado con la matriz identidad, pero todas las incógnitas tienen dos soluciones posibles (excepto la b que tiene 3). He probado con la calculadora online de matrices y me salen dos soluciones posibles: a = 1, b = -1, c = 1 y a = 1, b = -1, c = -1. El problema es que no sé cómo escoger las combinaciones correctas sin comprobarlo, supongo que debe de haber alguna manera para saber qué soluciones son las correctas.
Me sale: a = ±1 ; b = 0, -1 ; b = ±1 y c = ±1
Gracias.
-
Pablo
el 9/2/18 -
Jordi García
el 9/2/18 -
Usuario eliminado
el 9/2/18Cogo la primera columna
(-1) ^2 * (1-x) * (-1-x 0 2 + (1/2) * (-1)^3 * ( 1/2 -1 0 + (-1) * (-1)^4 * ( 1/2 -1 0
0 1-x 2 0 1-x 1 -1-x 0 2
2 1 1-x) 2 1 1-x) 2 1 1-x)
(1-x)^4 * (1-x) -4 +4x +1 +x -1/2 * (1-x)^2 -2 -1/2 -4-((1+x)*(1-x)
No se donde esta el error, ya que el resultado no me da lo mismo, me lo puede mirar desde que lo he hecho yo, porfavor.
-
Diego
el 9/2/18 -
Aitor
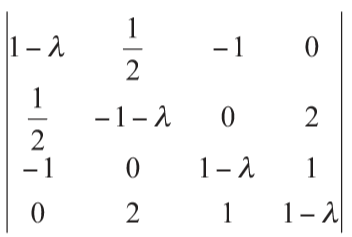
el 9/2/18Hola buenas tardes,
En estadística dice así el ejercicio: de la siguiente tabla de frecuencias (n = ciudades) saque: las ciudades en las que la temperatura máxima haya sido más alta que 42ºC y las que no superaron como temperatura máxima los 10ºC .
A ver si ahora mejor.
Muchas gracias,
-
arieel
el 9/2/18 -
Zanubia Nufuri
el 9/2/18Con el siguiente ejercicio de limite tampoco puedo usar L'hospital:
lim-->x0 sen (3x)/2x
Gracias!!
Antonio Silvio Palmitano
el 9/2/18Recuerda el límite trascendente que has vito en clase:
Lím(u→0) sen(u)/u = 1 (1).
Luego, tienes el límite de tu enunciado, que es indeterminado porque el numerador y el denominador tienden a cero:
L = Lím(x→0) sen(3x)/(2x), extraes el factor constante del denominador, y queda:
L = (1/2) * Lím(x→0) sen(3x)/(x), multiplicas por 3 al numerador y al denominador del argumento, y queda:
L = (1/2) * Lím(x→0) 3*sen(3x)/(3x), extraes el factor constate del numerador, y queda:
L = (3/2) * Lím(x→0) sen(3x)/(3x);
luego, aplicas la sustitución (cambio de variable: u = 3x (observa que u tiende a cero cuando x tiende a cero), y queda:
L = (3/2) * Lím(u→0) sen(u)/u, aplicas el límite trascendente señalado (1), y queda:
L = (3/2)*1 = 3/2.
Observa que puedes verificar la validez del resultado por medio de la Regla de L'Hôpital.
Espero haberte ayudado.
-
Zanubia Nufuri
el 9/2/18Hola!! Gracias a los que me respondieron la consulta, pero estoy tratando de resolver el siguiente limite SIN USAR L'HOSPITAL usando la forma de lim x---> ∞(1+1/x)^x=e pero no logro resolverlo:
limx--->∞ (x/e^x
-
Angel Garcia Curela
el 9/2/18
