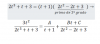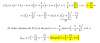-
Angel Garcia Curela
el 8/2/18 -
Juan Ignacio Barranco
el 8/2/18Buenas tardes a todos , me preguntaba si alguien podría ayudarme con la resolución del siguiente límite :
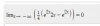
lim [cotg (x)]/[1/x] , usando regla de L'Hospital. Muchas gracias.
x→0+
Antonio Silvio Palmitano
el 8/2/18Observa que el lìmite es indeterminado, ya que el numerador (N) tienede a cero y el denominador (D) tiende a cero.
Luego, derivas el numerador y el denominador por separado, y quedan:
N ' = -1/sen2x,
D ' = -1/x2.
Luego, tienes el lìmite de tu enunciado:
L = Lím(x→0+) cotg(x)/(1/x), aplicas la Regla de L'Hôpital, y queda:
L = Lím(x→0+) (-1/sen2x)/(-1/x2), resuelves la división de expresiones en el argumento, y queda:
L = Lím(x→0+) x2/sen2x (1);
y observa que el numerador (N1) tienede a cero y que el denominador (D1) tiened a cero.
Luego, derivas el numerador y el denominador por separado, y quedan:
N1 ' = 2*x,
D1 ' = 2*senx*cosx.
Luego, tienes el lìmite señalado (1):
L = Lím(x→0+) x2/sen2x,
aplicas la Regla de L'Hôpital, y queda:
L = Lím(x→0+) (2*x)/(2*senx*cosx), simplificas en el argumento, y queda:
L = Lím(x→0+) x/(senx*cosx) (2);
y observa que el numerador (N2) tienede a cero y que el denominador (D2) tiened a cero.
Luego, derivas el numerador y el denominador por separado, y quedan:
N2 ' = 1,
D2 ' = cosx*cosx + senx*(-senx) = cos2x - sen2x.
Luego, tienes el lìmite señalado (2):
L = Lím(x→0+)1/(cos2x - sen2x) = 1,porque el numerador es igual a 1 y el denominador tiende a 1.
Espero haberte ayudado.
-
Usuario eliminado
el 8/2/18 -
Angel Garcia Curela
el 8/2/18
como resuelvo este limite? 
Antonius Benedictus
el 9/2/18
Angel Garcia Curela
el 9/2/18
Antonius Benedictus
el 9/2/18
Angel Garcia Curela
el 9/2/18 -
Javier García
el 8/2/18 -
Angel Garcia Curela
el 8/2/18
que metodo puedo utilizar para realizar esta integral? -
Vivi
el 8/2/18 -
laura
el 8/2/18 -
laura
el 8/2/18 -
andres velasquez
el 8/2/18buenas tardes, hay alguna forma de saber cuantas veces tengo que sumar un numero para llegar a conocer su potencia.
Me explico mejor con un ejemplo:
8 3 = 512 = 8 x 8 x 8 = 64 veces 8ese 64 seria el que yo quisiera averiguar, se que la potencia de ( Be-1 ) daria el numero de veces que debo sumar la base para que me de la siguiente potencia, pero quisiera saber si hay una forma de hallar ese valor sin realizar una pontencia.
