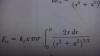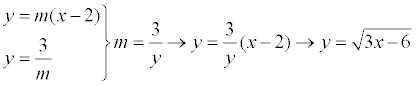-
ALOFRE
el 3/2/18Hola, alguien podría ayudarme con esta integral?
Antonio Silvio Palmitano
el 3/2/18Observa que la variable de integración es r.
Luego, puedes plantear la sustitución (cambio de variable):
w = r2 + x2, de donde tienes:
dw = 2*r*dr, y también tienes los límite de integración:
w1 = w(0) = x2, y w2 = w(R) = R2 + x2.
Luego, sustituyes en la expresión de tu enunciado, y queda:
Ex = ke*x*π*σ * ∫ dw/w3/2 = ke*x*π*σ * ∫ w-3/2*dw;
luego, integras (observa que indicamos con corchetes que debes evaluar con Regla de Barrow), y queda:
Ex = ke*x*π*σ * [ -2*w-1/2 ] = ke*x*π*σ * [ -2/w1/2 ];
luego, evalúas y queda:
Ex = ke*x*π*σ * ( -2/(R2 + x2)1/2 + 2/(x2)1/2 ) = ke*x*π*σ * ( -2/(R2 + x2)1/2 + 2/x );
luego, resuelves el agrupamiento, extraes factor común, ordenas términos, y queda:
Ex = 2*ke*x*π*σ * ( -x + (R2 + x2)1/2 ) / ( x*(R2 + x2)1/2 ).
Espero haberte ayudado.
-
A. Q Torres
el 3/2/18Cómo puedo hallar el vértice de una parábola sin ser por gráfico?
Cómo hallo la tangente?
Antonio Silvio Palmitano
el 3/2/18Planteas la ecuación punto-pendiente de la recta r, y queda:
y = m*(x - 2) (1).
Planteas la ecuación explícita de la recta s, y queda:
y = 3/m (2).
Luego, multiplicas miembro a miembro con las ecuaciones señaladas (1) (2), simplificas en el segundo miembro, y queda:
y2 = 3*(x - 2),
que es una ecuación cartesiana canónica de una parábola cuyo vértice es: V(2,0), su parámetro es: c = 3/4,
y cuyo eje de simetría es la recta paralela al eje OX, cuya ecuación es: y = 0.
Recuerda que la expresión general de la ecuación canónica para esta clase de parábolas es:
(y - k)2 = 4c*(x - h),
en la que el vértice es el punto: V(h,k), c es el parámetro, y el eje de simetría es la recta cuya ecuación cartesiana es: y = k.
Espero haberte ayudado.
-
Usuario eliminado
el 3/2/18 -
A. Q Torres
el 3/2/18 -
Alba Vargas Lozano
el 3/2/18Un problema con método de Gauss: un grupo de personas se reúne para ir de excursión, juntándose en total 20 personas entre hombres, mujeres y niños. Contando hombres y mujeres juntos, su número resulta ser el triple que el número de niños. Además, si hubiera acudido una mujer más, su número igualaría al de hombres. ¿Cuántos hombres mujeres y niños habrá?
-
Usuario eliminado
el 3/2/18 -
Vivi
el 3/2/18 -
Carla Extremera Torras
el 3/2/18 -
Carla Extremera Torras
el 3/2/18 -
Cristina Iglesias
el 3/2/18
Me manda esto un compi ME LO PODRIAIS RESOLVER PARA DARSELO A EL
Gracias es urgente
César
el 3/2/18
Ángel
el 4/2/18a)
f(x)=
-x+1 si x< 0
x2 si x≥ 0
Continuidad
Como tenemos una función lineal y una parábola, entonces son continuas por definición en (-inf,0) y (0,inf) respectivamente.
Veamos en x=0 :
lim(x→0-) -x+1 = 1
lim(x→0+) x2 = 0
Como no coinciden los límites laterales, f(x) no es continua en x=0
Podemos concluir (y confirmar con la representación gráfica), que f(x) es continua en todo el conjunto de los números reales excepto en x=0, que presenta una discontinuidad de salto finito.
