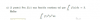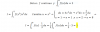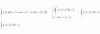-
Teli Marchesani
el 1/2/18
Hola. Necesito ayuda con un ejercicio en el que me piden saber el valor principal de una integral impropia. Yo sé que mi integral diverge, porque lo analicé como corresponde, pero no sé cómo encontrar el valor principal. He visto videos en youtube que usan un teorema de Cauchy cuando la integral va de menos a mas infinito o cuando va de cero al valor donde la función es discontínua, pero qué pasa cuando la discontinuidad está en un c dentro del intervalo? Por ejemplo, tengo que resolver esto:
integral de -2 a 3 de (1/x).1/X es discontínua en c=0, un valor intermedio del intervalo. Si dicha integral diverge (ya lo analicé), cómo encuentro su valor principal? Gracias!!
Antonius Benedictus
el 1/2/18¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
Fátima
el 1/2/18 -
Laura
el 1/2/18Hola unicoos!! Necesito de su ayuda, tengo que hallar la directriz y los números directores de la generatriz de la siguiente superficie cilíndrica: xz+2yz-1=0. Desde ya muchas gracias!
Antonius Benedictus
el 1/2/18¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
Ignasi
el 1/2/18Hola de nuevo, ahí va un ejercicio de semejanza de triángulos:
Tenemos tres palos, de 3 m. , 4 m. y 8 m. de altura. ¿Es posible colocarlos de forma vertical sobre una linea recta en el suelo de modo que sus extremos superiores formen otra linea recta?
¿Es única la solución?
Gracias!
Antonio Silvio Palmitano
el 1/2/18Considera un sistema cartesiano, con eje OX en la recta que pasa por las bases de los palos, y sentido positivo hacia los mismos, y eje OY perpendicular al eje OX, con sentido positivo hacia arriba.
Considera que la recta que pasa por los extremos del rectángulo pasa por el origen, y que su ecuación es: y = m*x.
Luego, puedes llamar a, b, c a las abscisas de los puntos sobre el que se ubican los tres palos,
y observa que las coordenadas de sus extremos son: A(a,3), B(b,4), C(c,8), con a < b < c.
Luego, tienes que los tres puntos pertenecen a la recta cuya ecuación tienes planteada, por lo que reemplazas las coordenadas de los puntos, y tienes el sistema de tres ecuaciones no lineales, con cuatro incógnitas:
3 = m*a, aquí haces pasaje de factor como divisor, y queda: 3/a = m (1),
4 = m*b,
8 = m*c;
luego, sustituyes la expresión señalada (1) en las dos últimas ecuaciones, y queda:
4 = (3/a)*b, aquí multiplicas en ambos miembros por a/3, y queda: (4/3)*a = b (2),
8 = (3/a)*c, aquí multiplicas en ambos miembros por a/3, y queda: (8/3)*a = c (3).
Luego, observa que has podido expresar a las incógnitas m, b. c en función de la incógnita a, que es la abscisa del punto en que se encuentra ubicada la base del primer palo, por lo que tienes infinitas soluciones, que quedan expresadas:
m = 3/a, que es la pendiente de la recta que une los extremos superiores de los palos,
b = (4/3)*a, que es la abscisa que corresponde a la base del segundo palo, en función de la abscisa que corresponde a la base del primero,
c = (8/3)*a, que es la abscisa que corresponde a la base del tercer palo, en función de la abscisa que corresponde a la base del primero,
con a ∈ R y a > 0, que es la abscisa que corresponde a la base del primer palo.
Luego, es cuestión que des valores a la incógnita a, y con cada uno de ellos tendrás distintas ubicaciones para los tres palos.
Espero haberte ayudado.
-
Fátima
el 1/2/18Al resolver este ej. llego a la solución que lamda = 6, para que los limites lateriales sean iguales (Limites =2). Sin embargo f(0) no es igual a 2...Con lo cual a función no seria continua...Pero cuanto vale f(0) entonces? Al sustituir da 0/0, pero entonces la función no estaria definida para x=0, no? Muchas gracias
-
Jose Luis Almansa Rodriguez
el 1/2/18Hola profe david ! Tengo una duda en el video de logaritmos 03, en el tercer ejemplo 3 elevado a 6/2 es igual a 3 elevado a3? O a dos vomo dices?! Me da el resultado log base 3 de 3 =1
Gracias de antemano , y una maravilla este sitio web.
-
Interayuda
el 1/2/18Buenos días UNICOOS, estoy intentando resolver ese ejercicio de GEOMETRÍA EN EL ESPACIO ( adjunto foto) que no me sale, me está liando el hecho que me preguntan LOS PUNTOS DE LA RECTA TALES QUE SU DISTANCIA AL ORIGEN DE COORDENADAS SEA RAIZ CUADRADA DE 14. Lo intenté plantear con la fórmula de DISTANCIA DE UNA RECTA A UN PUNTO (viendo al profesor David en uno de sus vídeos), pero como no tengo las coordenadas del punto (eso me piden, x; y; z). Alguien sabe cómo plantear ese ejercicio.
Gracias a todos por el apoyo.
Saludos.
-
Mathias
el 1/2/18¿Dónde está el error? La respuesta correcta es la (E) pero me da la (C)
-
Josep Near Fuentes
el 1/2/18- saludos, ayuda con este ejercico por favor... x4 -13x2 -kx -90 dividido entre x2 -2x -1 al parecer debe salir como division exacta residuo = 0 (los numero tras la x son exponentes) gracias.
-
A. Q Torres
el 1/2/18Alguien me ayuda a hallar las ecuaciones de las siguientes circunferencias: no me doy cuenta como conseguir los datos... :/
Antonio Silvio Palmitano
el 1/2/18Recuerda que si la circunferencia es tangente al eje OX tienes que su radio es igual al valor absoluto de la ordenada de su centro,
y que la abscisa del punto de tangencia coincide con la abscisa del centro;
y recuerda que si la circunferencia es tangente al eje OY tienes que su radio es igual al valor absoluto de la abscisa de su centro,
y que la ordenada del punto de tangencia coincide con la ordenada del centro.
i)
Como la circunferencia es tangente a los dos ejes coordenados, tienes que su centro queda expresado: C(a,a), con R = │a│:
y su ecuación cartesiana canónica queda expresada:
(x - a)2 + (y - a)2 = a2;
luego, reemplazas las coordenadas del punto P(2,1) que pertenece a la circunferencia, y queda:
(2 - a)2 + (1 - a)2 = a2; desarrollas los binomios elevados al cuadrado, haces pasaje de término, reduces términos semejantes, y queda:
a2 - 6*a + 5 = 0,
que es una ecuación polinómica cuadrática cuyas soluciones son:
a)
a = 5, que al reemplazar en al ecuación de la circunferencia queda:
(x - 5)2 + (y - 5)2 = 25,
que corresponde a una circunferencia con centro C(5,5) y radio 5, que es tangente a los ejes en los puntos: (5,0) y (0,5),
y observa que el punto P(2,1) pertenece a esta circunferencia;
b)
a = 1, que al reemplazar en al ecuación de la circunferencia queda:
(x - 1)2 + (y - 1)2 = 1,
que corresponde a una circunferencia con centro C(1,1) y radio 1, que es tangente a los ejes en los puntos: (1,0) y (0,1),
y observa que el punto P(2,1) pertenece a esta circunferencia.
Espero haberte ayudado.
