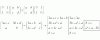Los foros de unicoos se han unificado en beUnicoos. Para dejar preguntas nuevas deberás hacerlo allí, donde además encontrarás el resto de asignaturas y herramientas para ayudarte con tus estudios.
Ir a beUnicoos
Me ayudan con el 45?
Muéstranos tu trabajo y plantéanos dudas muy concretas.
Muéstranos tu trabajo y plantéanos dudas muy concretas.
DEMOSTRAR SI SON CIERTAS LAS SIGUIENTES IGUALDADES:
cotg² α = cosec² α + (cotg α • cos α)²
sen α = sen β (cos α - β) + cos β • sen (α-β)
cotg (α+β) = cotg α • cotg β -1
___________________
cotg α + cotg β
Pon foto del enunciado original.
1)
Aplicas las identidades elementales de la cotangente (cotga = coa/sena) y de la cosecante (coseca = 1/sena), y queda:
(cosa/sena)2 = (1/sena)2 + ( (cosa/sena)*cosa )2;
resuelves cuadrados en el primer miembro y en el primer término del segundo miembro, resuelves el argumento del cuadrado en el segundo término del segundo miembro, y queda:
cos2a/sen2a = 1/sen2a + (cos2a/sena)2;
resuelves potencias en el segundo término del segundo miembro, y queda:
cos2a/sen2a = 1/sen2a + cos4a/sen2a;
extraes denominador común en el segundo miembro, y queda:
cos2a/sen2a = (1 + cos4a)/sen2a;
y tienes que la identidad es Falsa, ya que los denominadores son iguales, pero los numeradores son distintos.
2)
Aplicas las identidades del seno de la resta de dos ángulos (sen(a-b) = sena*cosb - cosa*senb), y del coseno de la resta de dos ángulos (cos(a-b) = cosa*cosb + sena*senb), y queda:
sena = senb*(cosa*cosb + sena*senb) + cosb*(sena*cosb - cosa*senb);
distribuyes en los dos términos del segundo miembro, y queda:
sena = cosa*senb*cosb + sena*sen2b + sena*cos2b - cosa*senb*cosb;
cancelas términos opuestos, extraes factor común, y queda:
sena = sena*(sen2b + cos2b);
aplicas la identidad pitagórica (o fundamental) en el agrupamiento, y queda:
sena = sena*1, resuelves el segundo miembro, y queda:
sena = sena;
y tienes que la identidad es Verdadera.
3)
Aquí es conveniente que trates expresiones por separado:
a)
cotg(a+b) = cos(a+b)/sen(a+b) = aplicas las identidades del coseno y del seno de la suma de dos ángulos:
= (cosa*cosb - sena*senb)/(sena*cosb + cosa*senb);
b)
cotga*cotgb - 1 = (cosa/sena)*(cosb/senb) - 1 = (cosa*cosb)/(sena*senb)- 1 = extraes denominador común:
= (cosa*cosb - sena*senb)/(sena*senb);
c)
cotga + cotgb = cosa/sena + cosb/senb = extraes denominador común:
= (cosa*senb + sena*cosb)/(sena*senb);
luego, sustituyes la expresión señalada (a) en el primer miembro, la expresión señalada (b) en el numerador del segundo miembro, y la expresión señalada (c) en el denominador del segundo miembro, y queda:
(cosa*cosb - sena*senb)/(sena*cosb + cosa*senb) =
= (cosa*cosb - sena*senb)/(sena*senb) / (cosa*senb + sena*cosb)/(sena*senb);
simplificas denominadores en la división del segundo miembro, y queda:
(cosa*cosb - sena*senb)/(sena*cosb + cosa*senb) = (cosa*cosb - sena*senb) / (cosa*senb + sena*cosb);
y tienes que la identidad es Verdadera.
Espero haberte ayudado.
Me ayudan con el 38, no se me ocurre como hacerlo.
Muéstranos tu trabajo y plantéanos dudas muy concretas.
Me ayudan con el 36?
Muéstranos tu trabajo y plantéanos dudas muy concretas.
¿Me ayudarían a darle otra resolución a este ejercicio?
Mira el gráfico se forma un triangulo rectángulo cuyos lados conoces, podras con esos datos, hallar la coordenada que falta del triángulo.
Interesante... ¡Muchas gracias! :)
Hola me gustaría que alguien me ayudase con el ejercicio 3 y 4 Gracias
1º- TE DEJO las operaciones a ti 
Alguien me puede ayudar con estos dos ejercicios de algebra (UNIVERSIDAD) porfavor...
En el primer ejercicio lo que debes hacer es intentar expresar el vector 0 es decir (0,0,0,0) en la base dada por lo que tienes que ir igualando cada 0 del vector a las x, y, z ^ t de los vectores dados:
(0,0,0,0) = a(vector 1)+b(vector 2)...
Y en el caso de que existan a,b,c,d entonces es dependencia lineal.
Y el segundo ejercicio lo que debes hacer es poner las ecuaciones en forma matricula y hacer gauss y finalmente te saldrán los vectores de la base.
No entiendo el porque no es integrable la función a trozos
El conjunto de discontinuidades de la función no tiene medida nula.
No termino de entender lo que quieres decir...
http://webs.um.es/gvb/OCW/OCW-AM-II_files/PDF/Cap10.pdf
derivada de
y= 1/(4x5-3)
y´= (0*(4x5-3) - 1*(20x4))/ (4x5-3)2 = (-20x4)/ (4x5-3)2
