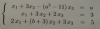logo_unicoos

Foro de preguntas y respuestas de Matemáticas

logo beUnicoos
Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.
Ir a beUnicoos

  • icon

    Sergio
    el 10/1/18

    Como se puede discutir este sistema? 

    reply•thumb_up•0 voto/s•flag
    icon

    César
    el 10/1/18

    https://matrixcalc.org/es/slu.html#analyse-compatibility%28%7B%7B1,3,a%5E2-11,0,a%7D,%7B1,3,2,0,3%7D,%7B2,b%2B3,3,0,5%7D%7D%29


    thumb_up•0 voto/s•flag
  • icon

    Ashley
    el 10/1/18

    Hola, me ayudáis con esta función de límites? Suelo hacer una recta y colocar los valores, pero me lía ver que x no vale 3. Gracias !!!




    reply•thumb_up•0 voto/s•flag
    icon

    Antonio Silvio Palmitano
    el 10/1/18

    Debes aplicar la definición de continuidad de una función en un punto de su dominio.

    1°)

    f(3) = 2k+1 (a determinar).

    2°)

    Lím(x→3) f(x) = Lím(x→3) (5x2-13x-6)/(x2-9) = factorizas:

    = Lím(x→3) 5(x-3)(x+2/5) / (x+3)/(x-3) = simplificas:

    = Lím(x→3) 5(x+2/5)/(x+3) = 17/6.

    3°)

    Planteas:

    f(3) = Lím(x→3) f(x), sustituyes, y queda:

    2k + 1 = 17/6, haces pasaje de término, y queda:

    2k = 11/6, haces pasaje de factor como divisor, y queda:

    k = 11/12.

    Luego, la expresión de la función de tu enunciado queda:

    f(x) = 

    (5x2-13x-6)/(x2-9)                si x ≠ 3

    17/6                                      si x = 3.

    Espero haberte ayudado.


    thumb_up•0 voto/s•flag
  • icon

    David Lucas
    el 10/1/18

    Hola, ¿Podría David hacer un vídeo sobre Posición relativa de tres planos, de 2 de Bachiller? Muchas gracias.

    reply•thumb_up•0 voto/s•flag
  • icon

    Lsslie
    el 10/1/18

    Hola, , pueden ver si tengo este límite bien?  Gracias! !



    reply•thumb_up•0 voto/s•flag
    icon

    Antonio Silvio Palmitano
    el 10/1/18

    Has desarrollado y resuelto el ejercicio en forma correcta.

    thumb_up•0 voto/s•flag
    icon

    Lsslie
    el 10/1/18

    Ese seria el resultado con +infinito, con -infinito solo cambio de signo al resultado??

    thumb_up•0 voto/s•flag
    icon

    Ángel
    el 10/1/18

    Coincide que el valor del límite es 7/2, porque:

    lim(x→ -∞) (7/(1+1)) = 7/2

    lim(x→ ∞) (7/(1+1)) = 7/2

    thumb_up•0 voto/s•flag
  • icon

    Sonia Clavería
    el 10/1/18

    Hola, alguien me puede ayudar con este ejercicio? Gracias


    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 10/1/18


    thumb_up•0 voto/s•flag
    icon

    Ángel
    el 10/1/18

    x2-2x+xy-2x= -4+2x   ---------->   x2+xy-6x+4=0

    3x-3y+xy-4x=xy-2y   ---------->   -x-y=0  ----->  y= -x


    x2+xy-6x+4=0  ----->  x2+x*(-x)-6x+4=0   ------------->  x2-x2-6x+4=0   ----->   6x=4   ----->  x= 2/3

    y= -2/3

    thumb_up•0 voto/s•flag
  • icon

    Ashley
    el 10/1/18

    Buenas, me ayudáis con este ejercicio de límites?  Gracias


    reply•thumb_up•0 voto/s•flag
    icon

    Ángel
    el 10/1/18

    Para que sea continua se ha de cumplir que lim(x->1-) f(x) = f(1) =  lim(x->1+) f(x)


    2*a*1+3=3=12-b*1   -------->  2a+3=3=1-b   ------>  a=0 , b= -2

    thumb_up•0 voto/s•flag
    icon

    Ashley
    el 14/1/18

    El resultado para b no seria 2 ??

    thumb_up•0 voto/s•flag
  • icon

    Lsslie
    el 10/1/18

     Holaa me pueden ayudar con estos dos límites porfaa?? Gracias !!


    reply•thumb_up•0 voto/s•flag
    icon

    Antonio Silvio Palmitano
    el 10/1/18

    Vamos con una orientación.

    r)

    Multiplica al numerador (N) y al denominador (D) por las expresiones "conjugadas" de ambos, y luego distribuye entre factores "conjugados", y quedan:

    N = (√(x+2)-2)(√(x+2)+2)*(√(x+7)+3) = distribuyes entre los dos primeros factores =(x+2-4)*(√(x+7+3) = (x-2)*(V(x+7)+3),

    D = (√(x+7)-3)(√(x+7)+3)*(√(x+2)+2) = distribuyes entre los dos primeros factores = (x+7-9)*(√(x+2)+2) = (x-2)*(√(x+2)+2).

    Luego, sustituyes expresiones, simplificas, y el argumento del límite queda:

    f(x) = (√(x+7)+3) / (√(x+2)+2), y luego puedes calcular el límite.

    s)

    Multiplicas y divides por la expresión "conjugada" del argumento del límite, y el numerador (N) y el denominador (D) quedan:

    N = ( √(x2-2)-√(x2+x-3) )*( √(x2-2)+√(x2+x-3) ) = distribuyes = (x2-2 - (x2+x-3) ) = (x2-2-x2-x+3) = -x+1,

    D = ( √(x2-2)+√(x2+x-3) ).

    Luego, sustituyes expresiones, y el argumento del límite queda:

    g(x) = (-x+1)/( ( √x2-2)+√(x2+x-3) )(x2-2)+√(x2+x-3) ), extraes factores comunes con los mayores exponentes, y queda:

    g(x) = x(-1+1/x) / ( √( x2(1-2/x2) ) + √( x2(1+1/x-3/x2) ) ),

    distribuyes raíces, simplificas índices y exponentes (observa que son pares), y queda:

    g(x) = x(-1+1/x) / ( |x|√(1-2/x2) + |x|√(1+1/x-3/x2) ), extraes factor común en el denominador, y queda:

    g(x) = x(-1+1/x) / |x|( √(1-2/x2) + √(1+1/x-3/x2) ), 

    simplificas (observa que x toma valores positivos, por lo que tienes: x/|x| = x/x = 1), y queda:

    g(x) = (-1+1/x) / ( √(1-2/x2) + √(1+1/x-3/x2) ), y luego puedes calcular el límite.

    Espero haberte ayudado.

    thumb_up•0 voto/s•flag
  • icon

    Thomas
    el 10/1/18

    Muy buenas, ¿Para cuando un vídeo de integración numérica?

    Un saludo

    reply•thumb_up•0 voto/s•flag
  • icon

    Sonia Ramis García
    el 10/1/18

    Tengo muchas dificultades para sacar las Asintotas, los puntos críticos y crecimiento y los puntos de inflexión y concavidad de: xe^1/x. ¿podéis enseñarme como es el ejercicio?

    reply•thumb_up•0 voto/s•flag
  • icon

    Irene Rama Maigler
    el 10/1/18
    flag

    ¿Alguien me podría explicar como calcular los betas de estas matrices? NO SÉ COMO SE PUEDE CALCULAR LA MATRIZ INVERSA SI NO SON CUADRADAS. Solo pongo esa parte del ejercicio porque la duda que tengo es el proceso que hay que seguir para hacer inversa una matriz NO cuadrada. MUCHAS GRACIAS!


    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 10/1/18

    ¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que  lo entiendas.

    Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).

    thumb_up•0 voto/s•flag
    icon

    Rodrigo Ivan Saez
    el 11/1/18

    por lo que alcanzo a entender, lo primero que se hizo fue multiplicar (X1)^t * (X1) , ese producto da como resultado una matriz cuadrada, y a esa se le calculo la inversa

    thumb_up•0 voto/s•flag