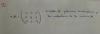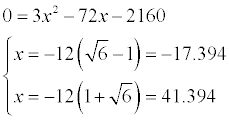Planteamos el determinante:

|A - λ*I| =

(2-λ)       0       0

  0        (4-λ)    3

  0          3    (-4-λ);

resuelves el determinante (puedes desarrollarlo según su primera fila, o con la Regla de Sarrus), igualas a cero, y la ecuación característica queda:

(2-λ)*( (4-λ)*(-4-λ) - 3*3 ) = 0,

resuelves productos en el segundo agrupamiento (observa que tienes cancelaciones), y queda:

(2-λ)*(-16+λ² - 9) = 0,

reduces términos semejantes en el segundo agrupamiento, y queda:

(2-λ)*(λ²-25) = 0,

factorizas el segundo agrupamiento (observa que tienes una resta de cuadrados perfectos), y queda:

(2-λ)*(λ-5)*(λ+5) = 0,

luego, por anulación de un producto, igualas cada factor a cero por separado, despejas, y tienes los autovalores.

λ₁ = 2, λ₂ = 5, λ₃ = -5.

Espero haberte ayudado.

Por favor, sube fotos de los enunciados para que podamos ayudarte.

Recuerda la expresión de la suma de los n primeros elementos de una progresión geométrica:

S_n = a₁*(1-rⁿ)/(1-r), con n ∈ N, n ≥ 1.

Luego, tienes en tu enunciado

S₆ = 9*S₃, sustituyes expresiones, y queda:

a₁*(1-r⁶)/(1-r) = 9*a₁*(1-r³)/(1-r), 

multiplicas en ambos miembros por (1-r/a₁, y queda:

1 - r⁶ = 9*(1 - r³), 

factorizas en el primer miembro (observa que tienes una resta entre cuadrados perfectos), y queda:

(1+r³)*(1-r³) = 9*(1-r³),

haces pasaje de término, y queda:

(1+r³)*(1-r³) - 9*(1-r³) = 0,

extraes factor común, y queda:

(1+r³ - 9)*(1-r³) = 0,

reduces términos semejantes en el primer agrupamiento, y queda:

(r³ - 8)*(1 - r³) = 0.

Luego, por anulación de un producto, tienes dos opciones:

a) 

r³ - 8 = 0, haces pasaje de término, y luego de potencia como raíz, y queda: r = 2,

y para esta progresión tienes:

S₃ = a₁*(1-2³)/(1-2) = a₁*(1-8)/(-1) = a₁*(-7)/(-1) =7*a₁,

S₃ = a₁*(1-2⁶)/(1-2) = a₁*(1-64)/(-1) = a₁*(-63)/(-1) =63*a₁;

b)

1 - r³ = 0, de donde puedes despejar: r = 1,

y observa que en este caso no tienes una progresión geométrica, sino una progresión constante,

por lo que esta razón, r = 1, no corresponde a este ejercicio.

Espero haberte ayudado.

¡Muchas gracias!

¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que  lo entiendas.

Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).

3Q²-72Q -2160= 0       

Q_1,2= (72±√((-72)²-4*3*(-2160)))/(2*3)

Q_1,2= (72±√(5184+25920))/(2*3)   

Q_1,2= (72±√(31104))/(2*3)                 

Q_1,2 ≈ (72±176.36)/(2*3)    

Q₁≈ (72+176.36)/(2*3) ≈     41.3938    

Q₂≈ (72-176.36)/(2*3) ≈  -17.3938

***Parece que tu profe dividió entre 2 en lugar de 2*3 . Es la razón de que se obtenga un resultado de 124.18 en vez de 41.3938, que es el resultado correcto.

Tienes una expresión algebraica fraccionaria,

cuyo numerador es: P(x) = x⁴ - 2x³ + 3x² - x + 3,

y cuyo denominador es: Q(x) = x² - 2x² + 3x = x(x²-2x+3);

luego, efectúas la división, y el cociente queda: C(x) = x, y el resto queda: R(x) = -x + 3.

Luego, puedes estandarizar la expresión de la función a integrar:

f(x) = P(x)/Q(x) = C(x) + R(x)/Q(x), sustituyes expresiones, y queda:

f(x) = x + (-x+3) / x(x²-2x+3) (*).

Luego, observa que el primer término es integrable en forma directa, 

y observa que para integrar el segundo término debes aplicar el Método de las Fracciones Parciales:

(-x+3) / x(x²-2x+3) = a/x + (bx+c)/(x²-2x+3) = ( a(x²-2x+3) + (bx+c)x ) / x(x²-2x+3) (**);

luego, igualas los numeradores remarcados (observa que los denominadores son iguales),

y tienes la igualdad entre polinomios:

a(x²-2x+3) + (bx+c)x = -x+3;

luego, evalúas para tres valores reales (elegimos: x = 0, x = 1 y x = -1), y tienes el sistema de ecuaciones:

3a = 3, aquí haces pasaje de factor como divisor, y queda: a = 1,

2a + b + c = 2,

6a + b - c = 4;

luego, reemplazas el valor remarcado en las dos ecuaciones, haces pasajes de términos, y queda:

b + c = 0, aquí haces pasaje de término, y queda: c = -b (1),

b - c = -2,

sustituyes la expresión señalada (1) en la última ecuación, reduces términos semejantes, haces pasaje de factor como divisor, y queda: b = -1;

luego sustituyes el último valor remarcado en la ecuación señalada (1), y queda: c = 1;

luego, reemplazas en la expresión señalada (**), y el término fraccionario de la expresión de la función a integrar queda:

(-x+3) / x(x²-2x+3) = 1/x + (-x+1)/(x²-2x+3) = 1/x - (x-1)/(x²-2x+3);

luego sustituyes en la expresión estandarizada completa de la función a integrar señalada (*), y queda:

f(x) = x + 1/x - (x-1)/(x²-2x+3) = x + 1/x - (x-1)/( x²-2x+1 + 2 ) = x + 1/x - (x-1)/( (x-1)²+2).

Luego, plantea la integral, a la que puedes separar en tres términos, de los que damos los resultados de los dos primeros, y dejamos expresada la integral del tercero:

I = ∫ f(x)*dx = x²/2 + ln|x| - ∫ ( (x-1)/( (x-1)²+2) )*dx;

luego, plantea la sustitución (cambio de variable) x = w+1,

de donde tienes: dx = dw, y también tienes: x-1 = w (2);

luego, sustituyes en la integral que queda por resolver, y queda:

I = x²/2 + ln|x| - ∫ ( w/(w²+2) )*dw,

luego, multiplicas por (1/2) y por 2 en la integral que queda por resolver, y queda:

I = x²/2 + ln|x| - (1/2)*∫ ( 2w/(w²+2) )*dw;

luego, plantea la sustitución (cambio de variable):

p = w²+2 (3), de donde tienes dp = 2w*dw,

luego, sustituyes en la integral que queda por resolver, y queda:

I = x²/2 + ln|x| - (1/2)*∫ (1/p)*dp;

luego, integras en el último término, y queda:

I = x²/2 + ln|x| - (1/2)*ln|p| + C;

luego, sustituyes la expresión señalada (3), y queda:

I = x²/2 + ln|x| - (1/2)*ln|w²+2| + C;

luego, sustituyes la expresión señalada (2), y queda:

I = x²/2 + ln|x| - (1/2)*ln|(x-1)²+2| + C.

Espero haberte ayudado.

Vamos con una orientación.

Plantea la sustitución: x = 2*senw,

de donde tienes: dx = 2*cosw*dw,

también tienes: √(4-x²) = √(4-4*sen²w) = √( 4*(1-sen²w) ) = √(4*cos²w) = 2*cosw,

y también tienes: x/2 = senw, y luego tienes: arcsen(x/2) = w (1);

luego, sustituyes en la integral de tu enunciado, y queda:

I = ∫ (2*senw)²*(2*cosw)*(2*cosw*dw) = 4*∫ (2*senw)²*(cosw)²*dw =  4*∫ (2*senw*cosw)²*dw;

luego, aplicas la identidad trigonométrica del seno del doble de un ángulo en el argumento de la integral, y queda:

I = 4*∫ ( sen(2w) )²*dw;

luego, aplicas la identidad trigonométrica del cuadrado del seno de un ángulo en función del coseno de su doble, y queda:

I = 4* ∫ ( ( 1-cos(4w) )/2 )*dw = 2*∫ ( 1-cos(4w) )*dw = 2*∫ 1*dw - 2*∫ cos(4w)*dw;

luego, resuelves las integrales, y queda:

I = 2*w - 2*sen(4w)/4 + C = 2*w - (1/2)*sen(4w) + C;

luego, queda que sustituyas la expresión señalada (2), y tienes la expresión de la integral con la variable original.

Espero haberte ayudado.

No, Ylenia.

Pero, si a la izquierda además del 1 me sale un 2, ¿tendría que poner esos 2 números?

El polinomio es    (a+2)(a-1)^2