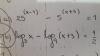¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que  lo entiendas.

Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).

Vamos con una orientación.

Tienes la expresión de la función: f(x,y) = x²y²- 2xy² - x² + 2x, cuyo dominio es R².

Luego, plantea las expresiones de sus derivadas parciales primeras

f_x = 2xy² - 2y² - 2x + 2,

f_y = 2x²y - 4xy² = 2xy(x-2y);

luego, observa que ambas derivadas parciales están definidas en R², por lo que puedes plantear la condición de punto estacionario, y tienes el sistema de ecuaciones:

2xy² - 2y² - 2x + 2 = 0,

2xy(x-2y) = 0;

luego, por anulación de un producto, tienes tres opciones a partir de la segunda ecuación:

a)

x = 0, que al sustituir en la otra expresión queda:

-2y² + 2 = 0, que conduce a: y = ±1,

por lo que tienes dos puntos estacionarios: A₁(0,-1) y A₂(0,1);

b)

y = 0, que al sustituir en la primera ecuación queda:

-2x + 2 = 0, que conduce a: x = 1,

por lo que tienes un punto estacionario: B(1,0);

c)

x = 2y (*), que al sustituir en la primera ecuación queda:

4y³ - 2y² - 4y + 2 = 0, divides por 2 en todos los términos de la ecuación, y queda:

2y³ - y² - 2y + 1 = 0, extraes factor común por grupos de dos términos, y queda:

(2y-1)*(y²-1) = 0, factorizas el segundo agrupamiento, y queda:

(2y-1)*(y+1)*(y-1) = 0, que por anulación de un producto, conduce a tres opciones:

y = 1/2, reemplazas en la ecuación señalada (*) y tienes: x = 1, por lo que tienes el punto estacionario: C₁(1,1/2),

y = -1, reemplazas en la ecuación señalada (*) y tienes: x = -2, por lo que tienes el punto estacionario: C₂(-2,-1),

y = 1, reemplazas en la ecuación señalada (*) y tienes: x = 2, por lo que tienes el punto estacionario: C₃(2,1).

Luego, plantea las expresiones de las derivadas parciales segundas de la función

f_xx = 2y² - 2,

f_xy = 4xy - 4y,

f_yx = 4xy - 4y,

f_yy = 2x² - 8xy.

Luego, queda que evalúes las expresiones de las cuatro derivadas parciales segundas de la función para cada uno de los seis puntos estacionarios, y que plantees para cada uno de ellos el valor del discriminante hessiano, a fin de determinar si se trata de un máximo relativo, un mínimo relativo, o un punto de ensilladura.

Haz el intento de concluir la tarea y, si te resulta necesario, no dudes en volver a consultar.

Espero haberte ayudado.

He visto que falta un 2 en fx , por lo demás creo qie podera servirte

Vamos con una orientacion:

Es muy conveniente que realices gráficos, tanto de R³ ("en 3D"), como de la región de proyección del sólido sobre el plano coordenado OXY.

a)

Dibuja las curvas que delimitan la región de integración (una parábola con eje OY positivo, y otra parábola con eje OX positivo). Luego, plantea el sistema de ecuaciones correspondientes, y verás que las parábolas se cortan en los puntos A(0,0) y B(1,1).

Luego, haz un gráfico, y verás que la región está limitada "por arriba" por la parábola de con eje OX, cuya ecuación explícita es: y = x^1/2, y que está limitada "por debajo" por la parábola con eje OY, cuya ecuación explícita es y = x².

Luego, tienes que la región queda descrita con las inecuaciones dobles:

x² ≤ y ≤ x^1/2

0 ≤ x ≤ 1.

Luego, el volumen queda planteado:

V = ∫∫_R ( (x²+y²) - (0) )*dy*dx = ∫∫_R (x²+y²)*dy*dx = y puedes continuar la tarea.

b)

Observa que la región de proyección del sólido sobre el plano OXY, que es la base del mismo, está limitada por las rectas cuyas ecuaciones son:

x = 0 (eje OY),

y = 0 (eje OX),

x + y = 1 (recta oblicua).

Luego, observa que la región es un triángulo rectángulo en A(0,0), cuyos otros vértices son: B(0,1) y C(1,0).

Luego, observa que la región está limitada "por arriba" por la recta inclinada, cuya ecuación explícita es: y = 1-x, y "por debajo" por el eje OX, cuya ecuación explícita es: y = 0.

Luego, tienes que la región queda descrita con las inecuaciones dobles:

0 ≤ y ≤ 1-x

0 ≤ x ≤ 1.

Luego, el volumen queda planteado:

V = ∫∫_R ( (x²+y²) - (0) )*dy*dx = ∫∫_R (x²+y²)*dy*dx = y puedes continuar la tarea.

Haz el intento de hacer los planteos y resolver los ejercicios, y si te es necesario, no dudes en volver a consultar.

Espero haberte ayudado.

Tienes:

I_n = ∫ ( xⁿ/√(1+x) )*dx = ∫ xⁿ*( 1/√(1+x) )*dx,

y observa que puedes plantear también (sustituyes n-1 en lugar de n):

I_n-1 = ∫ ( x^n-1/√(1+x) )*dx (1).

Luego, plantea el Método de Integración por Partes en la primera integral remarcada:

u = xⁿ, de donde tienes: du = n*x^n-1*dx,

dv =  ( 1/√(1+x) )*dx, de donde tienes: v = 2*√(1+x);

luego, aplicas el método, y queda:

I_n = xⁿ*2*√(1+x) - ∫ 2*√(1+x)*n*x^n-1*dx,

ordenas factores en ambos términos, extraes factores constantes en la integral secundaria, y queda:

I_n = 2*xⁿ*√(1+x) - 2*n*∫ x^n-1*√(1+x)*dx,

sustituyes la expresión señalada (1) en lugar de la integral secundaria, y queda:

I_n = 2*xⁿ*√(1+x) - 2*n*I_n-1.

Espero haberte ayudado.

Hola! gracias, pero creo que no es igual a lo que me piden demostrar.

Además llegas a que:

In = 2*xn*√(1+x) - 2*n*∫ xn-1*√(1+x)*dx

que es distinto a 

2*xn*√(1+x) - 2*n*∫ xn-1 /√(1+x)*dx

Tienes la ecuación vectorial paramétrica del plano, y puede plantear para su vector normal

n = <-1,0,-3> x <-1,-1,0> = <-3,3,1>;

luego, con las coordenadas del punto A(-5,-4,1) puedes plantear la ecuación cartesiana implícita (o general) del plano:

-3*(x+5) + 3*(y+4) + 1*(z-1) = 0, distribuyes, reduces términos semejantes, y queda:

-3x + 3y + z - 4 = 0.

Luego, plantea la ecuación de la distancia entre un punto genérico A(a,b,c) y el plano:

|-3a+3b+c-4|/√( (-3)²+(3)²+(1)² ) = 2*√(19), resuelves el denominador en el primer miembro, y queda:

|-3a+3b+c-4|/√(19) = 2*√(19), haces pasaje de divisor como factor, resuelves el segundo miembro, y queda:

|-3a+3b+c-4| = 38,

que es una ecuación con tres incógnitas, por lo que tienes infinitas soluciones, y cada una de ellas corresponde a un punto cuya distancia al plano es igual a 2*√(19).

Por ejemplo:

si estableceses: a = 0, y b = 0, reemplazas en la ecuación, y queda:

|c-4| = 38, de donde tienes dos opciones, de acuerdo con la definición de valor absoluto:

a₁)

c -  4 = 38, aquí haces pasaje de término, y queda c = 42, y tienes el punto: A₁(0,0,42);

a₂)

c -  4 = -38, aquí haces pasaje de término, y queda c = -34, y tienes el punto: A₂(0,0,-34).

Luego, plantea las ecuaciones de los planos paralelos al plano del enunciado, que pasan por los puntos indicados (observa que su vector normal es n = <-3,3,1>:

Π₁:

-3*(x-0) + 3*(y-0) + 1*(z-42) = 0, distribuyes, cancelas términos nulos, y queda:

-3x + 3y + z - 42 = 0, y observa que todos los puntos de este plano cumplen con la condición del enunciado;

Π₂:

-3*(x-0) + 3*(y-0) + 1*(z+34) = 0, distribuyes, cancelas términos nulos, y queda:

-3x + 3y + z + 34 = 0, y observa que todos los puntos de este plano cumplen con la condición del enunciado.

Espero haberte ayudado.

Por favor, verifica la ecuación vectorial de la recta r (observa que no has consignado signo de igualdad en ella), y envía el enunciado luego, para que podamos ayudarte.

Se trata de un error en la guía, lo tienes perfecto.

Has resuelto el ejercicio correctamente, y deberás consultar con tus docentes a fin de determinar si hay error en el solucionario, o en el enunciado del ejercicio.

Espero haberte ayudado.

¡Agradecido!

Por favor, sube la imagen directamente al foro para que podamos ayudarte.

Comienza por plantear las ecuaciones cartesianas paramétricas de la recta r; para ello, igualas a t a cada uno de los miembros de sus ecuaciones cartesianas simétricas (o continuas), despejas, y queda:

x = 2 + t

y = 1 + kt

z = -1 + 2t,

con t ∈ R.

Luego, observa que el vector director de la recta r queda: u_r = <1,k,2>,

y que el punto A(2,1,-1) pertenece a la recta r.

Luego, observa que el vector director de la recta s queda: u_s = <1,-1,2>,

y que el punto B(1,2,0) pertenece a la recta s.

a)

Observa que si planteas: k = -1 tienes que las rectas tienen el mismo vector director, pero como el punto A no pertenece a la recta s (te dejo la verificación correspondiente), tienes que las rectas son paralelas y, por lo tanto, están incluidas en un mismo plano.

b)

Para el valor remarcado, tienes que las ecuaciones cartesianas de la recta r quedan:

x = 2 + t

y = 1 - t

z = -1 + 2t,

con t ∈ R.

Luego, tienes que el punto B(1,2,0) pertenece al plano que contiene a las rectas, 

y tienes también que el vector: w = BA = <1,-1,-1> pertenece a dicho plano.

Luego, puedes plantear que el producto vectorial entre el vector director de la recta s y el vector w es un vector normal al plano que contiene a las rectas:

n = u_s x w = <1,-1,2> x <1,-1,-1> = <3,3,0>;

luego, con las componentes del vector n y las coordenadas del punto B, puedes plantear la ecuación cartesiana del plano que contiene a las rectas r y s:

3*(x-1) + 3*(y-2) + 0*(z-0) = 0, 

cancelas el término nulo, distribuyes, reduces términos semejantes, y queda:

3x + 3y - 9 = 0,

haces pasaje de término, divides en todos los términos de la ecuación por 3, y qeuda:

x + y = 3, 

que es la ecuación del plano que contiene a las dos rectas del enunciado.

c)

Observa que como la recta r y la recta s son paralelas, tienes infinitas rectas que son perpendiculares a ambas, y todas están incluidas en el plano cuya ecuación hemos determinado.

Luego, a fin de determinar el vector director, puedes considerar que es igual al producto vectorial entre el vector normal al plano que contiene a todas las rectas (n), y al vector director de las rectas paralelas (u_s = u_r), por lo que tienes:

u_p = n x u_s = <3,3 0> x <1,-1,2> = <6,-6,-6>,

que es un vector director de todas las rectas perpendiculares a la recta r y a la recta s,

por ejemplos:

c₁)

si el punto A pertenece a la recta, ésta tiene ecuaciones cartesianas paramétricas:

x = 2 + 6m

y = 1 - 6m

z = -1 - 6m,

con m ∈ R;

c₂)

si el punto B pertenece a la recta, ésta tiene ecuaciones cartesianas paramétricas:

x = 1 + 6d

y = 2 - 6d

z = 0 - 6d,

con d ∈ R;

c₃)

para el caso general, en que la recta perpendicular a las rectas r y s pasa por cualquier punto genérico del plano que las contiene, observa que el punto genérico del plano queda expresado G(g,3-g,h), con g ∈ R y h ∈ R, y las ecuaciones cartesianas paramétricas de la recta perpendicular quedan planteadas:

x = g + 6q

y = 3-g - 6q

z = h - 6q,

con q ∈ R, y también g ∈ R y h ∈ R.

Espero haberte ayudado.

Vamos con una orientación.

Comienza por tratar cada término por separado, en ambas ecuaciones.

a)

25^x-1 = 25^x/25¹ = (5²)^x/25 = (1/25)*(5^x)²,

5^x+3 = 5^x*5³ = 5^x*125 = 125*5^x;

luego, aplicas la sustitución (cambio de incógnita):

5^x = w (observa que w toma valores estrictamente positivos), sustituyes, y queda:

(1/25)*w² - 125*w = 1;

multiplicas por 25 en todos los términos de la ecuación, haces pasaje de término, y queda:

w² - 3125*w - 25 = 0,

que es una ecuación polinómica cuadrática que puedes resolver como has visto en clase.

b)

Considera el segundo término del primer miembro:

log₉(x+3) = a (1), compones en ambos miembros con la función inversa del logaritmo en base 9, y queda:

x + 3 = 9^a, escribes a 9 como potencia en base 3, y queda:

x + 3 = (3²)^a, resuelves las potencias en el segundo miembro, y queda:

x + 3 = 3^2*a. compones en ambos miembros con la función logarítmica en base 3, y queda:

log₃(x+3) = 2*a, multiplicas por 1/2 en ambos miembros, y queda:

(1/2)*log₃(x+3) = a, sustituyes la expresión señalada (1) en el segundo miembro, y queda:

log₉(x+3) = (1/2)*log₃(x+3);

luego, sustituyes en la ecuación de tu enunciado, y queda:

log₃(x) - (1/2)*log₃(x+3) = 1/2, multiplicas por 2 en todos los términos de la ecuación, y queda:

2*log₃(x) - log₃(x+3) = 1, aplicas la propiedad del logaritmo de una potencia en el primer miembro, y queda:

log₃(x²) - log₃(x+3) = 1, aplicas la propiedad del logaritmo de una división en el primer miembro, y queda:

log₃( x²/(x+3) ) = 1, compones en ambos miembros con la función inversa del logaritmo en base 3, y queda:

x²/(x+3) = 3¹, resuelves el segundo miembro, haces pasaje de divisor como factor, y queda

x² = 3*(x + 3), distribuyes en el segundo miembro, haces pasajes de términos, y queda:

x² - 3*x - 9 = 0,

que es una ecuación polinómica cuadrática que puedes resolver como has visto en clase.

Espero haberte ayudado.

Vamos con una precisión.

Colega Ángel: el paso que has consignado:

" Eliminamos la base común:

52(x-1)  - 5(x+3) = 50  "

no es correcto, porque solo se pueden cancelar bases si en el primer miembro hubiese una multiplicación, o una división, de potencias con bases iguales, en este caso de base cinco.

Vamos con un contraejemplo:

5 - 1 = 4,

expresamos cada término como potencia de base 5, y queda:

5¹ + 5⁰ = 5^log₅(4),

luego, si cancelamos bases, queda:

1 + 0 = log₅(4),

resolvemos el primer miembro:

1 = log₅(4),

expresamos el primer miembro como un logaritmo en base 5, y queda:

log₅(5) = log₅(4),

componemos en ambos miembros con la función inversa del logaritmo en base 5, y queda:

5 = 4,

que es una identidad Falsa.

Gracias Antonio por la corrección, quise ver por inercia un producto en lugar de una diferencia :D

Agradezco tanta explicacion...he intentado hacerlo de otra forma.

..cual seria el resultado de ambas ecuaciones???

a)

Tienes planteada la sustitución: w = 5^x (1),

y tienes la ecuación:

w2 - 3125*w - 25 = 0, 

cuyas soluciones quedan expresadas:

w = ( 3125 ± √( (-3125)²-4*1*(-25) ) )/2 = ( 3125 ± √(9765725) )/2,

cuyos valores aproximados, son:

w₁ ≅ -0,07999979520, que no tiene sentido para este problema (recuerda que w toma valores estrictamente positivos);

w₂ ≅ 3125,007999979520, que si tiene sentido para este problema,

y solo queda que reemplaces el valor en la ecuación señalada (1), apliques logaritmos, y tendrás la solución de la ecuación de tu enunciado.

b)

Tienes la ecuación:

x2 - 3*x - 9 = 0, cuyas soluciones quedan expresadas:

x = ( 3 ± √( (-3)²-4*1*(-9) ) )/2 = ( 3 ± √(39) )/2,

cuyos valores aproximados, son:

x₁ ≅ -1,622,

que no tiene sentido para este problema (observa que el argumento en el primer término de la ecuación de tu enunciado debe ser estrictamente positivo);

x₂ ≅ 4,622, que si tiene sentido para este problema,

Espero haberte ayudado.

El resultado del ejercicio a me dio x=5....pero al reemplazarlo ..no se cumple la igualdad del enunciado...es correcto???

w2 ≅ 3125,007999979520 = 5x   ∴  x= ln(3125,007999979520)/ln(5)

Cristina, observa que la x no es exactamente 5

x= ln(3125,007999979520) ÷ ln(5) =      8.047192122÷ 1.609437912=     5.000001592

La reemplazamos:

25^{5.000001592-1} - 5^{5.000001592+3} = 1

25^4.000001592 - 5^8.000001592 = 1

390627.0017 -390626.0017  = 1

1=1                                                                                                                                                                                                                                                                                                               

Concluimos que la respuesta válida para el ejercicio a) es x= 5.000001592