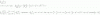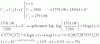-
Tengo el siguiente sistema de ecuaciones lineales que depende de los parámetros a y b. Me piden discutir en función de esos parámetros y resolver el sistema para a=0 y b=3
x-y+5z=2
3x-3y+(4a+1)=3
-3x+(a+4)y-7z=b
-x+(6x+4)y+(a-8)z=1+2b
¿Alguien puede ayudarme? Muchas gracias.
Antonius Benedictus
el 23/12/17Ylenia Montes
el 23/12/17Antonius Benedictus
el 23/12/17Ylenia Montes
el 23/12/17Antonius Benedictus
el 23/12/17Ylenia Montes
el 23/12/17 -
JUAN AMPIE
el 23/12/17 -
Hola, muy buenas.
En un ejercicio me piden que halle algunas superficies de nivel de 2x-3y+4z.
¿Cómo debería proseguir?
Antonius Benedictus
el 23/12/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
Antonio Silvio Palmitano
el 24/12/17Tienes la expresión de una función de tres variables, cuyo dominio es D = R3:
f(x,y,z) = 2x - 3y + 4z.
Luego, plantea la ecuación general de las superficies de nivel:
f(x,y,z) = k, con k ∈ R;
luego, sustituyes la expresión de la función en el primer miembro, y queda:
2x - 3y + 4z = k, con k ∈ R,
que es una ecuación cartesiana implícita de una familia de planos paralelos, cuyo vector normal es: n = <2,-3,4>.
Luego, solo tienes que proponer valores de la constante k, y tendrás algunos planos de la familia, por ejemplo:
2x . 3y + 4z = 0 (para k = 0),
2c - 3y + 4z = 1 (para k = 1),
etcétera.
Espero haberte ayudado.
-
Alguien me podría explicar como despejar la incógnita "i" en esta ecuación:
100000 = 2000/(1+i) + 107000/(1+i)^2
César
el 23/12/17Antonio Silvio Palmitano
el 25/12/17Puedes plantear la sustitución (cambio de incógnita):
1 + i = x (1),
luego sustituyes, y la ecuación queda:
100000 = 2000/x + 107000/x2,
multiplicas en todos los términos por x2 (observa que x debe ser distinto de cero), y queda:
100000*x2 = 2000*x + 107000,
divides en todos los términos de la ecuación por 1000, y queda:
100*x2 = 2*x + 107,
haces pasajes de términos, y queda:
100*x2 - 2*x - 107 = 0,
que es una ecuación polinómica cuadrática, cuyas soluciones son:
a)
x ≅ ( 2 - 206,891)/200 ≅ -1,024,
luego, reemplazas en la ecuación señalada (1), y queda:
1 + i ≅ -1,024,
haces pasaje de término, y queda:
i ≅ -2,024;
b)
x ≅ ( 2 + 206,891)/200 ≅ 1,044,
luego, reemplazas en la ecuación señalada (1), y queda:
1 + i ≅ 1,044,
haces pasaje de término, y queda:
i ≅ 0,044.
Luego, tienes las dos soluciones de la ecuación de tu enunciado, y tendrás que determina si las dos son útiles, o solo una de ellas, o ninguna de las dos, si se trata de la resolución de un problema de aplicación.
Espero haberte ayudado.
-
hola buenas tardes porfavor necesito ayuda en ecuaciones bicuadradas y ecuaciones racionales que no se como se hacen por ejemplo esta:
x4 -25x2 mas 144 igual a 0
GRACIAS UNICOOS
JUAN AMPIE
el 23/12/17Antonio Silvio Palmitano
el 23/12/17Plantea la sustitución (cambio de incógnita):
x2 = w (1), de donde tienes: x4 = (x2)2 = w2 (observa que w toma valores positivos), luego sustituyes y la ecuación queda:
w2 - 25*w + 144 = 0, que es una ecuación polinómica cuadrática cuyas soluciones son:
a)
w = 9, luego sustituyes en la ecuación señalada (1) y queda:
x2 = 9, haces pasaje de potencia como raíz y tienes dos opciones:
x = - 3 o x = 3;
b)
w = 16, luego sustituyes en la ecuación señalada (1) y queda:
x2 = 16, haces pasaje de potencia como raíz y tienes dos opciones:
x = - 4 o x = 4.
Espero haberte ayudado.
-
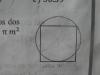
En la figura dos de los vertices del cuadrado estan sobre el circulo y los otros dos vertices estan sobre una tangente al circulo. Si el circulo tiene un area de 25 π m^2 entonces el area del cuadrado, en m^2 es:
a)8 b)64 c)16 d)25 e)50
Antonio Silvio Palmitano
el 23/12/17Plantea la expresión del área para el círculo: π*R2 = Ac, y de ahí puedes despejar para su radio: R = √(A/π) = √(25π/π) = √(25) = 5 m.
Luego, plantea un sistema de coordenadas OXY usual con origen de coordenadas en el centro del círculo, y tienes que:
x2 + y2 = 25 (1) es la ecuación de la circunferencia borde del círculo,
y = -5 (2) es la ecuación de la recta que contiene al lado horizontal inferior del cuadrado,
y = h (3) es la ecuación de la recta que contiene al lado horizontal superior del cuadrado (observa que h es la distancia entre dicho lado y el centro del círculo).
Luego, plantea la intersección del lado superior con la circunferencia, para ello sustituyes la expresión señalada (3) en la ecuación señalada (1), y queda:
x2 + h2 = 25, haces pasaje de término, y queda:
x2 = 25 - h2, haces pasaje de potencia como raíz, y tienes dos opciones:
x = -√(25 - h2), que es la abscisa del vértice superior izquierdo del cuadrado, que queda expresado: A(-√(25 - h2) , h);
x = √(25 - h2), que es la abscisa del vértice superior derecho del cuadrado, que queda expresado: B(√(25 - h2) , h);
luego, plantea la expresión de la distancia entre los dos vértices, desarrollas (te dejo la tarea), y tienes para la longitud del lado horizontal superior del cuadrado:
L = d(A,B), sustituyes la expresión del segundo miembro, y queda:
L = 2*√(25 - h2), elevas al cuadrado en ambos miembros, distribuyes la potencia y simplificas en el segundo miembro, y queda:
L2 = 4*(25 - h2) (4).
Luego, plantea la ecuación de la recta paralela al eje OY que pasa por el vértice superior derecho:
x = √(25 - h2) (5);
luego, plantea su intersección con el lado horizontal inferior cuya ecuación está señalada (2), y con la expresión señalada (5) tienes las coordenadas del punto:
C(√(25 - h2) , -5) que es el vértice inferior derecho del cuadrado.
Luego, plantea que la longitud de la diagonal del cuadrado es igual a la distancia que separa a los vértices A y A:
D = d(C,A), elevas al cuadrado en ambos miembros, y queda:
D2 = dC,A)2, sustituyes la expresión del cuadrado de la distancia entre los puntos A y C en el segundo miembro, y queda:
D2 = ( 2*√(25 - h2) )2 + ( h - (-5) )2, distribuyes la potencia en el primer término, resuelves signos en el argumento de la potencia en el segundo término, y queda:
D2 = 4*(25 - h2) + (h+5)2 (6).
Luego, plantea la relación entre el cuadrado de la longitud de la diagonal de un cuadrado y el cuadrado de la longitud de su lado:
D2 = 2*L2, sustituyes las expresiones señaladas (6) (4), y queda:
4*(25 - h2) + (h+5)2 = 8*(25 - h2), distribuyes y desarrollas en todos lso términos, y queda:
100 - 4*h2 + h2 + 10*h + 25 = 200 - 8*h2, haces pasajes de términos, reduces términos semejantes, ordenas términos, y queda:
5*h2 + 10*h - 75 = 0, divides en todos los términos de la ecuación por 5, y queda:
h2 + 2h - 15 = 0, que es una ecuación polinómica cuadrática cuyas soluciones son:
a)
h = -5, que no tiene sentido para este problema (recuerda que h expresa la distancia entre el lado horizontal superior del cuadrado y el centro del círculo);
b)
h = 3 m, que es la distancia entre el lado horizontal del cuadrado y el centro del círculo.
Luego, reemplazas el valor remarcado en la ecuación señalada (4), y queda:
L2 = 4*(25-32), resuelves el segundo miembro, y queda:
L2 = 64, haces pasaje de potencia como raíz, y queda:
L = 8 m, que es la longitud del lado del cuadrado.
Luego, plantea la expresión del área del cuadrado en función de su lado:
Ak = L2, luego reemplazas, resuelves, y queda:
Ak = 64 m2.
Espero haberte ayudado.
-
Se lanza una piedra, siendo su trayectoria una parábola. La máxima altura que alcanza la piedra es 8mts y cae 32 mts mas allá del punto en que se lanzó la piedra. Hallar la altura que alcanzo la piedra 24 mts más allá del punto en que fue lanzada.
Antonio Silvio Palmitano
el 23/12/17Establece un sistema de referencia con origen en el punto de lanzamiento de la piedra, con eje OX paralelo al suelo con sentido positivo acorde al movimiento, y eje OY vertical con sentido positivo hacia arriba, y considera instante inicial ti = 0 al que corresponde al lanzamiento del proyectil.
Luego, recuerda las ecuaciones de posición y de velocidad de Movimiento Parabólico (observa que la posición inicial es: xi = 0, yi = 0, y que llamamos vi al módulo de la velocidad inicial y α al ángulo de lanzamiento):
x = vi*cosα*t
y = vi*senα*t - (1/2)*g*t2,
vx = vi*cosα,
vy= vi*senα - g*t.
Luego, recuerda las expresiones de la altura máxima y del alcance:
h = vi2*sen2α/(2*g) (1)
A = vi2*sen(2α)/g, aquí aplicas la identidad del seno del doble de un ángulo, y queda:
A = 2*vi2*senα*cosα/g (2)
luego divides miembro a miembro entre las ecuaciones señaladas (1) (2), y queda:
h/A = senα/(4*cosα),
luego aplicas la identidad de la tangente en función del seno y del coseno, y queda:
h/A = tanα/4, haces pasaje de divisor como factor, y queda:
4*h/A = tanα, reemplazas los valores que tienes en tu enunciado (h = 8 m, A = 32 m), y queda:
1 = tanα, compones en ambos miembros de la ecuación con la función inversa de la tangente, y queda:
45° = α, que es la medida del ángulo de lanzamiento del proyectil.
Luego, reemplazas en la ecuación señalada (2), y queda:
32 = 2*vi2*sen(45°)*cos(45°)/g, resuelves factores numéricos (observa que consideramos: g = 10 m/s2), y queda:
32 = vi2/10, haces pasaje de divisor como factor, y queda:
320 = vi2, haces pasaje de potencia como raíz, y queda:
17,889 m/s ≅ vi, que es el módulo de la velocidad inicial del proyectil.
Luego, reemplazas valores en las ecuaciones de posición, y quedan:
x = 17,889*cos(45°)*t,
y = 17,889*sen(45°)*t - 5*t2;
luego, reemplazas el valor de la posición horizontal alcanzada por el proyectil que tienes en el enunciado (x = 24 m), y queda:
24 = 17,889*cos(45°)*t, aquí haces pasajes de factores como divisores, y queda: 1,897 s ≅ t, que es el instante correspondiente,
y = 17,889*sen(45°)*t - 5*t2;
luego reemplazas en la ecuación de altura, y queda:
y ≅ 6,003 m, que es la altura correspondiente.
Espero haberte ayudado.
-
Este problema mr trae de cabeza: Determinar el interes anual a que debe invertirse 1500€ para que en 6 años se obtenga un capital de 1791.08. Gracias
Antonio Silvio Palmitano
el 23/12/17Tienes el capital inicial: C = 1500 euros, con periodo de capitalización de un año, y tienes que que la cantidad de periodos de capitalización es: n = 6.
Luego, puedes llamar i a la razón entre el interés obtenido y el capital invertido al inicio de cada año.
Luego, al final del primer año tienes el capital final:
C1 = C*(1 + i) = C*(1 + i)1.
Luego, al final del segundo año tienes el capital final:
C2 = C1*(1 + i) = C*(1 + i)1*(1 + i) = C*(1 + i)2.
Luego, al final del tercer año tienes el capital final:
C3 = C2*(1 + i) = C*(1 + i)2*(1 + i) = C*(1 + i)3.
Luego, puedes inferir que el capital final al concluir el año número n queda expresado:
Cn = C*(1 + i)n.
Luego, reemplazas el valor del capital al final del sexto año y el valor del capital inicial, y queda:
1791,08 = 1500*(1 + i)6, haces pasaje de potencia como raíz, y queda:
1,194 ≅ (1 + i)6, haces pasaje de potencia como raíz, y queda:
1,030 ≅ 1 + i, haces pasaje de término, y queda:
0,030 ≅ i, que es la razón entre el capital final y el capital al inicio de cada año,
luego multiplicas por 100, y queda:
3,0 % ≅ r, que es la tasa de interés porcentual que ofrece la entidad financiera a sus inversores.
Espero haberte ayudado.
-
Buenos días, podeis ayudarme,
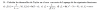 es que no me entero de como hacer el resto de lagrange, se que hay un video, ya lo he visto, pero sigo sin enterarme de como hacerlo, se que primero derivas, pero cuantas veces es necesario hacerlo, porque en el video pone lo del error, pero no se cuantas veces se necesita hacerlo, y tampoco se como sacar la relacion del polinomio. Siento molestarles, un saludo y gracias. :)
es que no me entero de como hacer el resto de lagrange, se que hay un video, ya lo he visto, pero sigo sin enterarme de como hacerlo, se que primero derivas, pero cuantas veces es necesario hacerlo, porque en el video pone lo del error, pero no se cuantas veces se necesita hacerlo, y tampoco se como sacar la relacion del polinomio. Siento molestarles, un saludo y gracias. :)César
el 23/12/17Antonio Silvio Palmitano
el 23/12/17Debes plantear las expresiones de las funciones derivadas hasta encontrar, si es posible, su expresión general.
Te ayudo con el primer ejercicio:
f(0)(x) = 3/(3-x) = 3*(3-x)-1 = 3*0!*(3-x)-1,que evaluada en el centro de desarrollo queda: f(0)(0) = 0! = 0!/1 = 0!/30;
f(1)(x) = 3*(3-x)-2 = 3*1!*(3-x)-2, que evaluada en el centro de desarrollo queda: f(1)(0) = 1!/3 = 1!/31;
f(2)(x) = 3*2*(3-x)-3 = 3*2!*(3-x)-3, que evaluada en el centro de desarrollo queda: f(2)(0) = 2!/9 = 1!/32;
f(3)(x) = 3*2!*3*(3-x)-4 = 3*3!*(3-x)-4, que evaluada en el centro de desarrollo queda: f(3)(0) = 3!/27 = 3!/33;
f(4)(x) = 3*3!*4*(3-x)-5 = 3*4!*(3-x)-5, que evaluada en el centro de desarrollo queda: f(4)(0) = 4!/81 = 4!/34;luego, puedes inferir la expresión para la derivada general:f(k)(x) = 3*k!*(3-x)-(k+1), que evaluada en el centro de desarrollo queda: f(k)(0) = 3*k!/3k+1 = k!/3k.Luego, observa que la última derivada que necesitas para plantear la expresión del polinomio queda:f(n)(x) = 3*n!*(3-x)-(n+1), que evaluada en el centro de desarrollo queda: f(n)(0) = 3*n!/3n+1 = n!/3n.Luego, plantea la siguiente derivada, que es la que debes emplear para la expresión del resto:f(n+1)(x) = 3*(n+1)!*(3-x)-(n+2), que evaluada en valor genérico z queda: f(n+1)(z) = 3*(n+1)!*(3-z)-(n+2) = 3*(n+1)!/(3-z)(n+2), con z comprendido entre 0 y x.Luego, la expresión del polinomio de Taylor asociado a la función, con centro de desarrollo c = 0, queda:Pn(x) = ∑(k=0,n) [f(k)(0)/k!]*(x-0)k,sustituyes la expresión general de las funciones derivadas, simplificas, y queda:Pn(x) = ∑(k=0,n) [1/3k]*xk,;luego, plantea la expresión del resto:Rn(x) = [f(n+1)(z)/(n+1)!]*(x-0)n+1= [3/(3-z)n+2]*xn+1, con z comprendido entre 0 y x.
Espero haberte ayudado.