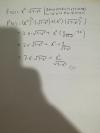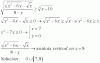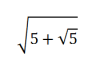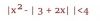-
Antonio Silvio Palmitano
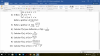
el 23/12/17Observa el triángulo rectángulo NMS:
el cateto opuesto al ángulo θ es NM, cuya medida es|NM| = 5, y el cateto adyacente es MS, cuya medida queda expresada: |MS|;
luego, la expresión de la tangente del ángulo indicado queda:
tanθ = |NM|/|MS|, reemplazas el valor conocido en el numerador, y queda:
tanθ = 5 /|MS| (1).
Observa el triángulo rectángulo YMS:
el cateto opuesto al ángulo θ es MS, cuya medida queda expresada:|MS|, y el cateto adyacente es YM, cuya medida es: |YM| = |YN| + |NM| = 4 + 5 = 9;
luego, la expresión de la tangente del ángulo indicado queda:
tanθ = |MS|/|YM|, reemplazas el valor conocido en el denominador, y queda:
tanθ = |MS| / 9 (2).
Luego, igualas las expresiones señaladas (2) (1), y queda:
|MS| / 9 = 5 /|MS|, haces pasajes de divisores como factores, y queda:
|MS|2 = 45, haces pasaje de potencia como raíz, y queda:
|MS| = √(45) = √(9*5) = √(9)*√(5) = 3*√(5) (3).
Luego, reemplazas el valor señalado (3) en la ecuación señalada (2), y queda:
tanθ = 3*√(5) / 9 = √(5) / 3.
Luego, a modo de verificación, reemplazas el valor señalado (3) y el valor remarcado en la ecuación señalada (1), y queda:
√(5) / 3 = 5 / ( 3*√(5) ), multiplicas al numerador y al denominador del primer miembro por √(5), y queda:
( √(5) )2 / ( 3*√(5) ) = 5 / ( 3*√(5) ), simplificas en el numerador del primer miembro, y queda:
5 / ( 3*√(5) ) = 5 / ( 3*√(5) ), que es una identidad verdadera, por lo que se verifica que el valor remarcado es la respuesta correcta,
que corresponde a la opción señalada (d).
Espero haberte ayudado.
Carla Alexandra Olivas Guerrero
el 23/12/17 -
hola quisiera que me ayude con la derivada de ln(x)/e^x
Antonio Silvio Palmitano
el 22/12/17Tienes la expresión de la función, cuya forma es:
f(x) = u/v,
con u = lnx, cuya derivada queda expresada: u ' = 1/x, y
con v = ex, cuya derivada queda expresada: v ' = ex.
Luego, plantea la regla del cociente:
f ' (x) = [ u ' * v - u * v ' ] / v2,
luego sustituyes expresiones, y queda:
f ' (x) = [ (1/x)*ex - lnx*ex ] / (ex)2,
luego, extraes factor común en el numerador, y queda:
f ' (x) = ex*[ 1/x - lnx ] / (ex)2,
simplificas expresiones exponenciales, y queda:
f ' (x) = [ 1/x - lnx ] / ex.
Espero haberte ayudado.
-
Hola, quisiera que me ayuden con el análisis de esta función.
Dominio, Rango, continuidad, signo, máximo mínimo, extremos relativos. gracias.f(x)=x^(-x) equis elevado a la menos equis
Antonio Silvio Palmitano
el 22/12/17Puedes comenzar por reescribir la expresión en forma exponencial:
f(x) = x-x = (elnx)-x = e-x*lnx, y observa que el dominio de la función es: D = (0,+∞).
Luego, plantea la expresión de la función derivada primera (observa que debes aplicar la regla de la cadena y a regla del producto):
f ' (x) = e-x*lnx*(-lnx - 1) = -e-x*lnx*(lnx + 1), observa que está definida en todo el dominio de la función.
Luego, plantea la condición de punto crítico (posible máximo o posible mínimo):
f ' (x) = 0, sustituyes la expresión de la función derivada en el primer miembro, y queda:
-e-x*lnx*(lnx + 1) = 0, haces pasaje del factor exponencial (recuerda que toma valores estrictamente positivos) como divisor, y queda:
-(lnx -+ 1) = 0, multiplicas en todos los términos de la ecuación por -1, y queda:
lnx + 1 = 0, haces pasaje de término, y queda:
lnx = - 1, compones en ambos miembros con la función inversa del logaritmo natural, y queda:
x = e-1 ≅ 0,368.
Luego, divides el dominio en intervalos, eliges un representante en cada uno de ellos y evalúas el signo que toma la función derivada primera:
I1 = (0,e-1), representado por x = 0,1, y para él la función derivada primera toma el valor: f ' (0,1) = -e-0,1*ln(0,1)*(ln(0,1) + 1) ≅ 1,640 > 0,
por lo que tienes que la función es creciente en este intervalo;
I2 = (e-1,+∞), representado por x = 1, y para él la función derivada primera toma el valor: f ' (1) = -e-1*ln(1)*(ln(1) + 1) = -1 < 0,
por lo que tienes que la función es decreciente en este intervalo;
luego, puedes concluir que la función alcanza un máximo en x = e-1, y el valor de la función para él es: f(e-1) =e^(e-1*ln(e-1)) ≅ 0,692.
Espero haberte ayudado.
-
Alguien sabría calcular el Área de cada triángulo pequeño, sabiendo que el triángulo grande ABC es rectángulo y que los puntos D, E y F dividen la hipotenusa BC en 4 partes iguales?
Antonius Benedictus
el 22/12/17Daniel Freire
el 22/12/17Veamos... mmm te fice el ejercicio que encuentres la hipotenusa... pues usa pitagoras h^2= c^2+c^2
Te esta diciendo que d e y f esta cortados en partes iguales... pues lo hace mas facil aun...
Al sacar la hipotenusa lo divides para 3 entonces ya tendrias 4 catetos y 2 hipotenusas... pero dices que solo quieres los triangulos D E y F entonces usas de nuevo pitagoras despejas la formula y te quedara de esta manera raiz de h^2-c^2=c
Ahora que tienes la formula... la resuelves a cada uno de los triangulos... cuando tengas los lados de cada triangulo sacas el area que seria...
A=((base)(altura))/2
Y tendras que hacer en cada triangulo de nuevo el teorema de pitagoras para formar un triangulo rectangulo y sacar la altura... en fin aqui no te puedo ecplicar bien pero te di todas las herramirntas para resolver tu tarea. Suerte
-
Ángel
el 22/12/17Daniel Freire
el 22/12/17
La otra manera de presentar esa raiz es es de la siguiente forma vamos a suponer que esto simbolo (₩) es la raiz porque no tengo en el teclado
Entonses seria asi
₩5+₩5
₩₩5^2+5
₩₩25+5
₩₩30
^4₩30 Esta es la una forma de expresarla
Y esta es la otra forma
30^1/4
Si no sabes que significa "^" es el exponente... se usa en calculadoras cientificas para expresar un exponente... espero te aya ayudado
-
Antonio Silvio Palmitano
el 22/12/17a)
Tienes que la región está limitada por dos curvas, cuyas ecuaciones son:
x2 + y2 = 36, que corresponde a una circunferencia con centro: C(0,0) y radio: R = 6,
y2 = 9x, que corresponde a una parábola con vértice: V(0,0), y eje de simetría OX positivo.
Luego, restas miembro a miembro entre ambas ecuaciones y queda:
x2 = 36 - 9x, haces pasajes de términos, y queda:
x2 + 9x - 36 = 0, que es una ecuación polinómica cuadrática, cuyas soluciones son:
x1 = -12, que no corresponde a un punto perteneciente a la parábola (recuerda que su eje de simetría es OX positivo);
x2 = 3, que al reemplazar en la ecuación de la parábola queda:
y2 = 27, haces pasaje de potencia como raíz, y tienes dos opciones:
ya = -√(27), por lo que tienes el punto: A( 3 , -√(27) ), que puedes verificar pertenece a las dos curvas;
yb = √(27), por lo que tienes el punto: B( 3 , √(27) ), que puedes verificar pertenece a las dos curvas.
Luego, haz un gráfico, y podrás observar que la región está limitada "por la izquierda" por la paraábola, y "por la derecha" por la circunferencia,
por lo que puedes plantear elementos horizontales de área para integrar, y para ello planteas las ecuaciones explícitas para x en ambas curvas, y quedan:
x = √(36 - y2), y observa que elegimos el signo positivo por tratarse de la semicircunferencia "derecha",
x = y2/9, que corresponde a la parábola.
Luego, plantea para el área:
A = ∫ [ √(36 - y2) - y2/9 ]*dy, para evaluar con Regla de Barrow entre: ya = -√(27) e yb = √(27).
Luego, queda que integres cada término por separado, y observa que para el primer término puedes emplear la sustitución (cambio de variable): y = 6*senw, y observa que la integral del segundo término es directa.
Haz el intento, y si te resulta necesario, no dudes en volver a consultar.
Espero haberte ayudado.
-
ANTES DE IROS DE VACACIONES! Que alguien resuleva esto urgentemente, no es dificil pero muy necesario...
Antonio Silvio Palmitano
el 22/12/17Recuerda una de las propiedades del valor absoluto con las desigualdades:
|u| < a es equivalente a: -a < u < a (1).
Luego, aplicas la propiedad señalada (1), y la inecuación de tu enunciado queda:
-4 < x2 - |3+2x| < 4.
Luego, aplicas la definición de valor absoluto y tienes dos opciones:
a)
3 + 2x ≥ 0, haces pasaje de término, y luego de factor como divisor, y queda: x ≥ -3/2 (2);
luego, sustituyes (observa que el argumento del valor absoluto es positivo), y la doble inecuación queda:
-4 < x2 - (3+2x) < 4, distribuyes el signo en el agrupamiento, ordenas términos, y queda:
-4 < x2 - 2x - 3 < 4, sumas 4 en los tres miembros de la doble inecuación, y queda:
0 < x2 - 2x + 1 < 8, factorizas el trinomio cuadrado perfecto en el miembro central, y queda:
0 < (x-1)2 < 8;
luego, observa que la primera desigualdad se verifica para x ≠ 1 (3),
y en la segunda desigualdad haces pasaje de potencia como raíz (observa que el exponente es par), y queda:
|x-1| < √(8), aplicas la propiedad señalada (1), y queda:
-√(8) < x - 1 < √(8), sumas 1 en los tres miembros de la doble inecuación, y queda:
-√(8) + 1 < x < √(8) + 1 (4);
luego, el subintervalo solución para esta opción, cuyos elementos cumplen las condiciones señaladas (2) (3) (4) queda:
Ia = ( -3/2 , 1 ) u ( 1 , √(8)+1 );
b)
3 + 2x < 0, haces pasaje de término, y luego de factor como divisor, y queda: x < -3/2 (5);
luego, sustituyes (observa que el argumento del valor absoluto es negativo), y la doble inecuación queda:
-4 < x2 - [-(3+2x)] < 4, distribuyes los signos en el agrupamiento, ordenas términos, y queda:
-4 < x2 + 2x + 3 < 4, restas 2 en los tres miembros de la doble inecuación, y queda:
-6 < x2 + 2x + 1 < 2, factorizas el trinomio cuadrado perfecto en el miembro central, y queda:
-6 < (x-1)2 < 2;
luego, observa que la primera desigualdad se verifica para todo x real, ya que su primer miembro es estrictamente negativo y sus segundo miembro es positivo,
y en la segunda desigualdad haces pasaje de potencia como raíz (observa que el exponente es par), y queda:
|x-1| < √(2), aplicas la propiedad señalada (1), y queda:
-√(2) < x - 1 < √(2), sumas 1 en los tres miembros de la doble inecuación, y queda:
-√(2) + 1 < x < √(2) + 1 (6);
luego, el subintervalo solución para esta opción, cuyos elementos cumplen las condiciones señaladas (5) (6) queda:
Ib = ( -√(8)+1 , -3/2 ).
Luego, plantea el intervalo solución como la unión de los subintervalos:
I = Ib u Ia = ( -√(8)+1 , -3/2 ) u ( -3/2 , 1 ) u ( 1 , √(8)+1 ).
Espero haberte ayudado.
-
Hola ¿Me pueden decir paso a paso cómo queda la siguiente ecuación trigonométrica? (también pone que se simplifique el resultado):
- sen 2x - cos x = 0
lo que hice fue aplicar la razón del ángulo doble al sen 2x, luego de eso con la identidad fundamental de la razón trigonométrica (sen2α + cos2α = 1) despejé sen2α para que la operación sólo me quede en cosenos y me quedó
- 2(√1 - cos2x) cos x - cos x = 0
Como hay una raíz cuadrada elevé al cuadrado todos los factores:
- (2)2([√1 - cos2x])2 (cos x)2- (cos x)2= 0
- = 4 (1-cos4x) cos2x - cos2x = 0
- =4 - 4 cos4x cos2x - cos2x = 0
Y ya me estanqué no se cómo seguir, es decir, lo sé pero se me ocurren muchas maneras de hacerlo, una que se me ocurrió fué:
- cómo -4 cos4x cos2x se están multiplicando sumé sus potencias quedando:
- -4 cos6x - cos2x + 4 (← ese +4 lo pasé al final por que me es cómodo, quedando casi como una ecuación de segundo grado)
Pero no sé si ese último paso está bien, luego ya no sé que hacer. Me gustaría que me lo explicarán al detalle, si les sobra tiempo pongan notas en lo ejercicios de lo que están haciendo. De antemano, Muchas Gracias.
Antonio Silvio Palmitano
el 22/12/17Has comenzado bien, al aplicar la identidad del seno del doble de un ángulo, y la ecuación queda:
2*senx*cosx - cosx = 0,
luego, observa que puedes extraer factor común, y queda:
cosx*(2*senx - 1) = 0,
luego, por anulación de un producto, tienes dos opciones:
a)
cosx = 0, aquí compones con la función inversa del coseno, y queda:
x = ±90°+180°*k, con k ∈ Z (en grados);
b)
2*senx - 1 = 0, haces pasaje de término, y queda:
2*senx = 1, haces pasaje de factor como divisor, y queda:
senx = 1/2,
luego compones con la función inversa del seno, y tienes dos opciones:
b1)
x = 30°+360°*m, con m ∈ Z (en grados, en el primer cuadrante),
b2)
x = 150°+360°*n, con n ∈ Z (en grados, en el segundo cuadrante),
Espero haberte ayudado.