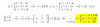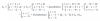Pon foto del enunciado original, por favor.

No hace falta:

Ecuaciones de rectas y planos

Antonio, he visto los vídeos pero no logro entenderlos del todo :|

Pues plantea la duda acerca de un ejercicio. No nos coloques un boletín completo.

Perdón me expresé mal. No entiendo los ejercicios 18 y 24.

24)

18)

Tienes la ecuación diferencial de primer orden y segundo grado:

y = 3*x*dy/dx + 6*(dy/dx)²*y².

Luego, planteas la sustitución (cambio de función):

dy/dx = p (1), de donde tienes: 1/p = dxdy (2);

luego sustituyes y queda:

y = 3*x*p + 6*p²*y² (*);

haces pasaje de término, y queda:

y - 6*p²*y² = 3*x*p,

divides en todos los términos de la ecuación por p, y queda:

y/p - 6*p*y² = 3*x,

expresas el primer término como un producto, y queda:

y*p^-1 - 6*p*y² = 3*x,

derivas implícitamente con respecto a y, y queda:

p^-1 - y*p^-2*(dp/dy) - 6*(dp/dy)*y² - 12*p*y = 3*(dx/dy),

sustituyes la expresión señalada (2) en el segundo miembro, y queda:

p^-1 - y*p^-2*(dp/dy) - 6*(dp/dy)*y² - 12*p*y = 3*(1/p),

que es una ecuación diferencial de primer orden y de primer grado;

luego, multiplicas en todos los términos de la ecuación por p², y queda:

p - y*(dp/dy) - 6*(dp/dy)*p²*y² - 12*p³*y = 3*p,

haces pasaje de término, ordenas términos, y queda:

- 2*p - 12*p³*y - y*(dp/dy) - 6*(dp/dy)*p²*y² = 0,

extraes factores comunes por grupos, y queda:

- 2*p*(1 + 6*p²*y) - y*(dp/dy)*(1 + 6*p²*y) = 0,

extraes factor común, y queda:

(1 + 6*p²*y)*( -2*p - y*(dp/dy) ) = 0,

luego, por anulación de un producto, tienes dos opciones:

1)

1 + 6*p²*y = 0, haces pasaje de término, y queda:

6*p²*y = - 1, multiplicas en ambos miembros de la ecuación pro y^-1/6, y queda:

p² = - y^-1/6, y observa que si haces pasaje de potencia como raíz te queda una expresión con coeficiente complejo, por lo que consideras que esta opción no conduce a soluciones que sean funciones cuyas expresiones tengan coeficientes reales;

2)

-2*p - y*(dp/dy) = 0, haces pasaje de término, y queda:

- y*(dp/dy) = 2*p, separas variables, y queda:

dp/p = - 2*dy/y, integras en ambos miembros, y queda:

ln|p| = - 2*ln|y| + C,

aplicas la propiedad del logaritmo de una potencia, expresas a la constante como un logaritmo, y queda:

ln|p| = ln|y^-2| + ln|K|, aplicas la propiedad del logaritmo de un producto, y queda:

ln|p| = ln|K*y^-2|, compones en ambos miembros con la función inversa del logaritmo natural, y queda:

p = K*y^-2.

Luego, sustituyes en la ecuación señalada (*), y queda:

y = 3*x*K*y^-2 + 6*(K*y^-2)²*y², 

ordenas factores y resuelves potencias en los términos, y queda:

y = 3*K*x*y^-2 + 6*K²*y^-2,

y = 3*K*x/y² + 6*K²/y²,

multiplicas en todos los términos de la ecuación por y², y queda:

y³ = 3*K*x + 6*K²,

que es una solución general implícita de la ecuación diferencial que tienes en tu enunciado.

Espero haberte ayudado.

Recta tangente con derivación implícita

Por favor, envía foto del enunciado si luego del ver el vídeo sigues necesitando ayuda.

No salimos a enlaces externos.

Observa que tienes una población de tamaño n = 12, en la que tienes 4 esferas verdes y 8 esferas de otros colores.

Luego, la probabilidad de extraer una esfera verde es: p = 4/12 = 1/3, y la probabilidad de extraer una esfera de otro color es q = 8/12 = 2/3.

Luego, observa que a variable aleatoria puede tomar los valores: 0 1, 2, 3 o 4.

Luego, tienes una variable aleatoria discreta con distribución binomial, con parámetros: n = 12, p = 1/3, con probabiidad complementaria: q = 2/3: y la expresión:

p(X = k) = C(4.k)*(1/3)^k*(2/3)^4-k, corresponde a la función de distribución de probabilidad de la variable aleatoria.

Luego, tienes:

p(X = 2) = C(4,2)*(1/3)²*(2/3)² = ( 4!/(2!*2!) )*(1/9)*(4/9) = 6*4/81 = 8/27;

p(X = 0) = C(4,0)*(1/3)⁰*(2/3)⁴ = ( 4!/(0!*4!) )*(1)*(16/81) = 1*16/81 = 16/81;

p(X = 4) = C(4,4)*(1/3)⁴*(2/3)⁰ = ( 4!/(4!*0!) )*(1/81)*(1) = 1*1/81 = 1/81.

Espero haberte ayudado.

Muchas gracias por su explicación!!!

Tienes la ecuación:

π*r*√(r2 + h2) = S, en la que S es constante, y puedes suponer que esa ecuación define a h como función de r;

luego, haces pasaje de factor como divisor, y queda:

r*√(r2 + h2) = S/π (observa que el segundo miembro es constante);

luego, elevas al cuadrado en ambos miembros, y queda:

( r*√(r2 + h2) )² = (S/π)² (observa que el segundo miembro es constante);

luego, distribuyes la potencia en el primer miembro (observa que tienes simplificación en el segundo factor), y queda:

r²*(r2 + h2) = (S/π)², distribuyes en el primer miembro, y queda:

r4 + r²*h2 = (S/π)², y observa que el segundo miembro es constante.

Luego, puedes derivar implícitamente con respecto a r, y queda:

4r³ + 2r*h² + r²*2h*(dh/dr) = 0, divides por 2r (observa que r toma valores estrictamente positivos) en todos los términos de la ecuación, y queda:

2r² + h² + r*h*(dh/dr) = 0, haces pasajes de términos, y queda:

r*h*(dh/dr) = - 2r² - h², divides por r*h en todos los miembros de la ecuación (observa que r y h toman valores estrictamente positivos), y queda:

dh/dr = - 2r/h - h/r.

Espero haberte ayudado.

Revisa las operaciones. el procedimiento es correcto: