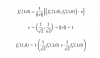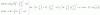-
Raisa
el 23/11/17 -
Paola Guerrero
el 23/11/17Si los coeficientes de dividir P(x) entre (x+1) y (x-2) son respectivamente : Q(x) y R(x) , determine P(3) sabiendo que : P(1)=3 , P(2)=2 ; 2Q(3)+R(3)=5
Hola unicoos , necesito ayuda con este ejercicio , disculpe las molestias
-
Bomba!!!
el 23/11/17Hola , me podrian ayudar con el ejercicio Gracias
Calcular P(x) con los minimos coeficientes enteros si P(-3)=0
P(ax)=(a^3)(x^2)+abx+a ; a>0 , b>0 , b>a
Hallar: P(5)
Antonio Silvio Palmitano
el 24/11/17Tienes los datos:
P(-3) = 0,
P(ax) = a3x2 + abx + a.
Luego, evalúas para x = -3/a, y queda:
P(-3) = a3(-3/a)2 + ab(-3/a) + a, reemplazas en el primer miembro, resuelves términos en el segundo miembro, y queda:
0 = 9a - 3b + a, reduces términos semejantes, haces pasaje de término, y queda:
3b = 10a, haces pasaje de factor como divisor, y queda:
b = 10a/3 (1).
Luego, sustituyes la expresión señalada (1) en el segundo término de la expresión del polinomio, y queda:
P(ax) = a3x2 + a(10a/3)x + a, resuelves el segundo término, y queda:
P(ax) = a3x2 + (10a2/3)x + a,
luego, reemplazas el valor: a = 1 (observa que para este valor corresponde: b = 10/3), y queda:
P(1x) = 13x2 + (10(1)2/3)x + 1,
resuelves factores, resuelves términos, resuelves el argumento en el primer miembro, y queda:
P(x) = x2 + (10/3)x + 1.
y observa que se cumplen las condiciones que tienes en tu enunciado: a > 0, b > 0, b > a.
Espero haberte ayudado.
-
Juan
el 23/11/17¿Cómo calculo la recta tangente a y=x-ln(y) en el punto (3,1)?
Juan
el 23/11/17 -
Gonzalo Acosta
el 23/11/17
Como justifico si es continua? (A) y como hago el punto C?
Disculpe las molestias.
Gonzalo Acosta
el 23/11/17Gonzalo Acosta
el 23/11/17 -
Luis
el 23/11/17X+ay+0z=a
-2x-a-1y+z=b
X+2a-1y+a+2z=c
Como se resolvería ese sistema?
Me interesa la parte de la matriz de ampliada para ver la relación de los dos parámetros
-
Arnau Planas
el 23/11/17Buenas noches. ¿Me podrían ayudar con este problema de optimización? Muchas gracias.
En un triángulo isóceles de base 24 cm y altura 20 cm se inscribe un rectángulo. ¿Cúales tienen que ser sus dimensiones para que el área sea máxima?
-
Usuario eliminado
el 23/11/17algueien me podría ayudar a resolver este problema...
Dos máquinas rectificadoras A y B trabajan de tal manera que cuando se ajusta el diámetro requerido para la pieza rectifican según una distribución normal de media 5 mm y desvíos 0,01 y 0,02 mm respectivamente. La máquina A hace el 80% del trabajo y la B el resto. Se mezclan la piezas rectificadas y se supone que una pieza es buena si el diámetro D de una pieza está comprendido entre 5 mm y 5,02 mm.
a) ¿Cuál es la prob. de que una pieza elegida al azar no cumpla con la especificación?
El resultado es 0,55
-
Catherine
el 23/11/17
-
Marest
el 23/11/17Me pueden ayudar por favor?
Problema: Un depósito contiene 600 m3 de agua. Para regar una finca se extraen el lunes los 2/5 del depósito y el martes 1/3 del agua que quedaba. ¿Qué cantidad de agua se sacó cada día?¿Cuántos litros de agua quedarán el miércoles en el depósito?¿Qué fracción del depósito quedará el miércoles?
Muchas gracias.
Antonio
el 23/11/17lunes: se extraen los 2/5 del depósito, es decir, se extraen los 2/5 de 600 m3, es decir, se extraen 240 m3
martes: se extraen los 1/3 del agua que quedaba, es decir, se extraen 1/3 de (600-240) m3, es decir, se extraen 1/3 de 360 m3, es decir, se extraen 120 m3
miércoles: quedan 360- 120 = 240 m3, es decir, 240/600 = 2/5
Ángel
el 23/11/17El Lunes se extraen 2/5 del depósito----> 600-[(2/5)*600] = 600 - 240 = 360 (observa que se extraen 240 m3 el Lunes y quedan 360 m3)
y el Martes 1/3 del agua que quedaba -----> 360-[(1/3)*360] = 360 - 120= 240 (observa que se extraen 120 m3 el Martes y quedan 240 m3el Miércoles en el depósito)
La fracción del depósito quedará el miércoles es 240/600= 6/15 = 2/5
