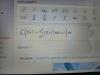
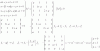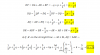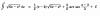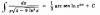-
Hola, me podríais explicar el principio de inducción, y un ejemplo resuelto por favor, por ejemplo me lo podríais explicar con este: si n>=2 ----- n^3>=n^2+3.
muchas gracias
César
el 21/10/17Antonius Benedictus
el 21/10/17Antonio Silvio Palmitano
el 21/10/17Tienes la proposición:
P(n): n3 ≥ n2 + 2, ∀n ∈ N, n ≥ 2.
1°)
Probamos para el primer elemento (n = 2):
P(2): 23 ≥ 22 + 2, resuelves en ambos miembros y queda: 8 ≥ 6, que es una desigualdad Verdadera.
2°)
P(h): h3 ≥ h2 + 2, ∀h ∈ N, h ≥ 2 (Hipótesis Inductiva, que se acepta como Verdadera).
3°)
P(h+1): (h+1)3 ≥ (h+1)2 + 2, ∀n ∈ N, n ≥ 2 (Tesis Inductiva, que debe ser demostrada).
4°)
Demostración:
P(h+1): (h+1)3 = h3 + 3h2 + 3h + 1 ≥
aplicas la Hipótesis Inductiva, y queda:
≥ h2 + 2 + 3h2 + 3h + 1 =
sumas y restas 2h, sumas y restas 1, ordenas términos, agrupas términos, y queda:
= (h2 + 2h + 1) + 2 + (3h2 + 3h + 1 - 2h - 1) =
factorizas el trinomio cuadrado perfecto, reduces términos semejantes en el segundo agrupamiento (observa que tienes cancelaciones, y queda:
= (h + 1)2 + 2 + (3h2 + 3h) =
extraes factores comunes en el agrupamieto, y queda:
= (h + 1)2 + 2 + 3h(h + 1) ≥
restas 3h(h + 2) (observa que esta expresión es positiva, por ser producto de tres factores naturales), y queda:
≥ (h + 1)2 + 2 + 3h(h + 1) - 3h(h + 1) =
= (h + 1)2 + 2;
luego, por la cadena de igualdades y desigualdades, tienes que la Tesis Inductiva es Verdadera.
Espero haberte ayudado.
-
resolver para el valor de a un sistema homogéneo con solución distinta a la trivial
ax+y+z+t=0
x+(1+a)y+z+t=0
x+y+(2+a)z+t=0
x+y+z+t=0
-
por favor ayuda como resuelvo esto:
2/3 +5/2 .6/5 +1/3 =
3/2 : (5/6 - 2/3)
Antonio Silvio Palmitano
el 21/10/171)
Tienes en tu segundo término: (5/2)*(6/5) = (5*6)/(2*5) = 30/10 = simplificas por 10 = 3/1;
luego reemplazas, y la expresión queda:
2/3 + 3/1 + 1/3 = multiplicas por 3 al numerador y al denominador del segundo término, y queda:
= 2/3 + 9/3 + 1/3 = (2 + 9 + 1)/3 = 12/3 = simplificas por 3 = 4/1 = 4.
2)
Tienes en el agrupamiento:
5/6 - 2/3 = multiplicas por 2 al numerador y al denominador del segundo término = 5/6 - 4/6 = (5 - 4)/6 = 1/6,
luego reemplazas, y la expresión queda:
(3/2) : (5/6 - 2/3) = (3/2) : (1/6) = (3/2)*(6/1) = (3*6)/(2*1) = 18/2 = simplificas por 2 = 9/1 = 9.
Espero haberte ayudado.
-
Necesito ayuda en un ejercicio, "Haya todas las matrices X que cumplan A•X=X•A, siendo
A= ( 1 1
0 1)
Antonio Silvio Palmitano
el 21/10/17Puedes plantear la matriz incógnita:
X =
x y
z w.
Luego, plantea los productos:
a)
A*X =
1 1 x y
0 1 * z w
resuelves y queda:
A*X =
(x+z) (y+w)
z w
b)
X*A =
x y 1 1
z w * 0 1
resuelves, y queda:
X*A =
x (x+y)
z (z+w)
Luego, igualas elemento a elemento en las matrices remarcadas, y tienes el sistema de ecuaciones:
x + z = x, aquí haces pasaje de término, y queda: z = 0
y + w = x + y, aquí haces pasaje de término, y queda: w = x
z = z, aquí haces pasaje de término, y queda: 0 = 0, que es una identidad verdadera
w = z + w, aquí haces pasaje de término, y queda: z = 0;
por lo tanto, tienes que el sistema de ecuaciones admite infinitas soluciones, que quedan expresadas:
x ∈ R,
y ∈ R,
z = 0,
w = x.
Luego, la matriz incógnita queda:
X =
x y x y
z w = 0 x, con x ∈ R e y ∈ R.
Espero haberte ayudado.
-
hola!!! Q tal ... Me podrían ayudar a desarrollar estas integrales es que ya no esta en mis conocimientos.... Saludos desde Mexico
Antonio Silvio Palmitano
el 21/10/17Vamos con una orientación para la segunda integral.
Aplica la sustitución (cambio de variable): w = lnx, de donde tienes: dw = dx/x, luego sustituyes, y la integral queda:
I = ∫ ( 1 / √(4-9*w2) )*dw,
luego, tienes el argumento de la raíz cuadrada:
4 - 9*w2 = 4*(1 - 9*w2/4) = 4*( 1 - (3*w/2)2 ), planteas su raíz cuadrada, y queda: √( 4*( 1 - (3*w/2)2 ) ) = 2*√( 1 - (3*w/2)2 );
luego, sustituyes, y la integral queda:
I = (1/2) * ∫ ( 1 / √( 1 - (3*w/2)2 ) )*dw,
luego, aplica la sustitución (cambio de variable):
3*w/2 = p, de donde tienes: 3*dw/2 = dp, y también tienes: dw = (2/3)*dp, luego sustituyes, y la integral queda:
I = (1/2)*(2/3) * ∫ ( 1 / √(1-p2) )*dp = resuelves = (1/3) * arcsen(p) + C,
luego sustituyes según el último cambio de variable, y queda:
I = (1/3) * arcsen(3*w/2) + C;
luego sustituyes según el primer cambio de variable, y queda:
I = (1/3) * arcsen(3*lnx/2) + C = aplicas la propiedad del logaritmo de una potencia = (1/3) * arcsen( ln(x3/2) ) + C.
Espero haberte ayudado.
-
Gracias Angel los tutoriales k me han mandado estan genial ,la verdad me han ayudado bastante pero no termino de coger las multiplicaciones ,divisiones de fracciones pero con parentesis y corchetes tengo examen proximamente y en los videos k me mandastes no me explica como se hacen con parentesis ,necesito saber como se hace las fracciones con parentesis sobre todo multiplicaciones y divisiones .bueno en general con las cuatro aplicaciones basicas ,suma resta multiplicacion y division de fracciones con parentesis
gracias
-
Hola a todos necesito que me ayuden porfavor en estos 2 problemas (el 11 y el 14)
 para entenderle al tema de multiplicadores de lagrange que van a venir en mi examen del Lunes.
para entenderle al tema de multiplicadores de lagrange que van a venir en mi examen del Lunes.Espero que me puedan ayudar. GRACIAS
Antonio Silvio Palmitano
el 21/10/1711)
Plantea la función "distancia cuadrática" entre un punto genérico P(x,y,z) y el punto A(2,3,4):
f(x,y,z) = (x-2)2 + (y-3)2 + (z-4)2;
observa que es una función diferenciable en R3, cuyas derivada parciales quedan:
fx = 2*(x-2) = 2*x - 4,
fy = 2*(y-3) = 2*y - 6,
fz = 2*(z-4) = 2*z - 8.
Luego, observa que la esfera es una superficie de nivel de la función diferenciable en R3 cuya expresión es:
g(x,y,z) = x2 + y2 + z2,
cuyas derivadas parciales quedan:
gx = 2*x,
gy = 2*y,
gz = 2*z.
Luego, plantea el sistema de ecuaciones de Lagrange (indicamos con p al multiplicador):
2*x - 4 = p*2*x
2*y - 6 = p*2*y
2*z - 8 = p*2*z
x2 + y2 + z2 = 9,
con p ∈ R.
divides por 2 en todos los términos de las tres primeras ecuaciones, y el sistema queda:
x - 2 = p*x
y - 3 = p*y
z - 4 = p*z
x2 + y2 + z2 = 9,
con p ∈ R.
Observa que tanto x, como y, como z deben ser distintos de cero, porque si alguna de ellas es igual a cero no se verifica alguna de las tres primeras ecuaciones;
por lo tanto, puedes dividir por x en todos los términos de la primera ecuación, por y en todos los términos de la segunda ecuación, y por z en todos los términos de la tercera
ecuación, y el sistema queda:
1 - 2/x = p (1)
1 - 3/y = p
1 - 4/z = p
x2 + y2 + z2 = 9,
con p ∈ R.
Luego, sustituyes la expresión señalada (1) en las demás ecuaciones, haces pasajes de términos en las dos primeras (observa que tienes cancelaciones, y queda:
2/x = 3/y, de aquí despejas: y = 3x/2 (2)
2/x = 4/z, de aquí despejas: z = 2x (3)
x2 + y2 + z2 = 9,
con p ∈ R.
Luego, sustituyes las expresiones señaladas (2) (3) en la última ecuación, resuelves en cada término, y queda:
x2 + 9x2/4 + 4x2 = 9, reduces términos semejantes, y queda:
29x2/4 = 9, de aquí despejas:
x2 = 36/29, haces pasaje de potencia como raíz, y tienes dos opciones:
a)
x = -6/√(29), reemplazas en las ecuaciones señaladas (2) (3) (1) y queda: y = -9/√(29), z = -12/√(29), p = 1 + √(29)/3,
que son las coordenadas del primer punto crítico, con su multiplicador;
b)
x = 6/√(29), reemplazas en las ecuaciones señaladas (2) (3) (1) y queda: y = 9/√(29), z = 12/√(29), p = 1 - √(29)/3,
que son las coordenadas del segundo punto crítico, con su multiplicador.
Luego, queda que evalúes la expresión de la función para estos dos puntos críticos para identificar en cuál de ellos la función toma valor Máximo Absoluto, y en cuál de ellos
toma valor Mínimo Absoluto.
Espero haberte ayudado.
Antonio Silvio Palmitano
el 21/10/1714)
Considera que el origen de coordenadas es uno de los vértices de la base, y considera que la caja tiene altura z, por lo que tienes para las coordenadas del vértice P, opuesto por la diagonal al origen de coordenadas: P(x,y,z). y observa que este punto pertenece al plano cuya ecuación tienes en el enunciado. Observa que con este planteo, tienes que las coordenadas corresponden al ancho, al largo y a la altura de la caja, por lo que tienes que las tres coordenadas toman valores estrictamente positivos.
Luego, plantea la expresión del volumen de la caja:
f(x,y,z) = x*y*z,
observa que es la expresión de una función diferenciable en R3, cuyas derivada parciales quedan expresadas:
fx = y*z
fy = x*z
fz = x*y.
Luego, observa que el plano es una superficie de nivel de la función diferenciable en R3 cuya expresión es:
g(x,y,z) = 2x + 3y + 4z, cuyas derivadas parciales quedan expresadas:
gx = 2
gy = 3
gz = 4.
Luego, plantea el Sistema de Ecuaciones de Lagrange (observa que indicamos con p al multiplicador):
y*z = 2*p, de aquí despejas: y*z/2 = p (1)
x*z = 3*p
x*y = 4*p
2x + 3y + 4z = 12
p ∈ R.
Luego, sustituyes la expresión señalada (1) en las demás ecuaciones, y queda:
x*z = 3*y*z/2, aquí divides en ambos miembros por z (recuerda que toma valores estrictamente positivos), y queda: x = 3*y/2 (2)
x*y = 2*y*z
2x + 3y + 4z = 12
p ∈ R.
Luego, sustituyes la expresión señalada (2) en las demás ecuaciones, y queda:
3*y2/2 = 2*y*z, aquí haces pasajes de factores como divisores (recuerda que y toma valores estrictamente positivos), y queda: 3*y/4 = z (3)
6y + 4z = 12
Luego, sustituyes la expresión señalada (3) en la última ecuación, y queda:
9y = 12, aquí haces pasaje de factor como divisor, y queda: y = 4/3;
luego, sustituyes en las ecuaciones señaladas (3) (2) (1), y queda: z = 1, x = 2, p = 2/3,
que son las coordenadas del punto crítico con su multiplicador.
Luego, evalúas en la función, y queda:
V = 2*(4/3)*1 = 8/3, que es el valor del volumen máximo.
Puedes verificar que se trata de un valor máximo de la función, evaluándola en un punto testigo perteneciente al plano, por ejemplo: T(5/2,1,1):
V(5/2,1,1) = (5/2)*1*1 = 5/2 < 8/3, por lo que tienes que la función, para el punto testigo, toma valor menor que en el punto crítico.
Espero haberte ayudado.