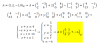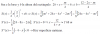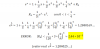-
Rodrigo Ivan Saez
el 21/10/17La funcion f(x,y,z): es una funcion f: R3 -> R2 , tal que x+y>0, y z≠-3 (tiene restricciones en el dominio). Definido mas riguroso: f: A={(x,y,z)∈R3 | x+y>0 ∧ z≠-3} --> D1
(D1⊆R3)
La funcion g(u,v): g: R2 -> R, tal que v≥0, mas riguroso g: B={(u,v)∈R2 | v≥0} --> D2
(D2⊆R)
Donde D1 y D2 son los recorridos de ambas funciones, y A y B los dominios de ambas funciones.
En principio se puede ver que "se podria" componer una funcion (g ο f) : R3 ->R, pero debemos comprobar que: D1 ⊆ B:
Para ver esto, dado que tenemos "esta posible" funcion compuesta tal que:
u = Ln(x+y)/(z+3)
v = x^2 e^x
Vemos que "u" no tiene restricciones, por tanto no hay problema. Sin embargo "v" si tiene la restriccion v≥0, pero como v=x^2 e^x, y ambas funciones son siempre positivas o iguales a cero, tampoco tenemos problemas con esta coordenada. Luego, podemos componer la funcion (g ο f)
-
Hola unicoos. No sé cómo hacer este ejercicio. Hice de este estilo pero con vectores, no matrices. y no se me ocurre como puedo hacerlo😔

chado
el 20/10/17Sos de la UNLaM? :o :o :o
se que es de universidad ese tema y no se responde aqui
pero se que con ese datos que te dieron, lo interpretas como que son las coodenadas,osea k(1,2,-1,0)=(k,2k,-k,0) ahora esos escalares los multiplicas por la base B, pero si podrias subir el enunciado completo seria mejor :D
-
Holaa, alguien me ayuda en este ejercicio:
Una ventana tiene forma rectangular con un semícirculo de vidrio coloreado. El coloreado solo transmite la mitad de luz por metro cuadrado que el claro. Si el perimetro de la ventana es de 16 metros, determinar las propiedades de la ventana que admitirá más luz.
Ángel
el 20/10/17Pablo Molina
el 20/10/17Antonio Silvio Palmitano
el 20/10/17Puedes llamar:
2x, al ancho de la ventana rectangular;
2y, a la altura de la ventana rectangular.
Luego, si el diámetro del semicírculo coincide con el ancho de la ventana rectangular,
tienes que su radio es x.
Luego, plantea que la cantidad de luz por unidad de área que transmite la ventana rectangular es Y,
por lo que tienes que la cantidad de luz por unidad de área que transmite el semicírculo coloreado es Y/2.
Luego, plantea las cantidades de luz transmitidas:
Por la ventana rectancular: LR = Y*AR = Y*2x*2y = 4*Y*x*y;
Por el semicírculo coloreado: LS = (Y/2)*π*x2/2 = (1/4)*Y*π*x2.
Luego, la cantidad total de luz transmitida queda expresada:
L = LR + LS, sustituyes expresiones, y queda:
L = 4*Y*x*y + (1/4)*Y*π*x2 (1),
que es la expresión de la cantidad total de luz transmitida en función del semiancho de la ventana rectangular (y radio del semicírculo coloreado), y de la altura de la ventana rectangular.
Luego, plantea la expresión del perímetro de la ventana rectangular:
2*(2x) + 2*(2y) = 16, resuelves coeficientes, y queda:
4*x + 4*y = 16, divides en todos los términos de la ecuación por 4, y queda:
x + y = 4, haces pasaje de término, y queda:
y = 4 - x (2),
luego, sustituyes la expresión señalada (2) en la expresión de la función señalada (1), y queda:
L = 4*Y*x*(4 - x) + (1/4)*Y*π*x2,
distribuyes el primera término, y queda:
L = 16*Y*x - 4*Y*x2 + (1/4)*Y*π*x2,
Luego, plantea la expresión de la función derivada primera, y queda:
L ' = 16*Y - 8*Y*x + (1/2)*Y*π*x (3).
Luego, plantea la expresión de la función derivada segunda, y queda:
L ' ' = - 8*Y + (1/2)*Y*π = Y*(-8 + π/2) ≅ -6,4292*Y < 0,
y observa que la función derivada segunda es constante y negativa, por lo que la gráfica de la función es cóncava hacia abajo en todos sus puntos.
Luego, plantea la condición de punto crítico (posible máximo o posible mínimo):
L ' = 0, sustituyes la expresión señalada (3), y queda:
16*Y - 8*Y*x + (1/2)*Y*π*x = 0,
multiplicas en todos los términos de la ecuación por 2/Y, y queda:
32 - 16*x + π*x = 0,
haces pasaje de término, y queda:
- 16*x + π*x = - 32,
multiplicas en todos los términos de la ecuación por -1, y queda:
16*x - π*x = 32,
extraes factor común en el primer miembro, y queda:
(16 - π)*x = 32,
haces pasaje de factor como divisor, y queda:
x = 32/(16 - π) ≅ 2,4886;
luego, sustituyes en la expresión señalada (2), y queda:
y = 4 - 32/(16 - π) ≅ 1,5114.
Luego, reemplazas en las expresiones del ancho y del largo de la ventana rectangular, y en la expresión del radio del semicírculo, y tienes las dimensiones de la ventana completa
Espero haberte ayudado.
-
hola gente de unicoos, tengo una duda. tengo un ejercicio, me dice utilizar el polinomio de Mc Laurin de orden 4 para aproximar e1/4 Y estimar el error cometido,
ahora la duda mia es como calcular el error D: siempre me quivoco en esa parte
chado
el 20/10/17Antonius Benedictus
el 20/10/17 -
-
Dos botellas con la misma capacidad están llenas de una disolución de ácido en agua. Las razones del volumen de agua respecto al volumen de ácido son, respectivamente, 2: 1 y 4: 1. Abocamos el contenido de estas dos botellas en una garrafa muy grande. ¿Cuál será la razón del volumen de agua respecto del volumen de ácido en esta garrafa?
Gracias de antemano!Mar Lobato Espejo
el 20/10/17Antonio Silvio Palmitano
el 20/10/17Vamos con una precisión.
Indicamos con C a las cantidades de ácido en las botellas 1 y 2, con A a las cantidades de agua, e indicamos con x al volumen de cada botella.
Luego, tienes:
Botella 1:
tienes en total tres partes,
dos partes de agua: A1 = (2/3)x,
una parte de ácido: C1 = (1/3)x.
Botella 2:
tienes en total cinco partes,
cuatro partes de agua: A2 = (4/5)x,
una partes de ácido: C2 = (1/5)x.
Luego, cuando vuelcas todo en la garrafa, tienes:
Volumen total de agua:
AT = A1 + A2 = (2/3)x + (4/5)x = (2/3 + 4/5)x = (22/15)x.
Volumen total de ácido:
CT = C1 + C2 = (1/3)x + (1/5)x = (1/3 + 1/5)x = (8/15)x.
Luego, tienes para el volumen total de agua con respecto al volumen total de ácido:
AT/CT = (22/15)x / ( (8/15)x ) = simplificas = 22/8 = 11/4.
Espero haberte ayudado.
-
-
Ángel
el 20/10/17Ali Hussain
el 21/10/17 -
Cristian - hace 20 horas, 19 minutosHola Buenas Noche Unicoos ! Podríais ayudarme con el resto del ejercicio y decirme si lo que he echo esta bien por favor? Muchas gracias.