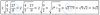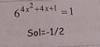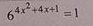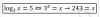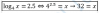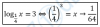-
Radicales:
Simplifica
2·√4/3·√27/8 como lo hago?
Ángel
el 9/10/17Laura Viñuela
el 9/10/17Ángel
el 9/10/17Laura Viñuela
el 9/10/17 -
Hola, como se resuelve este ejercicio:
Determina el valor de m que hace que se cumpla la condición indicada:
La inecuacion ((mx-5)/(2x+1))≤1 tiene como solución x perteneciente al intervalo (-1/2, 4).
Este ejercicio lo intentado resolver pero el menos un medio no está incluido porque hace 0 el denominador. Y luego cogiendo valores desde más un medio al 4 me van variando los valores de m.
¿Cómo se resolvería?
aliendo las soluciones
-
Ángel
el 9/10/17 -
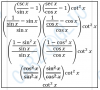
Hola, necesitaria como hacer los siguientes ejercicios. Estoy en bach a distancia y con los apuntes que me dan no consigo hacer nada.

Antonio Silvio Palmitano
el 9/10/17Observa que tanto el numerador como el denominador tienden a cero, por lo que el limite es indeterminado.
Luego, factorizas (observa que tanto el numerador como el denominador son expresiones polinómicas cuadráticas) por medio de la fórmula de Baskara (o si prefieres, con la Regla de Ruffini empleando la raíz x = -3), y queda:
Lím(x→-3) 2*(x+3)*(x+3) / ( (x+3)*(x-2) ) = simplificas = Lím(x→-3) 2*(x+3)/(x-2) = resuelves = 2*(-3+3)/(-5) = 2*0/(-5) = 0.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 9/10/17Observa que puedes expresar el factor integral en el argumento del límite, y éste queda:
(1/h) * (3-h)∫(3+h) f(x)*dx = (1/h) * (3-h)∫3 f(x)*dx + (1/h) * 3∫(3+h) f(x)*dx =
luego, plantea la regla de Barrow para cada integral (observa que llamamos F a la primitiva de la función f):
= (1/h) * ( F(3) - F(3-h) ) + (1/h) * ( F(3+h) - F(3) ) =
luego, plantea la sustitución (cambio de variable) t = - h (observa que t tiende a 0 cuando h tiende a 0), y queda:
= - (1/t) * ( F(3) - F(3+t) ) + (1/h) * ( F(3+h) - F(3) ) =
extraes factor común -1 en el segundo factor del primer término, resuelves signos en dicho término, y queda:
= (1/t) * ( -F(3) + F(3+t) ) + (1/h) * ( F(3+h) - F(3) ) =
aplicas la propiedad conmutativa de la suma en el segundo factor del primer término, y queda:
= (1/t) * ( F(3+t) + F(3) ) + (1/h) * ( F(3+h) - F(3) ).
Luego, tienes el límite en tu enunciado:
Lím(h→0) (1/h) * (3-h)∫(3+h) f(x)*dx =
sustituyes (recuerda que t tiende a 0 cuando h tiende a 0), y queda:
= Lím(t→0) (1/t) * ( F(3+t) + F(3) ) + Lím(h→0) (1/h) * (1/h) * ( F(3+h) - F(3) ) =
resuelves los productos en los argumentos de los límites, y queda:
= Lím(t→0) ( F(3+t) + F(3) )/t + Lím(h→0) (1/h) * ( F(3+h) - F(3) )/h =
observa que en ambos términos tienes la expresión de la derivada por definición de la función F, por lo tanto queda:
= F ' (3) + F ' (3) =
= 2 * F ' (3) =
aplicas el Teorema Fundamental del Cálculo Integral (recuerda que F es la función primitiva de f), y queda:
= 2 * f(3).
Espero haberte ayudado.