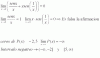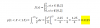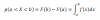-
Flor
el 5/10/17 -
Flor
el 5/10/17 -
fabian
el 5/10/17
Hola estoy confundido con este ejercicio yo pienso que se puede resolver con (1) y (2) es decir ambas juntas pero no estoy seguro
Se puede determinar las edades actuales de A y B si:
(1) A tiene el doble de la edad que B
(2) Hace 10 años A tenia el cuadruplo de la edad de B
A) (1) por si sola (es decir basta solo (1) para resolverla)
B) (2) por si sola (es decir basta solo (2) para resolverla)
C) Ambas juntas (1) y (2)
D) Cada una por si sola (1) o (2)
E) se requiere información adicional
Lo que he planteado
A = 2B
A-10= 4(B-10)
-
Roxana Hidalgo Romero
el 5/10/17Hola. En un cuestionario de clase me han echo esta pregunta
Si la massa de la Tierra és 5,98·1024 Kg y la del Sol és 1,98·1030 Kg.
¿Cual de las dos magnitudes es mas grande?
¿Cuantas veces es más grande?
Gracias
Ángel
el 5/10/17Si la massa de la Tierra és 5,98·1024 Kg y la del Sol és 1,98·1030 Kg.
¿Cual de las dos magnitudes es mas grande?
Tienes que fijarte en las potencias:
1,98·1030 Kg -------> Se trata de un número de 31 dígitos
5,98·1024 Kg --------> Se trata de un número de 25 dígitos
Como 31>25, entonces 1,98·1030 Kg es la magnitud más grande.
--------------------------------------------------------
¿Cuantas veces es más grande?
Tienes que dividir la magnitud mayor entre la menor:
(1,98·1030)÷(5,98·1024)=
(19,8·1029)÷(5,98·1024)=
(19,8÷5,98)*1029-24=
3,31*105 veces más grande la masa del Sol que la de la Tierra.
-
Usuario eliminado
el 5/10/17Hola tengo una duda con la cuota de mensualidad, lo he intentado de mil maneras y no me sale. Por favor ayuda.
Se fija en uno de 60 metros cuadrados en primera línea de la playa un apartamento por 50.000€, para comprarlo solicita un préstamo con un interés fijo del 2% anual para devolverlo en 15 años mediante pagos mensuales. Hallar la cuota mensual que tiene que pa
-
Leticia
el 5/10/17me podrian decir como se resuelve un logaritmo
Ángel
el 5/10/17https://www.unicoos.com/video/matematicas/4-eso/ecuaciones-y-sistemas/logaritmos/logaritmos-01
https://www.unicoos.com/video/matematicas/4-eso/ecuaciones-y-sistemas/logaritmos/logaritmos-02
https://www.unicoos.com/video/matematicas/4-eso/ecuaciones-y-sistemas/logaritmos/logaritmos-03
https://www.unicoos.com/video/matematicas/4-eso/ecuaciones-y-sistemas/logaritmos/logaritmos-04
-
Jose
el 5/10/17 -
Jesús
el 5/10/17La función por si no se ve es :
0 si x < 0
f(x): x/2 si 0≤x≤2
0 si x>2
Probabilidad de : (1<ξ<1'5),
Antonio Silvio Palmitano
el 5/10/17Puedes plantear para la función de distribución acumulada:
F(x) =
0 si x < 0
0∫x (u/2)*du si 0 ≤ x ≤ 2
1 si x > 2;
resuelves la integral en el segundo trozo, y queda:
F(x) =
0 si x < 0
x2/4 si 0 ≤ x ≤ 2
1 si x > 2.
Luego, tienes:
p( ξ ≤ 1,2 ) = F(1,2) = 1,22/4 = 1,44/4 = 0,36.
p( 1 < ξ 1,5 ) = F(1,5) - F(1) = 1,52/4 - 12/4 = 2,25/4 - 1/4 = 1,25/4 = 0,3125.
Espero haberte ayudado.
-
Jesús
el 5/10/17Hola,buenos días, alguien me podría ayudar con este ejercicio miren:
Este es el ejercio y pude hacer el primer aprtado , pero el segundo soy incapaz , es este :
Este ejercicio por probabilidad me da : 0'3125
Pero por integrales , estoy atascado ,porque, empiezo en la integral desde menos infinito a cero y esa se que vale cero, pero despues para hacer lo que serian las integrales de la F(1'5)-F(1) ahi ya no se como hacer , si poner integral desde cero a 1'5 menos la integal desde 1'5 a 1 o si poner integral desde cero a 1.
Muchas gracias, cualquier sugerencia meserá de mucha ayuda.
-
Andres Sampayo
el 5/10/17
, Alguien me podria ayudar con este ejercicio, llevo 3 semanas
intentandolo hacer y no logro pasar del analisis, por favor que es
urgente, necesito ayuda, asi sea nada mas la parte A
Antonio Silvio Palmitano
el 5/10/17Considera un punto genérico de la elipse: P(x,y,z).
A partir de la ecuación del cilindro, puedes plantear la expresión de la ordenada en función de la abscisa:
y = √(9-x2) (1)
En la ecuación del plano tienes la expresión de la coordenada z del punto P, y con la expresión anterior tienes:
z = 2x + 3y = 2x + 3√(9-x2) (2).
Luego, plantea la expresión del vector OP, que está incluido en el plano que lo contiene a él y al eje OZ:
OP = < x , y , z > = < x , √(9-x2) , 2x + 3√(9-x2) >.
Luego, con el vector característico del eje OZ (< 0 , 0 , 1 >) y el vector OP, puedes plantear su producto vectorial y tienes una expresión del vector normal del plano que los contiene:
n1 = < 0 , 0 , 1 > x < x , y , z > = < x , √(9-x2) , 2x + 3√(9-x2) > = < -√(9-x2) , x , 0 >,
cuyo módulo queda:
|n1| = √( ( -√(9-x2) )2 + x2 + 02 ) = √(9 - x2 + x2) = √(9) = 3.
Luego, plantea la expresión del vector unitario característico del plano OXZ: j = < 0 , 1 , 0 >.
Luego, a partir de la expresión de su producto escalar, plantea la expresión del coseno del ángulo determinado por los vectores n1 y j, y tienes:
cosθ = n1 • j / (|n1|*|j|) = < -√(9-x2) , x , 0 > • < 0 , 1 , 0 > / (3*1) = x/3;
luego, despejas y tienes la expresión de la primera componente del vector genérico OP:
x = 3*cosθ;
luego, sustituyes en la expresión señalada (1) y tienes para la segunda componente del vector genérico OP:
y = √( 9 - (3*cosθ)2 ) = √(9 - 9*cos2θ) = √( 9*(1 - cos2θ) ) = √(9*sen2θ) = 3*senθ;
luego, sustituyes en la expresión señalada (2) y tienes para la tercera componente del vector genérico OP:
z = 2*3*cosθ + 3*3*senθ = 6*cosθ + 9*senθ.
Luego, tienes las tres componentes del vector posición: OP = R(θ), cuya expresión queda:
R(θ) = < 3*cosθ , 3*senθ , 6*cosθ + 9*senθ >.
Luego, derivas con respecto al tiempo (observa que debes emplear la regla de la cadena) y queda:
v(θ) = dR/dt = < -3*senθ*dθ/dt , 3*cosθ*dθ/dt , (-6*senθ + 9*cosθ)*dθ/dt >, extraes el factor común escalar, y queda:
v(θ) = dθ/dt*< -3*senθ , 3*cosθ , -6*senθ + 9*cosθ >, sustituyes la expresión de la derivada del ángulo, y queda:
v(θ) = ω*< -3*senθ , 3*cosθ , -6*senθ + 9*cosθ >.
Luego, derivas con respecto al tiempo (observa que debes emplear la regla de la cadena) y queda:
a(θ) = dv/dt = ω*< -3*cosθ*dθ/dt , -3*senθ*dθ/dt , (-6*cosθ - 9*senθ)*dθ/dt >, extraes el factor común escalar, y queda:
a(θ) = ω*dθ/dt*< -3*cosθ , -3*senθ , -6*cosθ - 9*senθ >, sustituyes la expresión de la derivada del ángulo, y queda:
a(θ) = ω2*< -3*cosθ , -3*senθ , -6*cosθ - 9*senθ >.
Espero haberte ayudado.
