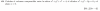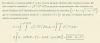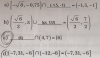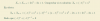-
 sabiendo que log en base a de b=4 ; log en base b de a= 1/4 y log en base a de c=-3 como se haría esto?
sabiendo que log en base a de b=4 ; log en base b de a= 1/4 y log en base a de c=-3 como se haría esto?Antonio Silvio Palmitano
el 2/10/17Tienes los datos
loga(b) = 4, aplicas la definición de logaritmo, y tienes b = a4;
logb(a) = 1/4, aplicas la definición de logaritmo, y tienes: a = b1/4;
loga(c) = -3, aplicas la definición de logaritmo, y tienes: c = a-3.
Luego, plantea la expresión de la base del logaritmo del enunciado:
√(a*b) = √(a*a4) = √(a5) = a5/2.
Luego, plantea la expresión del argumento del logaritmo del enunciado:
a2*c = a2*a-3 = a-1.
Luego, plantea para el logaritmo de tu enunciado
log√(a*b) (a2*c) = sustituyes = loga^5/2 (a-1) = x;
luego, aplica la definición de logaritmo para la última igualdad, y queda
a-1 = (a5/2)x, aplicas la propiedad de la potencia cuya base es otra potencia en el segundo miembro, y queda:
a-1 = a(5/2)*x, luego, por igualdad entre potencias con bases iguales, igualas exponentes, y queda
-1 = (5/2)*x, multiplicas en ambos miembros por 2/5 y queda:
-2/5 = x.
Espero haberte ayudado.
-
Hola chicos, una ayuda con este ejercicio?
cos(2α) = 1 - sen²(α)
Tengo que demostrar esa igualdad. Yo lo que hice fue esto:
cos(α + α) = cos(α).cos(α) - sen(α).sen(α)
cos(α + α) = cos²(α) - sen²(α)
Y ya no se como seguir.. no entiendo de donde es que sale el 1- ni como llegar a eso.
Gracias :)
Ángel
el 2/10/17Tenemos en tu enunciado que:
cos(2a) = 1 - sen2a
Por definición del ángulo doble tenemos la fórmula:
cos(2a)= cos2a - sen2a
Entonces hay que demostrar que:
1 - sen2a = cos2a - sen2a -------------> 1
- sen2a= cos2a- sen2a-----------> cos2a = 1 --------> cos a= ±1-------> a1=arccos(1) = 0º + 360K ------> a2= arccos(-1)= 180º + 360K
Gekka
el 2/10/17Hola Angel, gracias por tu ayuda :)
Esta bien lo que hiciste pero el ejercicio lo que me pide, quizás me explique mal, es que demuestre como cos(2α) se "transforma" en 1 - sen²(α)
No se si me explico bien..
Pero, utilizando propiedades trigonométricas tengo que llegar de cos(2α) a -----> 1 - sen²(α)
Ángel
el 2/10/17cos(2α) = 1 - sen²(α)
cos(2α)= cos(α + α) = cos(α).cos(α) - sen(α).sen(α) = cos²(α) - sen²(α) = 1-sen²(α) - sen²(α) = 1 -2sen2a
Planteamos para que valores de a se se cumple que cos(2a)= 1 - sen²(α) = 1 -2sen2a
1 - sen²(α) = 1 -2sen2a --------> -sen2a= 0 --------> sen a = 0 --------> arcsen (0)= 0º +180K (que es la misma solución que obtuvimos de la otra forma)
-
Hola Unicoos.
Una ayuda con este ejercicio.
Calcula el valor de m y n para que las rectas r y s sean perpendiculares y el punto A(-2,7) pertenezca a la recta r.
s:3x+ny+8=0
Gracias ,sois unos máquinas.
Desencadenado
el 2/10/17La teoría dice que para ser perpendicular, la pendiente debe ser de signo contrario e inversa multiplicativa, por ejemplo;
2/3× la perpendicular sería -3/2×
En el ejercicio tu pendiente es 3× entonces le cambio el signo -3× y la invierto -1/3×
Espero lo entiendas.
Saludos!!!
-
 Hola unicoos. Necesito ayuda con esta integral, por más que lo intento no me sale. Llego a este resultado: 8/3*(1-cos^3(θ)), que está mal.
Hola unicoos. Necesito ayuda con esta integral, por más que lo intento no me sale. Llego a este resultado: 8/3*(1-cos^3(θ)), que está mal.Fermat
el 2/10/17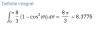
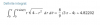 Hola Javier, si te fijas en mi pregunta, me salió el mismo resultado que a ti, que en un principio pensé que era correcto. Sin embargo al comprobarlo con un programa me di cuenta de que no estaba bien. El ejercicio se trata de hacer integrales iteradas y es este paso el que me produce el error. Te adjunto unas capturas para que entiendas mejor lo que quiero transmitirte. Muchas gracias.
Hola Javier, si te fijas en mi pregunta, me salió el mismo resultado que a ti, que en un principio pensé que era correcto. Sin embargo al comprobarlo con un programa me di cuenta de que no estaba bien. El ejercicio se trata de hacer integrales iteradas y es este paso el que me produce el error. Te adjunto unas capturas para que entiendas mejor lo que quiero transmitirte. Muchas gracias.Fermat
el 2/10/17Fermat
el 2/10/17Antonius Benedictus
el 2/10/17Fermat
el 2/10/17Fermat
el 2/10/17 -
Antonio Silvio Palmitano
el 2/10/17Van los intervalos que faltan consignar.
a)
Observa que el intervalo solución está incluido en el primer intervalo, por lo tanto completa con: ( -1,5 ; -1 ].
b)
Observa que el primer intervalo está incluido en el intervalo solución, por lo tanto completa con: [ π ; 7/2 ).
c)
Observa que el conjunto unitario solución está incluido en el segundo intervalo, por lo tanto completa con: { 6 }.
d)
Observa que el intervalo solución está incluido en el segundo intervalo, por lo tanto completa con: ( -7,31 ; -6 ].
Espero haberte ayudado.