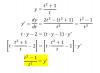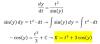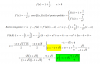Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

Paula
el 1/10/17

Hola como hago la comprobación de la solución y=(t^2+1)/t de la ecuación diferencial ty -2 =(ty-1)y'

••0 voto/s
•
Axel Morales Piñón.
el 1/10/17
Así Paula:

•1 voto/s
•

Cancelar
Paula
el 1/10/17

Hola, ayuda con estas ecuaciones diferenciales por él método de variable separable por favor

••0 voto/s
•
Axel Morales Piñón.
el 1/10/17

•2 voto/s
•
jorge velazquez
el 1/10/17
y'=t/y^2
Cambiar y'=dy/dt
dy/dt=t/y^2
Paso previo
dy=(dy/dt)dt para conseguir el diferencial

(y^2)dy=tdt
Integramos
Int(y^2)dy=int(t)DT
y^3/3=t^2/2 +c
común denominado
Y^3/3=[ (t^2) + 2c]/2
y^3=(3t^2+ 6c)/2
CambIamos 6c=K
y(1)=1
1^3=(3(1)^2+k)/2
Despejamos
2=3+k
K=-1

•2 voto/s
•

Cancelar
Jonathan Yañez
el 1/10/17

En un sencillo juego de vídeo unos aviones vuelan de izquierda a derecha siguiendo la
trayectoria de y=1+1/x, x>0. Pueden disparar proyectiles en la dirección de la tangente
a la curva. Si hay un objetivo en el punto P=(4;0), ¿donde se debe hacer el disparo para
acertar en el blanco?

Adelanto que la rta es: P=(√5-1; (5+√5)/4)

••0 voto/s
•
Antonius Benedictus
el 1/10/17

•1 voto/s
•
Jonathan Yañez
el 4/10/17
gracias!!

•0 voto/s
•

Cancelar
Ingrid
el 1/10/17

me ayudan , con este ejercicio:
Muchas gracias

••0 voto/s
•
Antonius Benedictus
el 1/10/17

•1 voto/s
•

Cancelar
Andrea H. Formentí
el 1/10/17

Hola, de nuevo ..:) Por que 24 -2K ≠ 0 es N/0 ? ; hayamos a la vez que K=12
K es el valor que busco para que f(x) tenga limite finito en x=-3
f(x) = x^2-5x-2K / x+3

••0 voto/s
•
Antonius Benedictus
el 1/10/17
Si no pones foto del enunciado original, no nos podemos aclarar.

•0 voto/s
•
Antonio Silvio Palmitano
el 1/10/17
Si la expresión de la función es:
f(x) = (x² - 5*x - 2*k)/(x + 3),
observa que el denominador tiende a cero cuando x tiende a - 3, por lo que es condición necesaria que el numerador también tienda a cero para que exista el límite.
Luego, plantea el límite para x tendiendo a - 3 del numerador:
Lím(x→-3) (x² - 5*x - 2*k) = (-3)2 - 5*(-3) - 2*k = 9 + 15 - 2*k = 24 - 2*k = 0,
luego, despejas en la última igualdad remarcada, y queda: k = 12.
Luego, reemplazas en la expresión del numerador, y queda:
N = x² - 5*x - 2*12 = x² - 5*x - 24 = factorizas = (x + 3)*(x - 8).
Luego, plantea el límite que te piden en el enunciado:
Lím(x→-3) (x² - 5*x - 24/(x + 3) = sustituyes en el numerador = Lím(x→-3) (x + 3)*(x + 8)/(x + 3) = simplificas = Lím(x→-3) (x + 8) = - 3 + 8 = 5.
Espero haberte ayudado.

•1 voto/s
•

Cancelar
Ingrid
el 1/10/17

Me podrían ayudar con este ejercicio, por favor

••0 voto/s
•
Antonius Benedictus
el 1/10/17

•1 voto/s
•

Cancelar
Andrea H. Formentí
el 1/10/17

Bien, perdonad que este del revés, este es un ejercicio que puso mi profe como ejemplo de teoria la cosa es que a él le daba 1 que venía de e^0. Como yo lo he vuelto ha hacer porque mi profe pues se salta bastantes pasos y ahora que lo he hecho yo veo que no me da lo mismo, podriais decirme en donde me he equivocado? Gracias :*

••0 voto/s
•
Antonius Benedictus
el 1/10/17
Andrea, tienes mal hecha la resta de fracciones. El denominador no es 1, es x^2.

•0 voto/s
•

Cancelar
Jose antonio
el 1/10/17

Hola a ver quien me puede ayudar con este ejercicio.

••0 voto/s
•
Usuario eliminado
el 1/10/17
solo pone eso en el ejercicio ???

•0 voto/s
•
Antonius Benedictus
el 1/10/17

•0 voto/s
•

Cancelar
Miriam
el 1/10/17

hola tengo una duda a ver si vosotros podeis resolvérmela...... como se calcula esta potencia
5⁰: 5^-4partido de 5^-1· 5 ⁸
gracias de antemano

••0 voto/s
•
Antonio Silvio Palmitano
el 1/10/17
Vamos por separado:
5⁰ : 5^-4 = 5^0-(-4) = 5⁰⁺⁴ = 5⁴;
5^-1*5⁸ = 5^-1+8 = 5⁷.
Luego, plantea la expresión de tu enunciado:
(5⁰ : 5^-4) / (5^-1*5⁸) = reemplazas = 5⁴ / 5⁷ = 5^4-7= 5^-3.
Espero haberte ayudado.

•1 voto/s
•
Miriam
el 2/10/17
gracias

•0 voto/s
•

Cancelar
Santi
el 1/10/17

Alguien podría explicarme como hacer esto?

••0 voto/s
•
Ángel
el 1/10/17
Si x<y, entonces y=x+ε
Entonces (x+y)/2 = (x+x+ε)/2 = x + ε/2
Por lo que x<y →    x< x + ε/2 < x+ε
Concluimos que la media aritmética se encuentra entre x e y

•0 voto/s
•
Antonius Benedictus
el 1/10/17

•0 voto/s
•
Usuario eliminado
el 1/10/17
hola antonio y angel, yo tambien tengo problema en este ejercicio y nuestro problema es que lo tenemos que justificar con palabras y no sabes como, si nos podriais ayudar seria un gran favor gracia

•0 voto/s
•
Santi
el 1/10/17
gracias por la ayuda, me gustaría que me ayudarais a justificarlo con palabras el ejercicio

•0 voto/s
•
Ángel
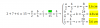
el 1/10/17
Si x<y, entonces y=x+ε    ---------------------------->    "Si x es menor que y entonces y=x+algo"
Entonces (x+y)/2 = (x+x+ε)/2 = x + ε/2   ----------------------------> "Como y= x+algo, entonces  (x+y)/2 = (x+x+algo)/2 = x + algo/2
Por lo que x →    x< x + ε/2 < x+ε ----------------------------> "Por lo que x es menor que y, verifica que x es menor que x más la mitad de algo, y este es menor que x más algo
Concluimos que la media aritmética se encuentra entre x e y

**Con "algo" nos referimos a un trozo, muy pequeño o muy grande, pero siempre mayor que cero. Lo hemos representado con el letra griega épsilon ε

•1 voto/s
•
Usuario eliminado
el 1/10/17
Muchas gracias Angel, tengo el mismo problema que santi, pero yo no logro entenderlo y me hace mas dificil entenderlo con palabras, pero muchas gracias por ayudarme pero me gustaria especificarlo ya que e dicho que tengo que solucionarlo con palabras

•0 voto/s
•
Usuario eliminado
el 1/10/17
¿ Antonio también podrías ayudarnos ? a justificarlo con palabras, gracias.

•0 voto/s
•

Cancelar