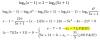-
Hola, necesito ayuda con el siguiente problema. Gracias de antemano.
2. Sea y una función de x definida implícitamente por la curva de ecuación 2(x^2 + y^2 )^2 = 25(y^2 − x^2 ).Determine la pendiente de la recta tangente a la curva y = f(x) en el punto (1, 3).
Antonio Silvio Palmitano
el 2/10/17Comienza por derivar implícitamente con respecto a x:
4*(x2 + y2)*( 2x + 2*y*y ' ) = 25*( 2*y*y ' - 2*x).
Luego, reemplazas las coordenadas del punto en estudio (1,3), y queda:
4*(1 + 9)*( 2 + 6*y ' ) = 25*( 6*y ' - 2 ),
resuelves coeficientes, distribuyes, y queda:
80 + 240*y ' = 150*y ' - 50,
haces pasajes de términos, y queda:
90*y ' = -130,
haces pasaje de factor como divisor, y queda:
y ' = - 13/9, que es el valor de la pendiente de la recta tangente a la curva en el punto (1,3).
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 2/10/17Observa que la longitud de la base del triángulo queda expresada:
b = x - 2.
Observa que la altura del triángulo queda expresada:
h = f(x).
Luego, plantea la expresión del área del triángulo:
A = (1/2)*b*h,
sustituyes expresiones, y queda:
A = (1/2)*(x-2)*f(x).
Luego, plantea la expresión de la derivada primera de la función área (observa que debes aplicar la regla del producto):
A ' = (1/2)*f(x) + (1/2)*(x-2)*f ' (x).
Luego, plantea la condición de punto crítico (posible máximo o posible mínimo):
A ' = 0,
sustituyes la expresión de la derivada en el primer miembro, y queda:
(1/2)*f(x) + (1/2)*(x-2)*f ' (x) = 0,
multiplicas por 2 en todos los términos de la ecuación, y queda:
f(x) + (x - 2)*f ' (x) = 0 (1).
Luego, tienes la expresión de la función en tu enunciado:
f(x) = e-2*(x-2)^2,
luego, plantea la expresión de su función derivada:
f ' (x) = -4*(x-2)*e-2*(x-2)^2;
luego, sustituyes ambas expresiones en la ecuación señalada (1) y queda:
e-2*(x-2)^2 - 4*(x - 2)2*e-2*(x-2)^2 = 0;
divides en todos los términos de la ecuación por el factor exponencial (observa que es estrictamente positivo), y queda:
1 - 4*(x - 2)2 = 0,
haces pasaje de término, y queda:
- 4*(x - 2)2 = - 1,
haces pasaje de factor como divisor, y queda:
(x - 2)2 = 1/4,
haces pasaje de potencia como raíz, y tienes dos opciones:
a)
x - 2 = -1/2, haces pasaje de término, y queda:
x = 3/2, que no pertenece al intervalo [2,5];
b)
x - 2 = 1/2, haces pasaje de término, y queda:
x = 5/2, que si pertenece al intervalo [2,5];
luego, evalúas en la expresión de la función, y queda:
f(5/2) = e-2*(1/2)^2 = e-1/2;
luego, reemplazas valores en la expresión remarcada del área del triángulo, y queda:
A = (1/2)*(5/2 - 2)*e-1/2 = (1/4)*e-1/2.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 1/10/17Plantea la expresión del número complejo en forma cartesiana binómica: z = x + y*i (observa que designamos con x a la parte real, y con y a la parte imaginaria del número).
Plantea la expresión del número complejo conjugado: zc = x - y*i.
a)
Plantea la suma del número con su conjugado:
z + zc = x + y*i + x - y*i = reduces términos semejantes (observa que tienes cancelaciones) = 2*x;
luego, con el primero y con el último miembro de la cadena de igualdades tienes la ecuación:
z + zc = 2*x, haces pasaje de factor como divisor, y queda:
(z + zc)/2 = x = Re(z).
b)
Plantea la resta del número con su conjugado:
z - zc = x + y*i - (x - y*i) = distribuyes el agrupamiento = x + y*i - x + y*i = reduces términos semejantes (observa que tienes cancelaciones) = 2*y*i;
luego, con el primero y con el último miembro de la cadena de igualdades tienes la ecuación:
z - zc = 2*y*i, haces pasaje de factores como divisores, y queda:
(z + zc)/(2*i) = y = Im(z).
Espero haberte ayudado.
-
Antonio
el 1/10/17
como 3 = log663
entonces
3 - log6(5x+1) = log663- log6(5x+1) = log6 [63-(5x+1)] = log6 (63-5x-1)
por lo tanto
log6(x-1) = 3 - log6(5x+1) => log6(x-1) = log6 (63-5x-1) => x-1 = 63-5x-1
y resolviendo la ecuación de primer grado
x-1 = 63-5x-1 => x+5x = 63-1+1 => 6x = 63 => x= 62
-
Hola!, me podrian ayudar con el siguiente limite:
lim cuando n tiende a infinito ((-1)^n)/(n^2)
Gracias!Antonio Silvio Palmitano
el 1/10/17Observa que tienes la expresión:
an = (-1)n/n2.
Luego, plantea su valor absoluto:
An = |an| = |(-1)n/n2| = 1/n2.
Luego, plantea el límite de esta última expresión:
Lím(n→∞) An = Lím(n→∞) (1/n2) = 0,
por lo que puedes concluir:
Lím(n→∞) an = Lím(n→∞) ( (-1)n/n2) = 0.
Recuerda que si el límite para n tendiendo a infinito del valor absoluto de la expresión es igual a cero, entonces el límite de la expresión también lo es.
Espero haberte ayudado.
-
Alguien conoce como resolver el sig problema de geometria analitica?: "Halla la ecuacion de la recta cuya ordenada al origen es igual a -3 y que es perpendicular a la rceta: x-3y+8=0"?por favor me urge...
Antonio Silvio Palmitano
el 1/10/17Tienes la ecuación cartesiana implícita de la recta dato:
x - 3y + 8 = 0, haces pasajes de términos y queda:
- 3y = - x - 8, divides en todos los términos de la ecuación por -3 y queda:
y = (1/3)*x + 8/3, que es la ecuación cartesiana explícita de la recta dato.
Luego, observa que su pendiente es: m = 1/3 y, por la condición de perpendicularidad, tienes que la pendiente de la recta buscada es: m1 = -1/(1/3) = - 3,
luego, con la ordenada al origen que tienes en el enunciado, tienes que la ecuación cartesiana explícita de la recta buscada es:
y = - 3x - 3.
Espero haberte ayudado.
-
 chicxs me puedes ayudar cn esta duda existencial tengo poquito tiempo besitos
chicxs me puedes ayudar cn esta duda existencial tengo poquito tiempo besitos Ángel
el 1/10/17Mira la pregunta de ani01 https://www.unicoos.com/foro/matematicas/page:3 , ahí la tienes contestada.
-
Hola soy nueva en unicoos tengo el paquete premium, pero no se donde puedo ver los ejercicios resueltos y todo lo que puedo acceder con este paquete.
MUCHISIMAS GRACIAS
-
Antonio Silvio Palmitano
el 1/10/17Puedes plantear la ecuación cartesiana explícita de la recta:
y = a*x + b.
Luego, para determinar su abscisa al origen, reemplazas y = 0 en la ecuación, y queda:
0 = a*x + b, haces pasaje de término, y queda:
-a*x = b, haces pasaje de factor como divisor, y queda:
x = - b/a, por lo que la recta corta al eje coordenado OX en el punto: A(-b/a,0), y observa que -b/a debe ser estrictamente positivo.
Luego, para determinar su ordenada al origen, reemplazas x = 0 en la ecuación, y queda:
y = a*0 + b, resuelves y queda:
y = b, por lo que la recta corta al eje coordenado OY en el punto: B(0,b), y observa que b debe ser estrictamente positivo.
Luego, plantea para el área del triángulo rectángulo del primer cuadrante, con vértices AOB, con ángulo recto en el vértice O(0,0):
A = (1/2)*(-b/a)*b, resuelves productos y queda:
A = - (1/2)*b2/a. (1).
Luego, como el punto (5,5) pertenece a la recta, reemplazas sus coordenadas en su ecuación, y queda:
5 = a*5 + b, haces pasaje de término, y queda:
5 - 5*a = b, extraes factor común, y queda:
5*(1 - a) = b (2).
Luego, sustituyes la expresión señalada (2) en la ecuación señalada (1), y queda:
A = - (1/2)*( 5*(1-a)/a )2/a, desarrollas el argumento del cuadrado, y queda:
A = - (1/2)*(25*(1 - 2*a + a2)/a), resuelves factores, distribuyes el divisor, y queda:
A = - (25/2)*( 1/a - 2 + a), que es la expresión del área del triángulo en función de la pendiente de la recta.
Luego, plantea la expresión de la función derivada:
A ' = - (25/2)*(-1/a2 + 1) (3),
luego, plantea la condición de punto crítico (posible máximo o posible mínimo:
A ' = 0, sustituyes la expresión señalada (3) y queda:
- (25/2)*(-1/a2 + 1) = 0, multiplicas por - 25/2 en ambos miembros de la ecuación, y queda:
-1/a2 +1 = 0, haces pasaje de término, y queda:
1 = 1/a2, haces pasaje de divisor como factor, y queda:
a2 = 1, haces pasaje de potencia como raíz, y tienes dos opciones:
1°)
a = -1, que es la pendiente de la recta, luego reemplazas en la ecuación señalada (2) y queda:
10 = b, que es la ordenada al origen, y corresponde al primer cuadrante,
luego, la abscisa al origen queda:
- b/a = - 10/(- 1) = 10, que corresponde al primer cuadrante,
por lo que la ecuación de la recta queda:
y = - x + 10.
2°)
a = 1, que es la pendiente de la recta, luego reemplazas en la ecuación señalada (2) y queda:
0 = b, que es la ordenada al origen,
luego la abscisa al origen queda:
- b/a = - 0/1 = 0,
por lo que la ecuación de la recta queda:
y = x, que no corresponde a este problema, porque no determina un triángulo con los ejes coordenados.
Espero haberte ayudado.