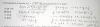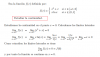-
Hola unicoos, no se como se esta realizando este ejercicio, por fa ayúdenme con el proceso mas fácil, gracias.
Antonio Silvio Palmitano
el 9/9/17Observa que puedes apelar a una representación gráfica.
Has completado bien el binomio elevado al cuadrado en el argumento de la raíz, luego puedes denominar y = f(x), y tienes:
y = √(-4*(x + 3/2)2 + 9), observa que y toma valores positivos (1), luego haces pasaje de raíz como potencia y queda:
y2 = -4*(x + 3/2)2 + 9, haces pasaje de término y queda:
4*(x + 3/2)2 + y2 = 9, divides por 9 en todos los términos de la ecuación y queda:
4*(x + 3/2)2 / 9 + y2 / 9 = 1, escribes el coeficiente en el numerador del primer término como divisor en su denominador, y queda:
(x + 3/2)2 / (9/4) + y2 / 9 = 1,
que es la ecuación canónica de una elipse, cuyos elementos son:
C(-3/2,0) (centro de simetría),
eje focal paralelo al eje OY: x = -3/2,
semieje mayor: a = 3,
semieje menor: b = 3/2,
vértices principales: A1(-3/2,3) y A2(-3/2,-3),
vértices secundarios (o covértices): B1(-3,0), B2(0,0).
Luego, puedes graficar la elipse (es muy útil que hagas el gráfico), y si tienes en cuenta la observación señalada (1) verás que debes considerar la semielipse superior.
Luego, observa que el vértice principal A1(-3/2,3) tienes su abscisa x = - 3/2 que pertenece al intervalo ]-2,0],
luego, si trazas tres rectas paralelas al eje OY cuyas ecuaciones son:
x = - 2, verás que corta a la elipse en el punto: P1(-2,√(8)),
x = - 3/2, verás que corta a la elipse en el vértice principal: A1(-3/2,3),
x = 0, verás que corta a la elipse en el vértice secundario: B2(0,0).
Luego, observa que tienes tres puntos que determinan un arco de la semielipse, limitada por los puntos:
P1(-2,√(8)), que no pertenece al arco de semielipse, ya que su abscisa x = - 2 no pertenece al intervalo ]-2,0],
B2(0,0), que si pertenece al arco de semielipse, ya que su abscisa x = 0 si pertenece al intervalo ]-2,0],
y tienes un punto intermedio:
A1(-3/2,3), que si pertenece al arco de semielipse (es un vértice principal), ya que su abscisa pertenece al intervalo ]-2,0]-
Luego, traza tres rectas paralelas al eje OX que pasen por los puntos que hemos indicado, y verás que la proyección del arco de semielipse sobre el eje OY
es un segmento, cuyos puntos límites son:
y = 0, punto limitante inferior, que es la proyección del punto B2(0,0),
y = 3, punto limitante superior, que es la proyección del punto A1(-3/2,3),
y observa que para el tercer punto tienes:
y = √(8), que es un punto intermedio del segmento determinado por la proyección del arco de semielipse sobre el eje OY.
Luego, tienes que la proyección del arco de semielipse sobre el eje OY determina el intervalo cerrado:
[0,3], que es la representación gráfica del recorrido de la función, cuya expresión tienes en tu enunciado.
Espero haberte ayudado.
-
Ángel
el 9/9/17Resolviendo el sistema de ecuaciones (en rojo) te queda que:
a= 5/6 - λ/12 b= (-λ+4)/3 c= λ
Antonio Silvio Palmitano
el 9/9/17Vamos por pasos.
1°)
Continuidad en x = -2 (observa que es un punto de corte entre trozos, por lo que empleamos la definición):
a)
f(-2) = observa que corresponde a la primera rama = 12/∛((-2)2+4) = 12/∛(8) = 12/2 = 6;
b)
Lím(x→-2-) f(x) = Lím(x→-2-) 12/∛(x2+4) = 6,
Lím(x→-2+) f(x) = Lím(x→-2+) (ax2 + bx + c) = 4a - 2b + c,
luego, como los límites laterales deben coincidir, tienes la ecuación:
4a - 2b + c = 6 (1).
2°)
Continuidad en x = 2 (observa que es un punto de corte entre trozos, por lo que empleamos la definición):
a)
f(2) = observa que corresponde a la primera rama = 12/∛((2)2+4) = 12/∛(8) = 12/2 = 6;
b)
Lím(x→2-) f(x) = Lím(x→2-) (ax2 + bx + c) = 4a + 2b + c,
Lím(x→2+) f(x) = Lím(x→2+) 12/∛(x2+4) = 6,
luego, como los límites laterales deben coincidir, tienes la ecuación:
4a + 2b + c = 6 (2).
3°)
Derivabilidad en x = -2:
comienza por plantear las expresiones de las derivadas para cada rama de la función:
a)
para la primera rama tienes:
f(x) = 12*(x2 + 4)-1/3, cuya derivada queda: f ' (x) = -4*(x2 + 4)-2/3*2x = -8x*(x2 + 4)-2/3;
luego, plantea el límite de la función derivada para x tendiendo a -2 por la izquierda:
Lím(x→-2-) f ' (x) = Lím(x→-2-) (-8x*(x2 + 4)-2/3) = 16/4 = 4;
b)
para la segunda rama tienes:
f(x) = ax2 + bx + c, cuya derivada queda: f ' (x) = 2ax + b;
luego, plantea el límite de la función derivada para x tendiendo a -2 por la derecha:
Lím(x→-2+) f ' (x) = Lím(x→-2+) (2ax + b) = - 4a + b;
c)
como debe cumplirse que la función derivada debe estar definida en x = -2, planteas la igualdad de las derivadas laterales y tienes la ecuación:
- 4a + b = 4 (3).
Luego, con las ecuaciones señaladas (1) (2) (3) tienes el sistema:
4a -2b + c = 6
4a + 2b + c = 6
- 4a + b = 4,
resuelves el sistema (te dejo la tarea) y su solución es:
a = - 1, b = 0, c = 10;
y observa que las derivadas laterales de la función para x = - 2 valen 4, por lo que puedes definir:
f ' (-2) = 4;
y observa que la función es continua en x = -2 y en x = 2, y que en ambos toma el valor 6.
Espero haberte ayudado.
-
Ayuda por favor ...
Sean las rectas perpendiculares:
L1: ax + (a+2)y - 6 = 0
L2: (2a - 1)x - ay + 1 = 0
Calcula el valor positivo que toma "a".
Ángel
el 9/9/17Antonio Silvio Palmitano
el 9/9/17Haces pasajes de términos en ambas ecuaciones y quedan:
(a+2)y = -ax + 6
-ay = -(2a-1)x - 1;
divides por a+2 en todos los términos de la primera ecuación (observa que damos por sentado que a+2 es distinto de 0);
divides por -a en todos los términos de la segunda ecuación (observa que damos por sentado que -a es distinto de 0),
y las ecuaciones quedan:
y = ( -a/(a+2) )x + 6/(a+2)
y = ( (2a-1)/a )x + 1/a;
por lo que tienes que las pendientes de las rectas quedan expresadas:
m1 = -a/(a+2),
m2 = (2a-1)/a.
Luego, puedes plantear la condición de perpendicularidad entre las dos rectas:
m2 = - 1/m1 (observa que damos por sentado que m1 es distinta de 0,
sustituyes expresiones, resuelves el segundo miembro (observa que tienes inversión y cambio de signo) y queda:
(2a-1)/a = (a+2)/a, multiplicas por a en ambos miembros de la ecuación (recuerda que damos por sentado que a es distinto de 0) y queda:
2a - 1 = a + 2, haces pasajes de términos y queda: a = 3.
Luego, reemplazas en las ecuaciones de las rectas y quedan:
L1: 3x + 5y - 6 = 0, cuya ecuación cartesiana explícita es: y = (-3/5)x + 6/5;
L2: 5x - 3y + 1 = 0, cuya ecuación cartesiana explícita es: y = (5/3)x + 1/3.
Espero haberte ayudado.
-
ayuda con esto: derivar : f(x)=(x)/(x+(c)/(x))
Ángel
el 9/9/17f(x)=(x)/(x+(c)/(x))
f(x)= x/ [x+(c/x)]
f´(x)= {1*[x+(c/x)] - x*[1+(-c/x2)}/[x+(c/x)]2
f´(x)= {x+(c/x) - x + (xc/x2)}/[x+(c/x)]2
f´(x)= {x+(c/x) - x + (c/x)}/[x+(c/x)]2
f´(x)= {(c/x) + (c/x)}/[x+(c/x)]2
f´(x)= (2c/x)/[x+(c/x)]2
f´(x)= (2c/x)/[(x2+c)/x]2
f´(x)= (2c/x)/[(x2+c)2/x2]
f´(x)= (2c*x2)/{x*[(x2+c)2]}
f´(x)= (2cx)/[(x2+c)2]
-
Guillem De La Calle Vicente
el 8/9/179. Primero debes saber que la pendiente de la recta que pasa por dos puntos, se calcula de la siguiente manera: m = (y1 - y2) / (x1 - x2) donde (x1,y1) y (x2, y2) son puntos de la recta. Para el problema tenemos los puntos:
A(-1,3)
B(5,1)
C(x,y)La pendiente del lado AC es siempre el doble que la del lado BC
(y - 3) / (x - (-1)) = 2 (y - 1) / (x - 5)
(y - 3) / (x +1) = 2 (y - 1) / (x - 5) ...resolvemos
(y - 3).(x - 5) = 2 (y - 1).(x +1)
xy -5y -3x +15 = 2xy +2y -2x -2
13 = xy + 7y + x
13 -x = xy + 7y
13 -x = y(x+7)
y = (13 -x) / (x+7)Antonio Silvio Palmitano
el 8/9/179a)
Plantea que el tercer vértice es el punto C(x,y).
Luego, plantea la pendiente del lado AC:
mAC = (y - 3)/(x + 1).
Luego, plantea la pendiente del lado BC:
mBC = (y - 1)/(x - 5).
Luego, tienes en tu enunciado que la relación entre las pendientes es:
mAC = 2*mBC,
sustituyes expresiones y queda:
(y - 3)/(x + 1) = 2*(y - 1)/(x - 5),
haces pasajes de divisores como factores y queda:
(x - 5)*(y - 3) = 2*(x + 1)*(y - 1),
distribuyes en ambos miembros y queda:
xy - 3x - 5y + 15 = 2xy - 2x + 2y - 2,
haces pasajes de términos y queda:
- xy - x - 7y + 17 = 0,
multiplicas en todos los términos de la ecuación por -1 y queda:
xy + x + 7y - 17 = 0.
9b)
Recuerda la identidad de la tangente del doble de un ángulo: tan(2α) = 2*tanα/(1-tan2α).
Luego, llama C(x,y) al tercer vértice, y observa que tienes (es muy conveniente que recurras a un gráfico):
Ángulo(CAB) = 2α, cuya tangente queda: tan(2α) = y/x.
Luego, observa que tienes:
Ángulo(CBA) = α, cuya tangente queda tanα = y/(3 - x).
Luego, sustituyes en la ecuación de la identidad trigonométrica y queda:
y/x = [ 2*y/(3 - x) ] / [ 1 - y2/(3 - x)2 ],
haces pasajes de divisores como factores y queda:
y*[ 1 - y2/(3 - x)2 ] = x*[ 2*y/(3 - x) ],
distribuyes en el primer miembro, resuelves el producto en el segundo miembro, y queda:
y - y3/(3 - x)2 = 2*x*y/(3- x),
multiplicas en todos los términos de la ecuación por (3 - x)2 y queda:
y*(3 - x)2 - y3 = 2*x*y*(3 - x),
desarrollas el primer término y el último término, y queda:
9*y - 6*x*y + x2*y = 6*x*y - 2*x2*y,
haces pasajes de términos y queda:
3*x2*y - 12*x*y + 9*y = 0,
divides en todos los términos por 3 y queda:
x2*y - 4*x*y + 3*y = 0,
extraes factor común y queda:
y*(x2 - 4*x + 3) = 0,
luego, por anulación de un producto, tienes dos opciones:
1°)
y = 0, que no corresponde a este problema (observa que los puntos A, B y C quedan todos sobre el eje OX, por lo que tienes que no determinan un triángulo);
2°)
x2 - 4*x + 3 = 0, que es una ecuación polinómica cuadrática cuyas soluciones son:
x = 1, y x = 3,
y observa que los puntos de la segunda recta no cumplen con la condición establecida en el enunciado, ya que para ellos tienes que el lado BC es vertical, por lo que el ángulo CBA es recto, y no tiene tangente trigonométria,
por lo que tienes que el lugar geométrico está formado por los puntos de la recta paralelas al eje OY cuya ecuación es:
x = 1,
Espero haberte ayudado.
Antonio Silvio Palmitano
el 8/9/1712)
Comienza por plantear la pendiente de lA recta que pasa por los puntos C y D:
mCD = (- 4 - 2)/(3 + 2) = - 6/5;
luego, como debes encontrar la ecuación de una recta paralela a ella que pasa por el punto A(7,8), tienes que las rectas tienen pendientes iguales, por lo que puedes plantear su ecuación cartesiana (punto-pendiente):
y - 8 = - (6/5)*(x - 7).
15)
Como tienes que el punto pertenece a la recta, reemplazas sus coordenadas en la ecuación y queda:
k*(-2) - 4 + 8 = 0,
reduces términos semejantes, haces pasaje de término y queda:
k*(-2) = - 4,
haces pasaje de factor como divisor y queda:
k = 2;
luego reemplazas en la ecuación del enunciado y queda
2*x - y + 8 = 0.
Espero haberte ayudado.
-
 hola me podéis explicar que ha hecho con el limite después del infinito/infinito porque no lo entiendo gracias.
hola me podéis explicar que ha hecho con el limite después del infinito/infinito porque no lo entiendo gracias.Antonio Silvio Palmitano
el 8/9/17Han aplicado la Regla de L'Hôpital (observa que han derivado independientemente al numerador y al denominador), para luego resolver:
Lím(x→0+) ( lnx / (1/x) ) = aplica la Regla de L'Hôpital = Lím(x→0+) ( (1/x) / (-1/x2) ) =
= Lím(x→0+) ( - x2/x ) = Lím(x→0+) ( - x ) = 0.
Espero haberte ayudado.
-
El tiempo de espera (en horas) de un pescador hasta pescar una trucha sigue una distribución exponencial de parámetro λ=2.
¿Cuál es la probabilidad de que al cabo de una hora aún no haya pescada ninguna trucha?
Antonio Silvio Palmitano
el 8/9/17Plantea la expresión de la función de distribución:
f(x) = 2*e-2*t, con t ≥ 0, t ∈ R.
Luego, plantea:
p(X > 1) = ∫ 2*e-2*t*dt = [ -e-2*t ], para evaluar entre 1 y +∞;
luego, y resumiendo el planteo para el límite impropio, resuelves y queda:
p(X > 1) = 0 - (- e-2*1) = e-2*1 = e-2 = 1/e2.
Espero haberte ayudado.
-
Demuestre que x-1 es un factor de un polinomio P de grado positivo si y sólo si la suma de los coeficientes de P es cero.
Antonio Silvio Palmitano
el 8/9/17Como tienes que x-1 es factor del polinomio, también tienes que 1 es raíz del polinomio.
Luego, plantea la expresión del polinomio:
P(x) = a0 + a1x + a2x2 + ... + anxn,
luego, plantea la condición de raíz para 1
P(1) = 0, evalúas en el primer miembro con la expresión del polinomio y queda:
a0 + a1(1) + a2(1)2 + ... + an(1)n = 0,
resuelves factores con bases numéricas (observa que todos son iguales a 1) y queda:
a0 + a1 + a2 + ... + an = 0.
Espero haberte ayudado.
-
Indica qué es el punto P(2,2) con respecto a la siguiente circunferencia:
Explicación
El centro es: C(5,0), por lo tanto el radio es:
Por lo tanto al ser menor que el radio, P es un punto interior a la circunferencia
¿Alguno de ustedes me puede explicar el ejercicio por favor?