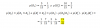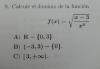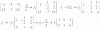-
No se como continuar este problema, si: a= a quiere decir que no tiene inversa? Y la segunda parte es sustituir el 2 en la a y sacar el determinante? Gracias.

Antonio Silvio Palmitano
el 6/9/17Observa que el determinante de la matriz queda:
|A| = (a + 3a + 0) - (0 + 0 + 3a) = 4a - 3a = a,
por lo que tienes que a debe ser distinto de cero para que la matriz A sea invertible.
Luego, tienes la matriz para a = 2:
A =
2 1 0
0 1 3
2 1 1
Luego, plantea la doble matriz (A-Identidad), a fin de aplicar el Método de Gauss para calcular A-1:
2 1 0 1 0 0
0 1 3 0 1 0
2 1 1 0 0 1
a la tercera fila le restas la primera fila, y queda:
2 1 0 1 0 0
0 1 3 0 1 0
0 0 1 -1 0 1
a la primera fila le restas la segunda fila y queda
2 0 -3 1 -1 0
0 1 3 0 1 0
0 0 1 -1 0 1
a la primera fila le sumas el triple de la tercera, a la segunda fila le restas el triple de la tercera, y queda:
2 0 0 -2 -1 3
0 1 0 3 1 -3
0 0 1 -1 0 1
a la primera fila la multiplicas por 1/2 y queda:
1 0 0 -1 -1/2 3/2
0 1 0 3 1 -3
0 0 1 -1 0 1
Luego, tienes remarcados a los elementos de la matriz inversa de la matriz A.
Espero haberte ayudado.
-
Desencadenado
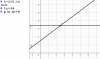
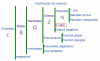
el 7/9/17Te hice uno como ejemplo. Debes ver hacia donde va la gráfica en el punto dado. Cuando tiene un menos sobre el número, significa que debes fijarte el gráfico que está a la izquierda del valor dado; y si tiene un más, el gráfico que debes tener en cuenta es el de la derecha. Espero te haya podido ayudar. Saludos!
-
Verónica Osorio Araujo
el 6/9/17Antonio Silvio Palmitano
el 6/9/17a)
Observa que la función f es diferenciable en R2, ya que sus derivadas parciales son continuas en R2, y las expresiones de sus derivadas parciales son:
fx = 2x + y, que evaluada en el punto de estudio queda: fx(2,1) = 2*2 + 1 = 5,
fy = x - 3, que evaluada en el punto de estudio queda: fy(2,1) = 2 - 3 = - 1;
luego, tienes la expresión del vector gradiente de la función evaluado en el punto de estudio:
∇f(2,1) = < 5 , -1 >.
Luego, observa que el módulo del vector que determina la dirección queda:
|u| = √( 12 + (-2)2 ) = √(5).
Luego, puedes aplicar el Teorema de la derivada direccional de una función diferenciable:
Duf(2,1) = (∇f(2,1) • u) /|u| = reemplazas y queda:
= (< 5 , -1 > • < 1 , -2 >) / √(5) = desarrollas el producto escalar en el numerador y queda:
= ( 5*1 - 1*(-2) ) / √(5) = resuelves el numerador y queda
= 7/√(5) = racionalizas el denominador y queda:
= 7√(5)/5.
Espero haberte ayudado.
Antonio Silvio Palmitano
el 6/9/17b)
Observa que la función es continua, con derivadas parciales primeras y segundas continuas en R2.
Luego, plantea las expresiones de las derivadas primeras:
fx = 3x2 - 3y
fy = - 3x + 2y.
Luego, plantea las expresiones de las derivadas segundas:
fxx = 6x
fxy = - 3
fyx = - 3
fyy = 2.
Luego, plantea la condición de punto estacionario (posible máximo o posible mínimo):
fx = 0
fy = 0,
sustituyes expresiones y queda:
3x2 - 3y = 0
- 3x + 2y = 0, de aquí despejas: y = (3/2)x (1),
luego sustituyes en la primera ecuación y queda:
3x2 - (9/2)x = 0, divides en todos los términos de la ecuación por 3 y queda:
x2 - (3/2)x = 0, que es una ecuación polinómica cuadrática cuyas soluciones son:
1)
x = 0, que al sustituir en la ecuación señalada (1) queda: y = 0, por lo que tienes el punto: A(0,0);
2)
x = 3/2, que al sustituir en la ecuación señalada (1) queda: y = 9/4, por lo que tienes el punto: B(3/2,9/4).
Luego, para cada punto estacionario evalúas las derivadas segundas:
1)
Para el punto A(0,0) tienes: fxx = 6*0 = 0, fxy = - 3, fyx = - 3, fyy = 2,
luego, evalúas el discriminante hessiano para este punto (H = fxx*fyy - fxy*fyx) y queda:
H(0,0) = 0*2 - (-3)*(-3) = 0 - 9 = - 9 < 0,
por lo que tienes, según el criterio de las derivadas segundas, que la gráfica de la función presenta un punto de ensilladura en A(0,0), y el valor de la función para este punto es: f(0,0) = 0.
2)
Para el punto B(3/2,9/4) tienes: fxx = 6*(3/2) = 9, fxy = - 3, fyx = - 3, fyy = 2,
luego, evalúas el discriminante hessiano para este punto (H = fxx*fyy - fxy*fyx) y queda:
H(3/2,9/4) = 9*2 - (-3)*(-3) = 18 - 9 = 9 > 0,
por lo que tienes, según el criterio de las derivadas segundas (observa que para este punto tienes:
fxx = 9 > 0), que la gráfica de la función presenta un mínimo local en B(3/2,9/4), y el valor de la función para este punto es:
f(3/2,9/4) = (3/2)3 - 3(3/2)(9/4) + (9/4)2 = 27/8 - 81/8 + 81/64 = - 351/64.
Espero haberte ayudado.
Verónica Osorio Araujo
el 6/9/17Antonio Silvio Palmitano
el 6/9/17Recuerda la expresión del módulo de un vector.
Si tienes el vector: u = < a , b >, entonces su módulo queda expresado:
|u| = √(a2 + b2).
Luego, tienes en tu enunciado que el vector dirección es: u = < 1 , -2 >,
luego reemplazas en la expresión (observa que tienes: a = 1 y b = -2) y queda:
|u| = √(a2 + b2) = √( (1)2 + (-2)2) = resuelves cuadrados = √(1 + 4) = resuelves el argumento = √(5).
Espero haberte ayudado.
-
Ángel
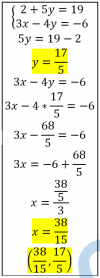
el 6/9/17(*) 2x+5y= 19
(**) 3x-4y= -6
Si multiplicamos (*) por 3 y (**) por -2 obtenemos:
6x+15y= 57
-6x+ 8y= 12
Al sumar las dos resulta que:
6x+15y= 57
-6x+ 8y= 12
--------------------
0x+23y=69
Despejando:
23y=69 ---------> y=3
Sustituimos en (*) el valor de y=3 para obtener el valor de x:
2x+5y=19 ------> 2x+ 5*3 =19 -------> 2x+15=19 -----> 2x=4 -----> x=2
Finalmente, obtenemos la matríz 1x2 (de una fila y dos columnas) con:
el elemento (1,1) con valor 2; que coincide con el de x
el elemento (1,2) con valor 3; que coincide con el de y
Solución: ( 2 3 )
-
ankhorey apolinario
el 6/9/17yo diría que la opción C ya que las raíces no pueden tener valores negativos y porque el resultado del denominador da 3, además las opciones a y b tienen números negativos así que no me cuadra, de todos modos no la he resuelto y te hablo un poco desde la ignorancia jajaja
Ángel
el 6/9/17x2 tiene que ser distinto de cero para que la fracción esté definida: x2≠0 ---> x≠0
(x-3)/x2 no puede ser negativo por estar dentro de la raíz-------> Como x2 es siempre positivo (teniendo en cuenta el anterior paso se descarta el x=0),
entonces el dominio de f(x) serán todos los x que cumplan x-3 ≥ 0 -------> x ≥ 3
Dom f(x)= [3,inf)
Antonio Silvio Palmitano
el 6/9/17Observa que en la expresión de la función tienes una raíz cuadrada (cuyo índice es 2, que es un número natural par), por lo que se impone que su argumento debe tomar valores mayores o iguales que cero:
(x - 3)/x2 ≥ 0 (1),
luego, observa que que la expresión (1) es fraccionaria, por lo que el denominador debe ser distinto de cero:
x2 ≠ 0, aquí haces pasaje de potencia como raíz, resuelves y queda: x ≠ 0 (2)
Luego, observa que el denominador de la expresión fraccionaria señalada (1) es estrictamente positivo (observa que es un cuadrado, y que ya hemos establecido que es distinto de cero), por lo que haces pasaje de divisor como factor (observa que no cambia la desigualdad y queda:
x - 3 ≥ 0, aquí haces pasaje de término y queda: x ≥ 3 (3).
Luego, observa que los elementos del intervalo D = [3,+∞):
- son distintos de cero, por lo que cumplen la condición señalada (2);
- son mayores o iguales que tres, por lo que cumplen la condición señalada (3);
- el argumento de la raíz cuadrada toma valores mayores o iguales que cero para todos ellos, por lo que cumplen la condición señalada (1);
luego, puedes concluir que la opción C es la respuesta correcta.
Espero haberte ayudado.
-
Hola me podrían ayudar con unas dudas?
1) ¿6/0 es un número No Real?
2) ¿0/6 a qué conjunto numérico pertenece?
3) ¿0 a qué conjunto numérico pertenece?
Antonio Silvio Palmitano
el 6/9/171)
La expresión escrita no corresponde a un número. Recuerda que en una expresión fraccionaria siempre debes terner un denominador distinto de cero.
2)
Tienes la expresión 0/6 que es igual a cero. Recuerda que si en una expresión fraccionaria tienes el numerador igual a cero y tienes el denominador distinto de cero, entonces la expresión es igual a cero
3)
El cero es un número muy particular, porque pertenece al conjunto de los números naturales, también pertenece al conjunto de los números enteros, también pertenece al conjunto de los números racionales, y también pertenece al conjunto de los números reales.
Espero haberte ayudado.
Ángel
el 6/9/171) Corresponde al concepto abstracto de "infinito" y hace referencia a una cantidad sin límite: es contrapuesto al (concepto) de finitud, que es implícito en el conjunto de los números; por lo que deducimos que no es un número.
2) y 3) Corresponde al número cero.
Observa que 0/1= 0/2= 0/3= 0/6= 0/1000= 0/n= 0