-
Bryam L Maldonado
el 14/7/17 -
MARCEL ALBERTO OLIVARES
el 14/7/17
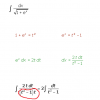
Hola buenas. Vengo con la intención de saber como desarrollar el siguiente problema (series de taylor). Determine la serie de Taylor en torno a x=0 de la función f(x) =xe2x . Utilice lo anterior para determinar el valor de ∑ ∞ n=1 (2 n-1 )/ 3 n+1 n!
Disculpen por no saber escribir bien la serie. Espero se entienda... Saludos y gracias de antemano!!
Antonio Silvio Palmitano
el 15/7/17Observa que la función tiene dominio R, y que es infinitamente derivable en R.
Luego, observa que su expresión puede escribirse:
f(x) = x*g(x) = (x - 0)*g(x).
Luego, recuerda el desarrollo en serie de Taylor en torno a x = 0 de la función:
g(u) = eu = ∑(k=0,∞) (1/k!)*uk,
luego haces el cambio de variable: u = 2x, y la expresión queda:
g(x) = e2x = ∑(k=0,∞) (1/k!)*(2x)k = ∑(k=0,∞) (2k/k!)*xk.
Luego sustituyes en la primera ecuación remarcada y queda:
f(x) = x*g(x) = x*∑(k=0,∞) (2k/k!)*xk = ∑(k=0,∞) (2k/k!)*xk+1.
Luego evalúas la sumatoria para x = 1/3 y queda:
f(1/3) = ∑(k=0,∞) (2k/k!)*(1/3)k+1 = ∑(k=0,∞) ( 2k / 3k+1*k! ) (1).
Luego evalúas la expresión de la función para x = 1/3) y queda:
f(1/3) = (1/3)*e2*(1/3)= e2/3/3 (2).
Luego igualas la expresión señalada (1) con el valor señalado (2) y queda:
∑(k=0,∞) ( 2k / 3k+1*k! ) = e2/3/3,
multiplicas y divides por 2 en el argumento de la sumatoria y queda:
∑(k=0,∞) ( 2*(2k/2) / 3k+1*k! ) = e2/3/3,
extraes el factor constante fuera de la sumatoria, resuelves la división de potencias con base 2 y queda:
2*∑(k=0,∞) ( 2k-1 / 3k+1*k! ) = e2/3/3,
haces pasaje de factor como divisor y queda:
∑(k=0,∞) ( 2k-1 / 3k+1*k! ) = e2/3/6,
extraes el primer término fuera de la sumatoria y queda:
20-1 / 30+1*0! + ∑(k=1,∞) ( 2k-1 / 3k+1*k! ) = e2/3/6,
resuelves el primer término en el primer miembro y queda:
1/6 + ∑(k=1,∞) ( 2k-1 / 3k+1*k! ) = e2/3/6,
haces pasaje de término y queda:
∑(k=1,∞) ( 2k-1 / 3k+1*k! ) = e2/3/6 - 1/6 = (e2/3 - 1)/6.
Espero haberte ayudado.
-
sandra rubio
el 14/7/17 -
Guillem De La Calle Vicente
el 14/7/17Sean A, B, C conjuntos arbitrarios incluidos en un universo U. Demuestra:
(Ac)c=A.
Antonio Silvio Palmitano
el 15/7/17Considera un elemento genérico perteneciente a (Ac)c.
x ∈ (Ac)c ↔ por definición de complemento de un conjunto:
↔ ∼ ( x ∈ (Ac) ) ↔ por definición de complemento de un conjunto:
↔ ∼ ( ∼ (x ∈ A) ) ↔ por equivalencia lógica:
↔ x ∈ A,
por lo tanto puedes concluir:
(Ac)c = A.
Espero haberte ayudado.
-
Edwin Ochoa
el 14/7/17 -
Bryam L Maldonado
el 14/7/17 -
Alejandro
el 14/7/17 -
Guillem De La Calle Vicente
el 14/7/17 -
Rafa Jiménez
el 14/7/17Buenas tardes. Podéis confirmarme si está bien planteado este problema:
Si el coeficiente medio de inteligencia de la población universitaria del colegio X es μ = 95 y σ =14, y se extrae una muestra de 49 estudiantes de esa población y el resultado de la media muestral es 98 y de la desviación típica muestral es 10. ¿Podemos concluir con un nivel de significación del 0,05 que la media poblacional es 95 ?
Contraste bilateral
Ho: μ = 95
H1 μ distinto a 95
Estadístico:
T= 98-95/10/(49)^0.5 = 2.1
Regla de aceptación (alfa = 0.05)
Co = (-zα/2 ; zα/2) = ( -1.96 ; 1.96) T no pertenece a Co por lo que se acepta H1
-
Andres William
el 14/7/17Buenos días,
Solicito el favor me colabore con este ejercicio.
De un paralelogramo se conoce un vértice, A(8, 0), y el punto de corte de las dos diagonales, Q(6, 2). También sabemos que otro vértice se encuentra en el origen de coordenadas. Calcular:
los otros vértices
Las ecuaciones de las diagonales
La longitud de las diagonales.
Muchas gracias por la ayuda.
