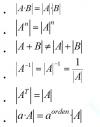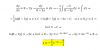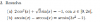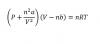http://www.vitutor.com/geo/vec/b_8.html 

https://es.symbolab.com/solver/step-by-step/2a%5E%7B3%7D%2B6a%5E%7B2%7D-8%3D0 

Tienes la ecuación polinómica cúbica:

2a³ + 6a² - 8 = 0, divides por 2 en todos los términos de la ecuación y queda:

a³ + 3a² - 4 = 0,

observa que no es factorizable en forma sencilla (recuerda que para factorizar, siempre debes tener 0 en el segundo miembro), por lo que debes investigar reemplazando valores hasta encontrar una solución.

Observa que a = 1 es una solución de la ecuación, por lo que aplicas la Regla de Ruffini (te dejo la tarea), y el primer miembro queda factorizado, por lo que la ecuación queda:

(a - 1)*(a² + 4a + 4) = 0,

factorizas el argumento del segundo agrupamiento (observa que es un trinomio cuadrado perfecto) y queda:

(a - 1)*(a + 2)² = 0,

luego, por anulación de un producto tienes dos opciones:

a - 1 = 0, de donde despejas a = 1 (que ya habíamos determinado),

(a + 2)² = 0, de donde despejas: a + 2 = 0, y luego despejas: a = - 2,

que son las dos soluciones de la ecuación del enunciado.

Espero haberte ayudado.

A·B=0 obliga a que A=0 o bien B=0.

Pero con A·B=8  no vale esto.

Muchísimas gracias!!!!

Puedes llamar x a la longitud de la base del rectángulo, y puedes llamar y a la longitud de su altura.

Luego, plantea para su perímetro:

2x + 2y = 23 m.

Luego, plantea para su superficie:

x*y = 19 m².

Luego, tienes el sistema de dos ecuaciones con dos incógnitas (cuyos valores deben ser estrictamente positivos,

porque son las longitudes de los lados del rectángulo):

2x + 2y = 23, de aquí despejas: 2y = 23 - 2x, y luego despejas: y = (23 - 2x)/2 (1)

x*y = 19,

luego sustituyes la expresión señalada (1) en la segunda ecuación y queda:

x*(23 - 2x)/2 = 19, haces pasaje de divisor como factor, distribuyes en el primer miembro, y queda:

23x - 2x² = 38, haces pasaje de término, ordenas términos y queda

- 2x² + 23x - 38 = 0, multiplicas por -1 en todos los términos de la ecuación y queda:

2x² - 23x + 38 = 0, que es una ecuación polinómica cuadrática cuyas soluciones son:

a) x = 19/2 = 9, 5 m, reemplazas en la ecuación señalada (1) y queda: y = (23 - 2(9,5))/2 = 4/2 = 2 m;

b) x = 2 m, reemplazas en la ecuación señalada (1) y queda y = (23 - 2(2)/2 = 19/2 = 9,5 m.

Luego, puedes concluir que los lados del rectángulo miden 2 m y 9,5 m.

Espero haberte ayudado.

Que ejercicio? no adjuntante nada :(

Solo se me ocurre el desarrollo de Taylor:

usando las propiedades de los determinantes:

tenemos:

det [ B5]=(det [B])5

det [At]=det [A]

det [5/9.C]=(5/9)3 det [C]

det [C-1]=1/det [C]

y

det[A·B]=det[A] · det[B]

por lo tanto:

det [ B5 . At .(5/9.C).C-1]=det [B5]·det [At]·det [(5/9.C]·det [C-1]=

=(det [B])5 · det [A] · (5/9)3 det [C] · 1/det [C] =

=b5·a·(5/9)3 c·1/c = (5/9)3 ab5

Haz el cambio:

t=√(1+e^x)

por lo que te quedaría:

e^x=t²-1 y dx=2t/(t²-1) dt

debes llegar a la integral de 2/(t²-1) que tendrás que resolver.

la solución sería:

ln|t-1| - ln|t+1| + C

y por lo tanto:

ln|√(1+e^x)-1| - ln|√(1+e^x)+1| + C

y en la (b) prueba arcsin+arccos=pi/2. Una identidad poco conocida pero util.

También tengo la demostración del seno de la diferencia por si la quieres ya que no me las se de memoria. Ah se me olvidó, las dos son válidas. No lo comprobé porque hace mucho que no hacía una de estas.

No te compliques la vida...