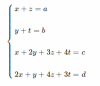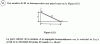-
Mario
el 10/7/17 -
Usuario eliminado
el 10/7/17¿Cómo podría resolver la ecuación: xx-1=e?
Necesito hallar sus 2 soluciones reales.
César
el 10/7/172. M´etodos generales para la resolucion de una ecuacion no lineal 21
2.1. El m´etodo de biparticion . . . . . . . . . . . . . . . . . . . . . . .
2 2.2. El m´etodo de aproximaciones sucesivas . . . . . . . . . . . . . .
. 27 2.2.1. La t´ecnica de sobreiteracion . . . . . . . . . . . . . . . . .
36 2.3. El m´etodo de Newton-Raphson . . . . . . . . . . . . . . . . . . .
37 2.4. Variantes del m´etodo de Newton-Raphson: m´etodos de la secante y de “regula falsi” . . . . . . . . . . . . . . . . . . . . . . . . . . .
51 2.4.1. M´etodo de la secante . . . . . . . . . . . . . . . . . . . . .
51 2.4.2. El metodo de “Regula Falsi” . . . . . . . . . . . . . . . . .
Ángel
el 10/7/17Por ahora las matemáticas no dan para conseguir un/unos valor/es exacto/s de x en este tipo de ecuaciónes, "sólo" buenas aproximaciones: http://www.ehu.eus/~mepmufov/html/Parte2.pdf
-
Guillermo
el 10/7/17 -
sara
el 10/7/17Hola, estoy haciendo un ejercicio de matrices y al resolver por el metodo de cramer me sale un resultado distinto al de mi profesor que lo resuelve por el metodo de gauss. Si alguien me pudiera decir si es porque estoy utilizando un metodo distinto, pero deberia salirme lo mismo asi que uno de los dos se equivoca...
El sistema es el siguiente:
ax + y + z = a
x - y + az = a
x + y + z = a
Antonius Benedictus
el 10/7/17 -
Guillem De La Calle Vicente
el 10/7/17Consideremos el sistema de ecuaciones lineales
Determinad qué condiciones tienen que cumplir los parámetros a, b, c, d a fin de que el sistema sea compatible determinado.
Antonius Benedictus
el 10/7/17 -
Guillem De La Calle Vicente
el 10/7/17Considera los siguientes conjuntos:
A={z∈ℕ: z²≤20∧∃x∈ℤ(z=2x)}
B={z∈ℤ: |z|<6∧∃x∈ℤ(|z|=x²)}
C={0,{0,4},{-1,1},4}
Encuentra A\B.
Antonius Benedictus
el 10/7/17
Antonius Benedictus
el 11/7/17 -
Stephanie Salazar
el 10/7/17 -
Princesa Leia
el 10/7/17
Hola, soy una estudiante de Ingeniería Química y me estoy preparando un examen de Matemáticas II cuya parte esencial es la integración múltiple y sus aplicaciones.
Tengo dos problemas de clase que el profesor apenas planteó y que no atino a resolver correctamente. Agradecería mucho que alguien me sacase de dudas ya que este tipo de problemas es típico de los exámenes y no consigo terminar de plantearlos.
El primero :
Volumen que se produce al girar alrededor del eje OY la región limitada por la parábola y=x^2-1 , el eje OX y la recta vertical x=2. El profesor nos planteó un cambio a coordenadas cilíndricas :
x=rcos (theta)
y=y
z=rsen(theta)
pero ni lo resolvió ni lo terminó de plantear
Le he estado dando vueltas y creo que el cambio a cilíndiricas no es del todo correcto, habría de ser x=1+rcos(theta) y así luego me quedaría 0<y<(1+rcos(theta))^2-1 para los límites de integración en la integral triple ( colocando también r entre 1 y 2 y el ángulo trheta entre 0 y 2pi. El resultado que obtengo es (15pi)/4, que me parece totalmente coherente.
Pero no estoy segura de estar haciendo lo correcto.
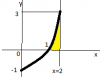
El segundo problema es prácticamente similar : volumen del cuerpo que engendra la región 1<x<2 y 0<y<x-1 al girar sobre el eje OY. El planteamiento lo hago similar al anterior, incluso poniendo también x=1+rcos(theta) porque la situación gráfica es similar al anterior problema. Pero obtengo cero de resultado, así que está mal y , además, me hace sospechar también del primero porque uso ahora en éste el mismo proceso.
Agradecería mucho que alguien me ayudase con ambos problemas, tengo el examen a finales de esta semana y estoy un poco agobiada con este tipo de problemas. Ojalá me podáis ayudar. Como digo, os estaré muy agradecida.
Antonius Benedictus
el 10/7/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
Antonio Silvio Palmitano
el 10/7/17
Disculpa los errores de escala en el gráfico de la imagen.
Observa que la región se parece a un triángulo con vértices: (1,0), (2,0) y (2,3),
que está limitado por un segmento de la recta cuya ecuación es x = 2 (que es su lado más alejado del eje de giros OY),
por un segmento de la parábola cuya ecuación es y = x2 - 1, de donde puedes despejar: +√(y+1) = x (que es su lado más cercano al eje de giros OY),
y por un segmento de eje OX que es su base:
Luego, recuerda la expresión del volumen de revolución alrededor del eje OY, expresado con una integral de una sola variable:
Vy = π ∫ ( f(y)2 - g(y)2 )*dy, con a ≤ y ≤ b,
donde x = f(y) es la ecuación del la curva que contiene al lado "más alejado" del eje de giro, y x = g(y) es la ecuación de la curva que contiene al lado "más cercano" al eje de giro, y donde a y b son las ordenadas de los puntos "más bajos" y "más altos" en el gráfico cartesiano, de la región que debes rotar.
Luego, para este ejercicio queda:
Vy = π ∫ ( 22 - ( √(y+1) )2 )*dy = π ∫ ( 4 - (y+1) )*dy = π ∫ ( 3 - y )*dy, para integrar en el intervalo 0 ≤ y ≤ 3 (te dejo la tarea).
Pero si debes emplear coordenadas cilíndricas con eje OY, debes comenzar por plantear la ecuación del paraboloide de revolución generado por la curva de ecuación y = x2 - 1, al rotar alrededor del eje OY:
y = x2 + z2 - 1, para luego expresarla en coordenadas cilíndricas de eje OY, haces las sustituciones y queda: y = r2 - 1;
luego, observa que los límites de integración quedan:
"y entre el plano OXZ y el paraboloide" que queda expresado: 0 ≤ y ≤ r2 - 1,
"r entre sus distancias mínima y máxima al eje de giros OY", que queda expresado: 1 ≤ r ≤ 2,
"todo alrededor del eje de giros OY", que queda expresado: 0 ≤ θ ≤ 2π;
luego, el volumen de revolución alrededor del eje OY queda expresado como una integral triple (recuerda el factor de compensación, o Jacobiano: |J| = r):
Vy = ∫∫∫ r*dy*dr*dθ, con los límites de integración que hemos indicado (te dejo la tarea de resolver la integral).
Espero haberte ayudado.
Antonio Silvio Palmitano
el 10/7/17
El planteo es muy similar al ejercicio anterior, tal como dices, y es mucho más práctico calcular el volumen de revolución alrededor del eje OY con una integral de una sola variable, para lo que tienes:
x = 2, de donde tienes para sustituir: f(y) = 2,
y = x - 1, de donde despejas: y + 1 = x, y tienes para sustituir: g(y) = y + 1,
todo para integrar en el intervalo 0 ≤ y ≤ 1.
Pero si debes emplear coordenadas cilíndricas de eje OY, observa que el sólido está limitado por un cilindro circular de eje OY y radio 2, cuya ecuación cartesiana es:
x2 + z2 = 4, que al sustituir queda: r2 = 4, de donde despejas: r = 2,
y un semicono con eje OY y vértice en el punto V(0,-1,0) cuya ecuación cartesiana es:
x2 + z2 = (y + 1)2, que al sustituir queda: r2 = (y + 1)2, haces pasaje de potencia como raíz y queda: r = y + 1de donde despejas: r - 1 = y:
luego, para los límites de integración, tienes:
"y entre el plano OXZ y el cono", que queda expresado: 0 ≤ y ≤ r - 1,
"r entre sus distancias mínima y máxima al eje de giro OY", que queda expresado: 1 ≤ r ≤ 2,
"todo alrededor del eje de giro OY", que queda expresado: 0 ≤ θ ≤ 2π.
Luego puedes continuara la tarea.
Espero haberte ayudado.
-
Stephanie Salazar
el 10/7/17 -
Stephanie Salazar
el 10/7/17Encontrar dos números positivos cuyo producto sea 20 y la suma de sus cuadrados sea mínima
Alejandro Legaspe
el 10/7/17Sabemos que si el producto es 20, ent
xy=20
La suma de sus cuadrados sea minima
x²+y²=A
La funcion A es la que hay que minizar, sabemos que y=20/x por la primera ecuacion,ent A nos queda
A=x²+(20/x)²=x²+400/x²
Si obtenemos la derivada de A,ent
A'=2x+400(-2)/x³=2x-800/x³
Veamos cuando A'=0
2x-800/x³=0
2x4-800=0
2x4=800
x4=800/2=400
x=±2√5, como x>0, al ser un numero positivo, ent x=2√5
Ve que si tomamos una x entre 0 y 2√5 A'(x)<0 luego A(x) es decreciente, si tomamos una x superior a 2√5 , A'(x)>0, luego A(x) es creciente, es decir en x=2√5 hay un minimo
Luego como y=20/x=20/2√5=10/√5=10√5/5=2√5
Nos cuentas si hay mas dudas
