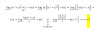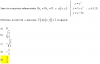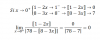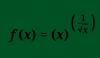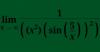-
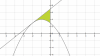
Me piden hallar el área limitada por la parábola y= -x^2 -2x+3 y su tangente en el punto (-2,3) y el eje y.
¿Como puedo hacer este ejercicio? Muchas gracias.
Antonio Silvio Palmitano
el 2/7/17Observa que la gráfica de la parábola corta al eje OX en los puntos cuyas coordenadas son (-3,0) y (1,0),
que su vértice (máximo) es el punto de coordenadas (-1,4), y que corta al eje OY en el punto de coordenadas (0,3).
Luego plantea la expresión de la función derivada primera, a partir de la expresión de la parábola:
y ' = - 2x - 2, luego evalúas para la abscisa del punto que es dato en el enunciado, y tienes la pendiente de la recta tangente:
m = -2*(-2) - 2 = 4 - 2 = 2,
luego plantea la ecuación cartesiana de la recta tangente a la curva que pasa por el punto dato:
y - 3 = 2( x - (-2) ), distribuyes en el segundo miembro y queda:
y - 3 = 2x + 4, haces pasaje de término y queda:
y = 2x + 7,
luego, observa que la recta tangente corta al eje OY en el punto cuyas coordenadas son (0,7).
Luego, tienes que la región a la que debes calcular su área (haz un gráfico) está limitada por:
la recta tangente (superiormente), la parábola (inferiormente) y el eje OY lateralmente por la derecha,
y observa que la región tiene tres vértices: (-2,3), (0.3) y (0,7).
Luego, puedes plantear para el área de la región:
A = ∫ ( (2x+7) - (-x2-2x+3) ) dx = ∫ (2x + 7 + x2 + 2x - 3) dx = ∫ (x2 + 4x + 4) dx, para evaluar con la Regla de Barrow entre x = - 2 y x = 0,
integras término a término y queda:
A = [ x3/3 + 2x2 + 4x ] = evalúas = (0 + 0 + 0) - (- 8/3 + 8 - 8) = 0 - (-8/3) = 8/3.
Espero haberte ayudado.
-
Buenos días. Me podes ayudar con esta integral. No entiendo como se ha llegado al resultado. Gracias.
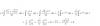
Antonio Silvio Palmitano
el 2/7/17Tienes el argumento de la integral:
f(x) = ( ∛(x) + √(5*x3) ) / (3*x), distribuyes la raíz cuadrada en el numerador y queda:
f(x) = ( ∛(x) + √(5)*√(x3) ) / (3*x),
escribes las raíces cuyas bases son literales como potencias con exponentes fraccionarios y queda:
f(x) = ( x1/3 + √(5)*x3/2 ) / (3*x), distribuyes el denominador y queda:
f(x) = x1/3 / (3*x) + √(5)*x3/2 ) / (3*x), aplicas la propiedad de la división de potencias con bases iguales en ambos términos y queda:
f(x) = x-2/3/3 + √(5)*x1/2 /3, ordenas factores y queda:
f(x) = (1/3)*x-2/3 + ( √(5)/3 )*x1/2.
Luego integras término a término y queda la última línea del desarrollo que enviaste en tu imagen.
Espero haberte ayudado.
-
Hola amigos necesito ayuda con el problema que se los adjunto en la imagen. Por favor necesito ayuda.
Antes una aclaracion Ap(x) es el conjunto de verdad, y N[Ap(x)] es la cardinalidad de dicho conjunto.
Gracias de antemano. Bye y saludos
-
Una matriz mágica es una matriz cuadrada en qué todas las filas, columnas y las dos diagonales suman un cierto valor σ.
Probad que, dados (a,b,c)∈ℛ³, existe una única matriz mágica M(a,b,c)∈M3x3(ℛ) tal que
m22=a, m11=a+b, m13=a+c.
con mji, j es el elemento de la fila y i el elemento de la columna. -
Sea x∈ℕ. Identifica qué propiedades del número x describe la siguiente expresión, es decir, qué conjuntos de números naturales definen cuándo escribimos {x∈ℕ:...}.
¬∃p,q∈ℕ(p≠1∧q≠1∧x=p·q)
Guillem De La Calle Vicente
el 5/7/17 -
Una persona que pesa 80 Kg se encuentra sobre una plataforma cuyo peso es 40 Kg. La persona tira de una cuerda atada a la plataforma y que pasa por una polea fijada al techo. ¿Que fuerza debe ejercer para darse a si mismo y a la plataforma una aceleracion de 0.6m/seg^2?
Alejandro Legaspe
el 2/7/17Habra que analizar las fuerzas en el eje vertical, y hay dos, a saber, el peso del sistema, que va hacia abajo (la persona y la plataforma) y la tension que ofrece la cuerda y esta fuerza va hacia arriba
Calculemos el peso del sistema, sumando ambas masas, tenemos que la masa del sistema es de 120kg, por lo tanto, el peso es de P=120(9,8)
Por la segunda ley de Newton, sabemos que la suma de las fuerzas es igual a masa por aceleracion, luego si aplicamos esto en el eje vertical tenemos que la suma del peso y de la tension (que al ir en sentidos diferentes se restaran) es igual a la masa del sistema por la aceleracion, i.e.
F-P=ma ; donde F es la fuerza de tension
,luego F=P+ma=mg+ma=m(g+a)=120kg(9,8m/s2+0,6m/s2)=120kg(10,4m/s2) =1248N
Si tienes alguna duda, nos cuentas
Luis Alfredo Pinto
el 2/7/17Francisco Gutiérrez Mora
el 2/7/17 -
Buenas!
Necesito de su ayuda unicoos!
Me e encontrado este par de ejercicios que no encuentro su solución!
Del f(x) necesito la segunda derivada.